Introduction
This documentation will show the complete procedure for analyzing two-group data. For profiling, differential expression, enrichment, and network analysis, we use data from the study “Adipose tissue ATGL modifies the cardiac lipidome in pressure-overload-induced left ventricular failure” (Salatzki et al. 2018) as an example. For machine learning, we use data from the study “The landscape of cancer cell line metabolism” (Li et al. 2019) due to the sample size limitations.
Installation
Here is the procedures of running the LipidSigR package on your system. We assume that you have already installed the R program (see the R project at http://www.r-project.org and are familiar with it. You need to have R 4.3.0 or a later version installed for running LipidSigR.
Our package is available at the github https://github.com/BioinfOMICS/LipidSigR. Following are the instructions for installing our package.
# Step 1: Install devtools
install.packages("devtools")
# Step 2: Install BiocManager
if (!require("BiocManager", quietly = TRUE))
install.packages("BiocManager")
# Step 3: Install LipidSigR
## Update repositories
options(repos = c(
CRAN = "https://cloud.r-project.org/",
BiocManager::repositories()))
## Install dependencies and package
devtools::install_github(
"BioinfOMICS/LipidSigR",
dependencies = TRUE)LipidSigR relies on several dependencies. If an error indicates a missing package, you can install the required packages using the commands below.
# LipidSigR package depends on several packages, which can be installed using the below commands:
BiocManager::install(
c('fgsea', 'gatom', 'mixOmics', 'S4Vectors', 'BiocGenerics',
'SummarizedExperiment', 'rgoslin'))
install.packages(
c('devtools', 'magrittr', 'plotly', 'tidyverse', 'factoextra', 'ggthemes',
'ggforce', 'Hmisc', 'heatmaply', 'hwordcloud', 'iheatmapr', 'Rtsne', 'uwot',
'wordcloud', 'rsample', 'ranger', 'caret', 'yardstick', 'fastshap',
'SHAPforxgboost', 'visNetwork', 'tidygraph', 'ggraph'))
devtools::install_github("ctlab/mwcsr")After the installation, you can load and start using our package!
Data preparation
The input data of our functions must be a SummarizedExperiment object
construct by as_summarized_experiment or output from
upstream analysis function.
Input data for general analysis
For profiling, differential expression, enrichment, and network analysis, we use data from the study “Adipose tissue ATGL modifies the cardiac lipidome in pressure-overload-induced left ventricular failure” (Salatzki et al. 2018) as an example dataset. The human plasma lipidome of 10 healthy controls and 13 patients with systolic heart failure (HFrEF) was analyzed using MS-based shotgun lipidomics. Through the steps below, you can construct the input SummarizedExperiment object. NOTE: For constructing the input data for machine learning analysis and correlation analysis, please refer to the corresponding section (Input data for machine learning and Input data for correlation).
Input data frames
The abundance data and group information table must be provided as data frames and adhere to the following requirements.
Abundance data: The lipid abundance data includes the abundance values of each feature across all samples.
- The first column of abundance data must contain a list of lipid names (features).
- Each lipid name (feature) is unique.
- All abundance values are numeric.
For example:
rm(list = ls())
data("abundance_twoGroup")
head(abundance_twoGroup[, 1:6], 5)
#> feature control_01 control_02 control_03 control_04 control_05
#> 1 Cer 38:1;2 0.1167960 0.1638070 0.1759450 0.1446540 0.172092
#> 2 Cer 40:1;2 0.7857833 0.9366095 0.8944465 0.8961396 1.056512
#> 3 Cer 40:2;2 0.1494030 0.1568970 0.1909800 0.1312440 0.248504
#> 4 Cer 42:1;2 1.8530153 2.1946591 2.6377576 2.3418783 2.143355
#> 5 Cer 42:2;2 1.3325520 1.2514943 1.9466750 1.2948319 1.634636Group information table: The group information table contains the grouping details corresponding to the samples in lipid abundance data.
- The column names are arranged in order of sample_name, label_name, group, and pair.
- All sample names are unique.
- Sample names in ‘sample_name’ column are as same as the sample names in lipid abundance data.
- Columns of ‘sample_name’, ‘label_name’, and ‘group’ columns do not contain NA values.
- The column ‘group’ contain 2 groups.
- In the ‘pair’ column for paired data, each pair must be sequentially numbered from 1 to N, ensuring no missing, blank, or skipped numbers are missing; otherwise, the value should be all marked as NA.
For example:
Mapping lipid characteristics
The purpose of this step is to exclude lipid features not recognized
by rgoslin package. Please follow the instructions below
before constructing the input data as a SummarizedExperiment object.
- In this step, an error message will be returned if
rgoslin::parseLipidNamescannot recognize a certain lipid. However, if your data contains at least two recognizable lipids, it will be sufficient for analysis (note that different analyses may have varying data requirements).
library(dplyr)
# map lipid characteristics by rgoslin
parse_lipid <- rgoslin::parseLipidNames(lipidNames=abundance_twoGroup$feature)
#> Encountered an error while parsing 'SE 27:1;0-14:0;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'SE 27:1;0-15:0;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'SE 27:1;0-16:0;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'SE 27:1;0-16:1;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'SE 27:1;0-17:0;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'SE 27:1;0-17:1;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'SE 27:1;0-18:1;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'SE 27:1;0-18:2;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'SE 27:1;0-18:3;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'SE 27:1;0-19:2;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'SE 27:1;0-19:3;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'SE 27:1;0-20:2;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'SE 27:1;0-20:4;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'SE 27:1;0-20:5;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'SE 27:1;0-22:6;0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'ST 27:1;0': Expecting a single string value: [type=character; extent=4].
# filter lipid recognized by rgoslin
recognized_lipid <- parse_lipid$Original.Name[
which(parse_lipid$Grammar != 'NOT_PARSEABLE')]
abundance <- abundance_twoGroup %>%
dplyr::filter(feature %in% recognized_lipid)
goslin_annotation <- parse_lipid %>%
dplyr::filter(Original.Name %in% recognized_lipid)After running the above code, two data frames,
abundance, and goslin_annotation, will be
generated and used in the next step.
head(abundance[, 1:6], 5)
#> feature control_01 control_02 control_03 control_04 control_05
#> 1 Cer 38:1;2 0.1167960 0.1638070 0.1759450 0.1446540 0.172092
#> 2 Cer 40:1;2 0.7857833 0.9366095 0.8944465 0.8961396 1.056512
#> 3 Cer 40:2;2 0.1494030 0.1568970 0.1909800 0.1312440 0.248504
#> 4 Cer 42:1;2 1.8530153 2.1946591 2.6377576 2.3418783 2.143355
#> 5 Cer 42:2;2 1.3325520 1.2514943 1.9466750 1.2948319 1.634636
head(goslin_annotation[, 1:6], 5)
#> Normalized.Name Original.Name Grammar Message Adduct Adduct.Charge
#> 1 Cer 38:1;O2 Cer 38:1;2 Goslin NA NA 0
#> 2 Cer 40:1;O2 Cer 40:1;2 Goslin NA NA 0
#> 3 Cer 40:2;O2 Cer 40:2;2 Goslin NA NA 0
#> 4 Cer 42:1;O2 Cer 42:1;2 Goslin NA NA 0
#> 5 Cer 42:2;O2 Cer 42:2;2 Goslin NA NA 0Construct SE object
se <- as_summarized_experiment(
abundance, goslin_annotation, group_info=group_info_twoGroup,
se_type='de_two', paired_sample=FALSE)
#> Input data info
#> se_type: de_two
#> Number of lipids (features) available for analysis: 192
#> Number of samples: 23
#> Number of group: 2
#> Not paired samples.After running the above code, you are ready to begin the analysis
with the output se. After the code execution, a summary of
the input data will be displayed.
(Note: If errors occur during execution, please revise the input data to resolve them.)
Four main analysis workflows—“Profiling,” “Differential Expression,” “Enrichment,” and “Network”—can be conducted for two-group data.
“Profiling” provides an overview of comprehensive analyses to efficiently examine data quality, the clustering of samples, the correlation between lipid species, and the composition of lipid characteristics.
“Differential expression” integrates many useful lipid-focused analyses for identifying significant lipid species or lipid characteristics.
“Enrichment” provides two main approaches: ‘Over Representation Analysis (ORA)’ and ‘Lipid Set Enrichment Analysis (LSEA)’ to illustrates significant lipid species enriched in the categories of lipid class and determine whether an a priori-defined set of lipids shows statistically significant, concordant differences between two biological states (e.g., phenotypes).
“Network” provides functions for generates input table for constructing pathway activity network, lipid reaction network and GATOM network.
Please refer to the corresponding section for detailed descriptions and instructions.
Input data for machine learning
The data must include at least 60 samples for machine learning analysis, and the group information table format differs from other analyses. For these reasons, we use data from the study “The landscape of cancer cell line metabolism” here, where cancer cell lines are evenly divided into groups sensitive or resistant to SCD gene knockout based on gene dependency scores (CERES) (Li et al. 2019). This dataset consists of Group 0 (N = 114) and Group 1 (N = 114).
The input data of our functions must be a SummarizedExperiment object
construct by LipidSigR::as_summarized_experiment and after
being processed by LipidSigR::data_process.
Input data frames
The abundance data and group information table must be provided as data frames and adhere to the following requirements.
Abundance data: The lipid abundance data includes the abundance values of each feature across all samples.
- The first column of abundance data must contain a list of lipid names (features).
- Each lipid name (feature) is unique.
- All abundance values are numeric.
For example:
data("ml_abundance")
head(ml_abundance[, 1:6], 5)
#> # A tibble: 5 × 6
#> feature ACH_000973 ACH_000070 ACH_000411 ACH_001306 ACH_000137
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 LPC 14:0 6.07 5.99 5.81 5.69 5.91
#> 2 LPC 16:1 6.07 5.74 5.85 5.61 5.81
#> 3 LPC 16:0 6.08 5.59 5.81 5.58 6.10
#> 4 LPC 18:2 5.46 5.99 6.08 6.01 5.55
#> 5 LPC 18:1 6.18 5.49 5.93 5.67 5.96Group information table: The group information table contains the grouping details corresponding to the samples in lipid abundance data.
- The column names must be arranged in order of ‘sample_name’ and ‘group’.
- Sample names ‘sample_name’ column must be as same as the sample names in lipid abundance data.
- The column ‘group’ must be numeric (only be 0 or 1).
- Each group must have more than 30 samples.
For example:
Mapping lipid characteristics
The purpose of this step is to exclude lipid features not recognized
by rgoslin package. Please follow the instructions below
before constructing the input data as a SummarizedExperiment object.
- In this step, an error message will be returned if
rgoslin::parseLipidNamescannot recognize a certain lipid. However, if your data contains at least two recognizable lipids, it will be sufficient for analysis (note that different analyses may have varying data requirements).
library(dplyr)
# map lipid characteristics by rgoslin
parse_lipid <- rgoslin::parseLipidNames(lipidNames=ml_abundance$feature)
# filter lipid recognized by rgoslin
recognized_lipid <- parse_lipid$Original.Name[
which(parse_lipid$Grammar != 'NOT_PARSEABLE')]
abundance <- ml_abundance %>%
dplyr::filter(feature %in% recognized_lipid)
goslin_annotation <- parse_lipid %>%
dplyr::filter(Original.Name %in% recognized_lipid)After running the above code, two data frames,
abundance, and goslin_annotation, will be
generated and used in the next step.
head(abundance[, 1:6], 5)
#> # A tibble: 5 × 6
#> feature ACH_000973 ACH_000070 ACH_000411 ACH_001306 ACH_000137
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 LPC 14:0 6.07 5.99 5.81 5.69 5.91
#> 2 LPC 16:1 6.07 5.74 5.85 5.61 5.81
#> 3 LPC 16:0 6.08 5.59 5.81 5.58 6.10
#> 4 LPC 18:2 5.46 5.99 6.08 6.01 5.55
#> 5 LPC 18:1 6.18 5.49 5.93 5.67 5.96
head(goslin_annotation[, 1:6], 5)
#> Normalized.Name Original.Name Grammar Message Adduct Adduct.Charge
#> 1 LPC 14:0 LPC 14:0 Shorthand2020 NA NA 0
#> 2 LPC 16:1 LPC 16:1 Shorthand2020 NA NA 0
#> 3 LPC 16:0 LPC 16:0 Shorthand2020 NA NA 0
#> 4 LPC 18:2 LPC 18:2 Shorthand2020 NA NA 0
#> 5 LPC 18:1 LPC 18:1 Shorthand2020 NA NA 0Construct SE object
ml_input <- as_summarized_experiment(
abundance, goslin_annotation, group_info=condition_table,
se_type='ml', paired_sample=NULL)
#> Input data info
#> se_type: ml
#> Number of lipids (features) available for analysis: 88
#> Number of samples: 228
#> Number of group: 2
#> Not paired samples.After running the above code, you are ready to begin the analysis
with the output se. After the code execution, a summary of
the input data will be displayed.
(Note: If errors occur during execution, please revise the input data to resolve them.)
Input data for correlation
In the correlation workflow, we use data from the study “Plasma sphingolipids associated with chronic obstructive pulmonary disease phenotypes”, which identified strong associations between sphingomyelins and emphysema and between glycosphingolipids and COPD exacerbations (Bowler et al. 2015).
This dataset consists of 129 samples.
The input data of our functions must be a SummarizedExperiment object
construct by LipidSigR::as_summarized_experiment and after
being processed by LipidSigR::data_process.
Input data frames
The abundance data and group information table must be provided as data frames and adhere to the following requirements.
Abundance data: The lipid abundance data includes the abundance values of each feature across all samples.
- The first column of abundance data must contain a list of lipid names (features).
- Each lipid name (feature) is unique.
- All abundance values are numeric.
For example:
data("corr_abundance")
head(corr_abundance[, 1:6], 5)
#> # A tibble: 5 × 6
#> feature sample1 sample2 sample3 sample4 sample5
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 SM d18:1/14:1 1.44 1.36 1.03 0.398 1.14
#> 2 SM d18:1/14:0 1.09 0.934 1.02 0.519 1.27
#> 3 SM d18:1/16:1 1.14 0.898 1.03 0.695 1.23
#> 4 SM d18:1/16:0 0.883 0.875 0.952 0.778 1.16
#> 5 SM d18:1/18:1 1.18 1.06 0.838 0.923 1.08Group information table: The group information table includes various clinical attributes, including age, sex, BMI, clinical sub-phenotypes of COPD, symptoms, etc.
- The first column name must be ‘sample_name’.
- Sample names ‘sample_name’ column must be as same as the sample names in lipid abundance data.
- The column ‘sample_name’ must contain character values.
- Must include at least two columns containing numeric values (except ‘sample_name’ column).
For example:
data("corr_group_info")
head(corr_group_info[, 1:6], 5)
#> # A tibble: 5 × 6
#> sample_name FEV1_FVC Emphysema Exacerbations Age Sex
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 sample1 0.29 11.0 6 48.7 0
#> 2 sample2 0.57 2.36 0 70.1 0
#> 3 sample3 0.79 0.983 0 49.6 0
#> 4 sample4 0.39 35.0 0 54.1 1
#> 5 sample5 0.37 26.8 0 70.5 0Mapping lipid characteristics
The purpose of this step is to exclude lipid features not recognized
by rgoslin package. Please follow the instructions below
before constructing the input data as a SummarizedExperiment object.
- In this step, an error message will be returned if
rgoslin::parseLipidNamescannot recognize a certain lipid. However, if your data contains at least two recognizable lipids, it will be sufficient for analysis (note that different analyses may have varying data requirements).
library(dplyr)
# map lipid characteristics by rgoslin
parse_lipid <- rgoslin::parseLipidNames(lipidNames=corr_abundance$feature)
#> Encountered an error while parsing 'Sphingosine': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'Sphinganine': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'Sphingosine-1-phosphate': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'Sphinganine-1-phosphate': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'Hexosylsphingosine': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'HexCer d18:1/16:0;O': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'HexCer d18:1/18:0;O': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'HexCer d18:1/20:0;O': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'HexCer d18:1/22:0;O': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'HexCer d18:1/24:0;O': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'Hex2Cer d18:1/16:0;O': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'Hex2Cer d18:1/18:0;O': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'GM2 d18:1/16:0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'GM2 d18:1/18:0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'GD1 d18:1/16:0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'GD1 d18:1/18:0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'GD1 d18:1/20:0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'GQ1 d18:1/18:0': Expecting a single string value: [type=character; extent=4].
#> Encountered an error while parsing 'GQ1 d18:1/20:0': Expecting a single string value: [type=character; extent=4].
# filter lipid recognized by rgoslin
recognized_lipid <- parse_lipid$Original.Name[
which(parse_lipid$Grammar != 'NOT_PARSEABLE')]
abundance <- corr_abundance %>%
dplyr::filter(feature %in% recognized_lipid)
goslin_annotation <- parse_lipid %>%
dplyr::filter(Original.Name %in% recognized_lipid)After running the above code, two data frames,
abundance, and goslin_annotation, will be
generated and used in the next step.
head(abundance[, 1:6], 5)
#> # A tibble: 5 × 6
#> feature sample1 sample2 sample3 sample4 sample5
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 SM d18:1/14:1 1.44 1.36 1.03 0.398 1.14
#> 2 SM d18:1/14:0 1.09 0.934 1.02 0.519 1.27
#> 3 SM d18:1/16:1 1.14 0.898 1.03 0.695 1.23
#> 4 SM d18:1/16:0 0.883 0.875 0.952 0.778 1.16
#> 5 SM d18:1/18:1 1.18 1.06 0.838 0.923 1.08
head(goslin_annotation[, 1:6], 5)
#> Normalized.Name Original.Name Grammar Message Adduct Adduct.Charge
#> 1 SM 18:1;O2/14:1 SM d18:1/14:1 Goslin NA NA 0
#> 2 SM 18:1;O2/14:0 SM d18:1/14:0 Goslin NA NA 0
#> 3 SM 18:1;O2/16:1 SM d18:1/16:1 Goslin NA NA 0
#> 4 SM 18:1;O2/16:0 SM d18:1/16:0 Goslin NA NA 0
#> 5 SM 18:1;O2/18:1 SM d18:1/18:1 Goslin NA NA 0Construct SE object
corr_input <- as_summarized_experiment(
abundance, goslin_annotation, group_info=corr_group_info,
se_type='corr', paired_sample=NULL)
#> Input data info
#> se_type: corr
#> Number of lipids (features) available for analysis: 50
#> Number of samples: 129After running the above code, you are ready to begin the analysis
with the output se. After the code execution, a summary of
the input data will be displayed.
(Note: If errors occur during execution, please revise the input data to resolve them.)
Profiling
The first step in analyzing lipid data is to take an overview of the data. In this section, you can get comprehensive analyses to explore the quality and clustering of samples, the correlation between lipids and samples, and the abundance and composition of lipids.
Cross-sample variability
Now, let’s start with a simple view of sample variability to compare
the amount/abundance difference of lipid between samples (i.e., patients
vs. control). We will use the se conducted in the previous
section as the input data.
# conduct profiling
result <- cross_sample_variability(se)
# result summary
summary(result)
#> Length Class Mode
#> interactive_lipid_number_barPlot 8 plotly list
#> interactive_lipid_amount_barPlot 8 plotly list
#> interactive_lipid_distribution 8 plotly list
#> static_lipid_number_barPlot 9 gg list
#> static_lipid_amount_barPlot 9 gg list
#> static_lipid_distribution 9 gg list
#> table_total_lipid 3 data.frame list
#> table_lipid_distribution 3 data.frame listAfter running the above code, you will obtain a list called
result, containing interactive plots, static plots, and
tables for three types of distribution plots. (Note: Only static
plots are displayed here.)
# view result: histogram of lipid numbers
result$static_lipid_number_barPlot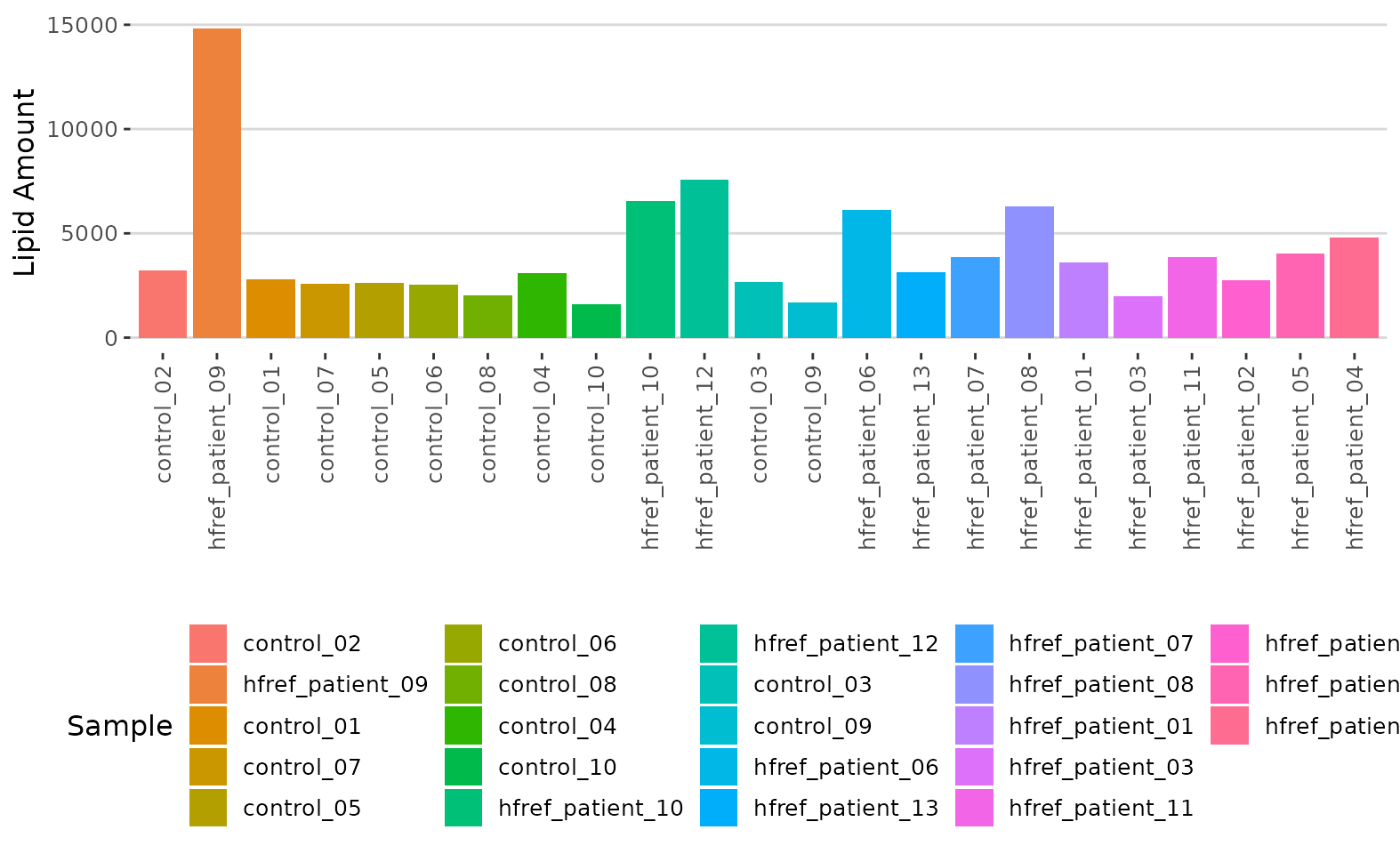
Histogram of lipid numbers The histogram overviews the total number of lipid species over samples. From the plot, we can discover the number of lipid species present in each sample.
# view result: histogram of the total amount of lipid in each sample.
result$static_lipid_amount_barPlot 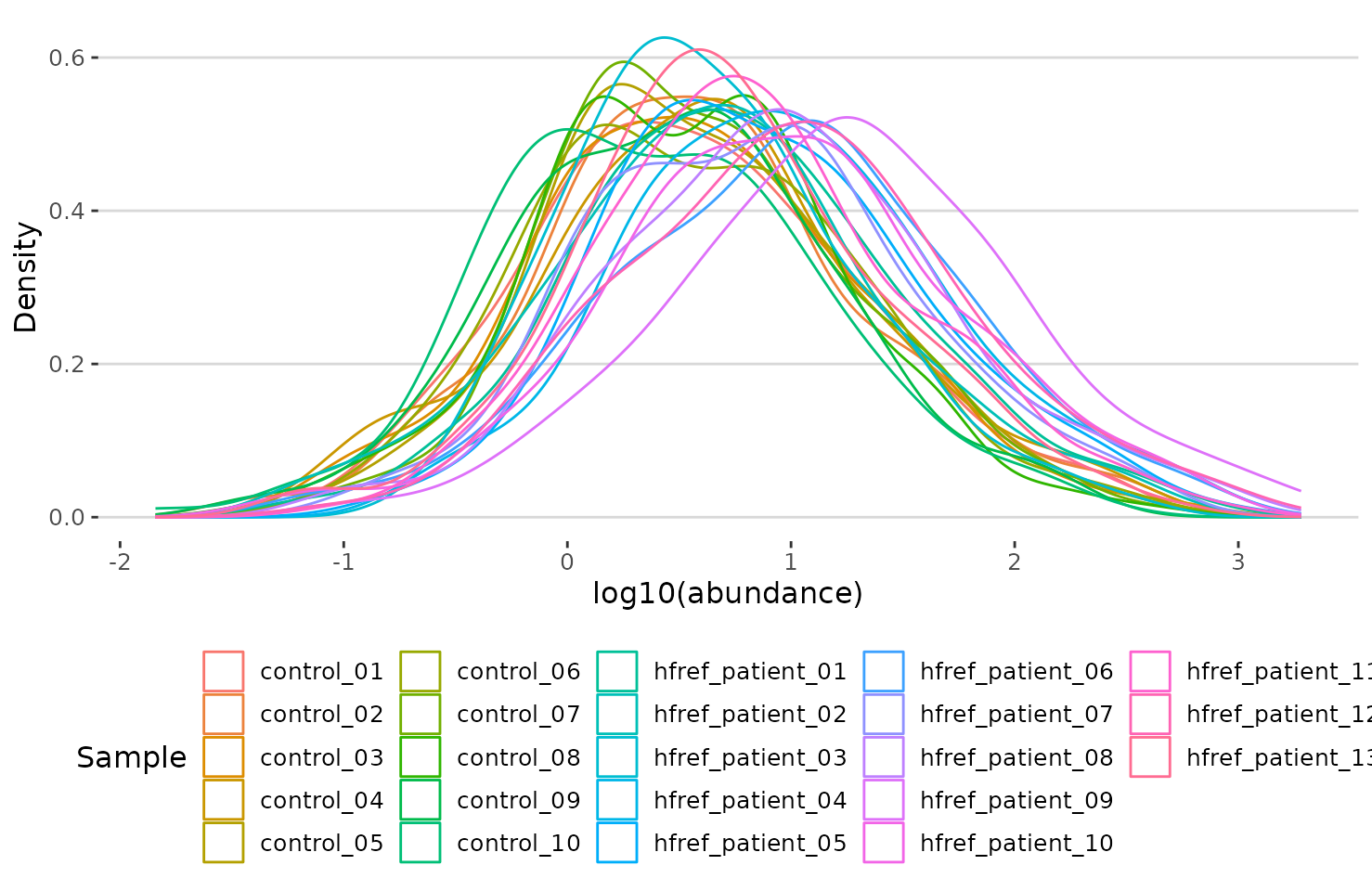
Histogram of lipid amount The histogram describes the variability of the total lipid amount between samples.
# view result: density plot of the underlying probability distribution
result$static_lipid_distribution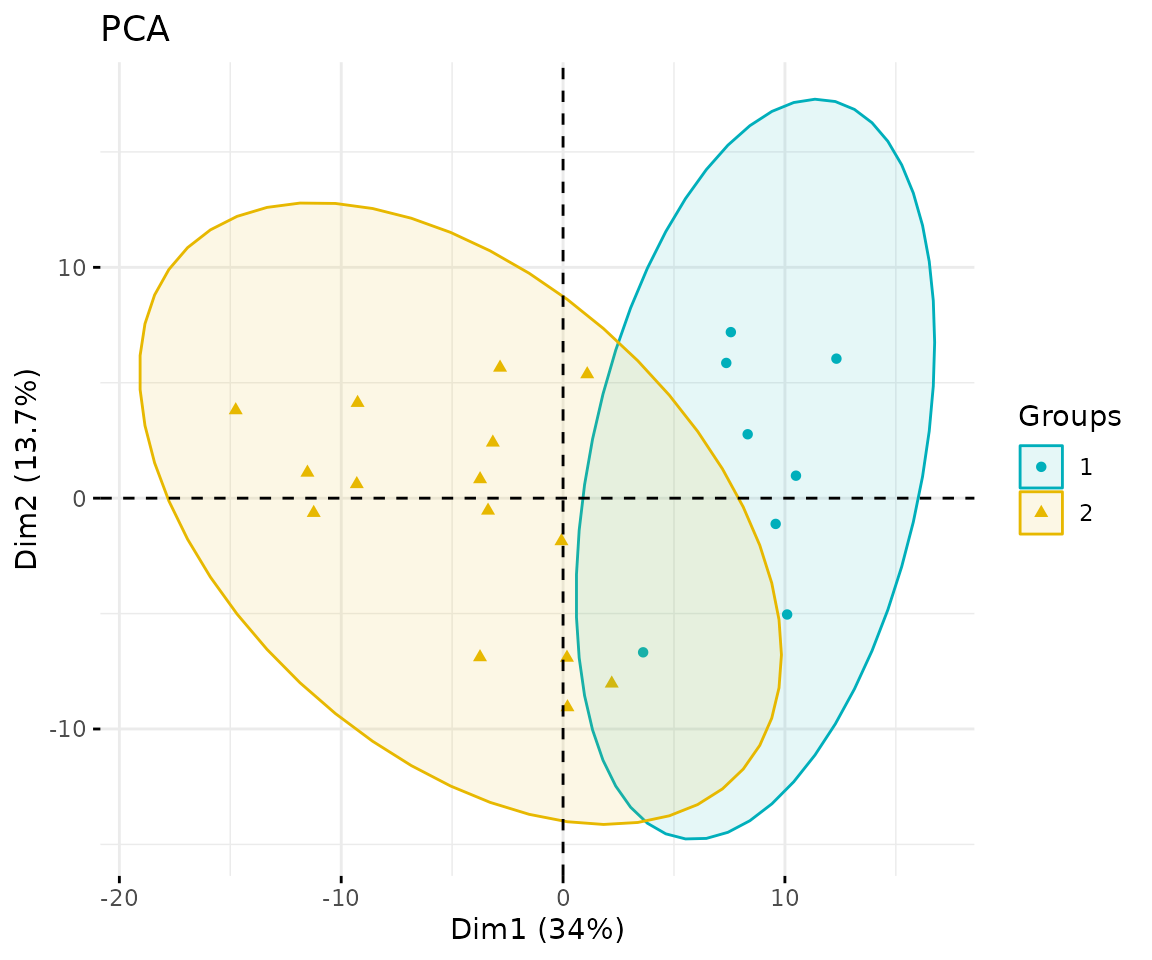
Density plot of abundance distribution The density plot uncovers the distribution of lipid abundance in each sample (line). From this plot, we can have a deeper view of the distribution between samples.
Dimensionality reduction
Dimensionality reduction is commonly used when dealing with large numbers of observations and/or large numbers of variables in lipids analysis. It transforms data from a high-dimensional space into a low-dimensional space so that it retains vital properties of the original data and is close to its intrinsic dimension.
Here we provide 3 dimensionality reduction methods, PCA, t-SNE, UMAP. As for the number of groups shown on the PCA, t-SNE, and UMAP plot, it can be defined by users (default: 2 groups).
PCA
PCA (Principal component analysis) is an unsupervised linear dimensionality reduction and data visualization technique for high dimensional data, which tries to preserve the global structure of the data. Scaling (by default) indicates that the variables should be scaled to have unit variance before the analysis takes place, which removes the bias towards high variances. In general, scaling (standardization) is advisable for data transformation when the variables in the original dataset have been measured on a significantly different scale. As for the centering options (by default), we offer the option of mean-centering, subtracting the mean of each variable from the values, making the mean of each variable equal to zero. It can help users to avoid the interference of misleading information given by the overall mean.
# data processing
processed_se <- data_process(
se, exclude_missing=TRUE, exclude_missing_pct=70,
replace_na_method='min', replace_na_method_ref=0.5,
normalization='Percentage')
# conduct PCA
result_pca <- dr_pca(
processed_se, scaling=TRUE, centering=TRUE, clustering='kmeans',
cluster_num=2, kmedoids_metric=NULL, distfun=NULL, hclustfun=NULL,
eps=NULL, minPts=NULL, feature_contrib_pc=c(1,2), plot_topN=10)
# result summary
summary(result_pca)
#> Length Class Mode
#> pca_rotated_data 25 data.frame list
#> table_pca_contribution 24 data.frame list
#> interactive_pca 8 plotly list
#> interactive_screePlot 8 plotly list
#> interactive_feature_contribution 8 plotly list
#> interactive_variablePlot 8 plotly list
#> static_pca 9 gg list
#> static_screePlot 9 gg list
#> static_feature_contribution 9 gg list
#> static_variablePlot 9 gg listAfter running the above code, you will obtain a list containing interactive plots, static plots, and tables for three types of distribution plots. (Note: Only static plots are displayed here.)
# view result: PCA plot
result_pca$static_pca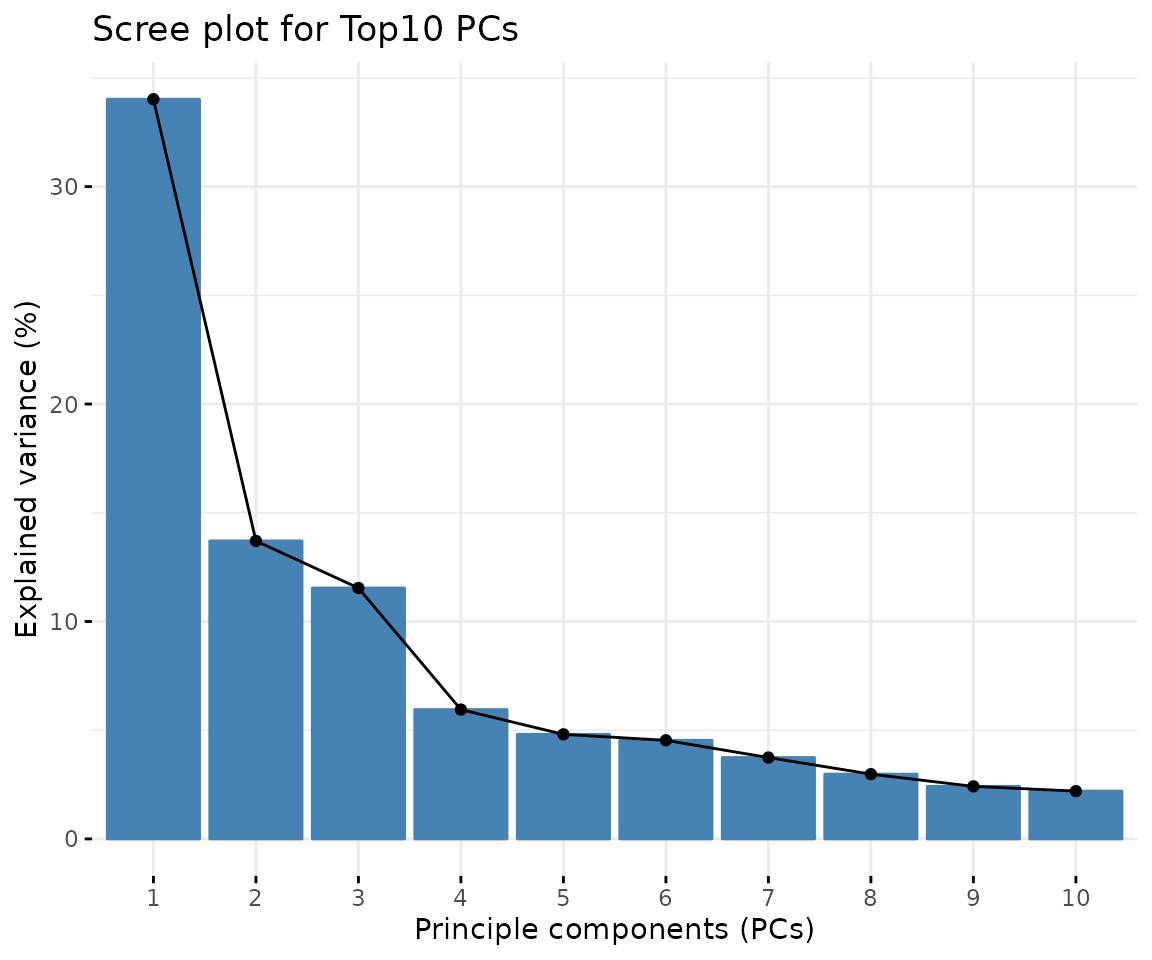
PCA plot
# view result: scree plot of top 10 principle components
result_pca$static_screePlot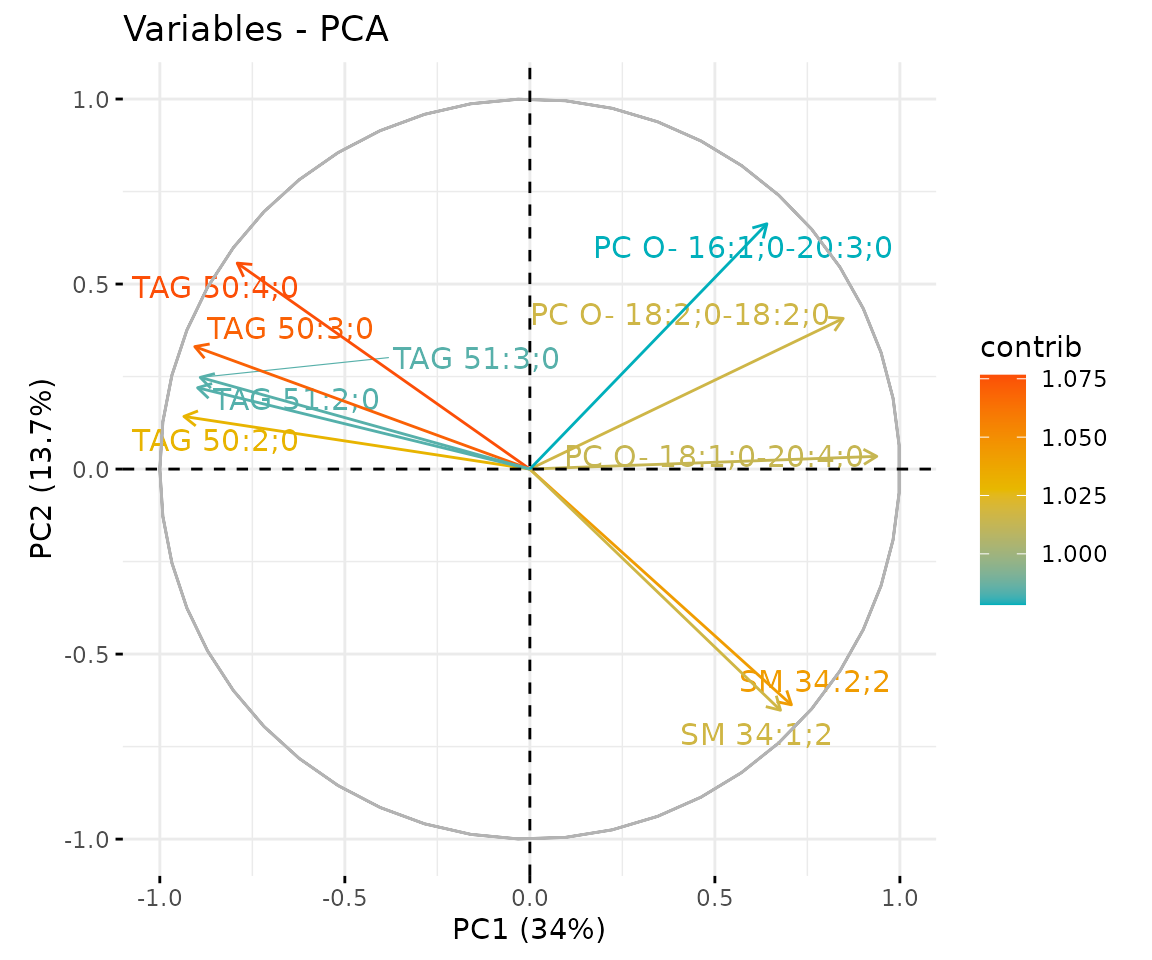
Scree plot A common method for determining the number of PCs to be retained. The ‘elbow’ of the graph indicates all components to the left of this point can explain most variability of the samples
# view result: correlation circle plot of PCA variables
result_pca$static_feature_contribution
Correlation circle plot The correlation circle plot showing the correlation between a feature (lipid species) and a principal component (PC) used as the coordinates of the variable on the PC (Abdi and Williams 2010). The positively correlated variables are in the same quadrants while negatively correlated variables are on the opposite sides of the plot origin. The closer a variable to the edge of the circle, the better it represents on the factor map.
# view result: bar plot of contribution of top 10 features
result_pca$static_variablePlot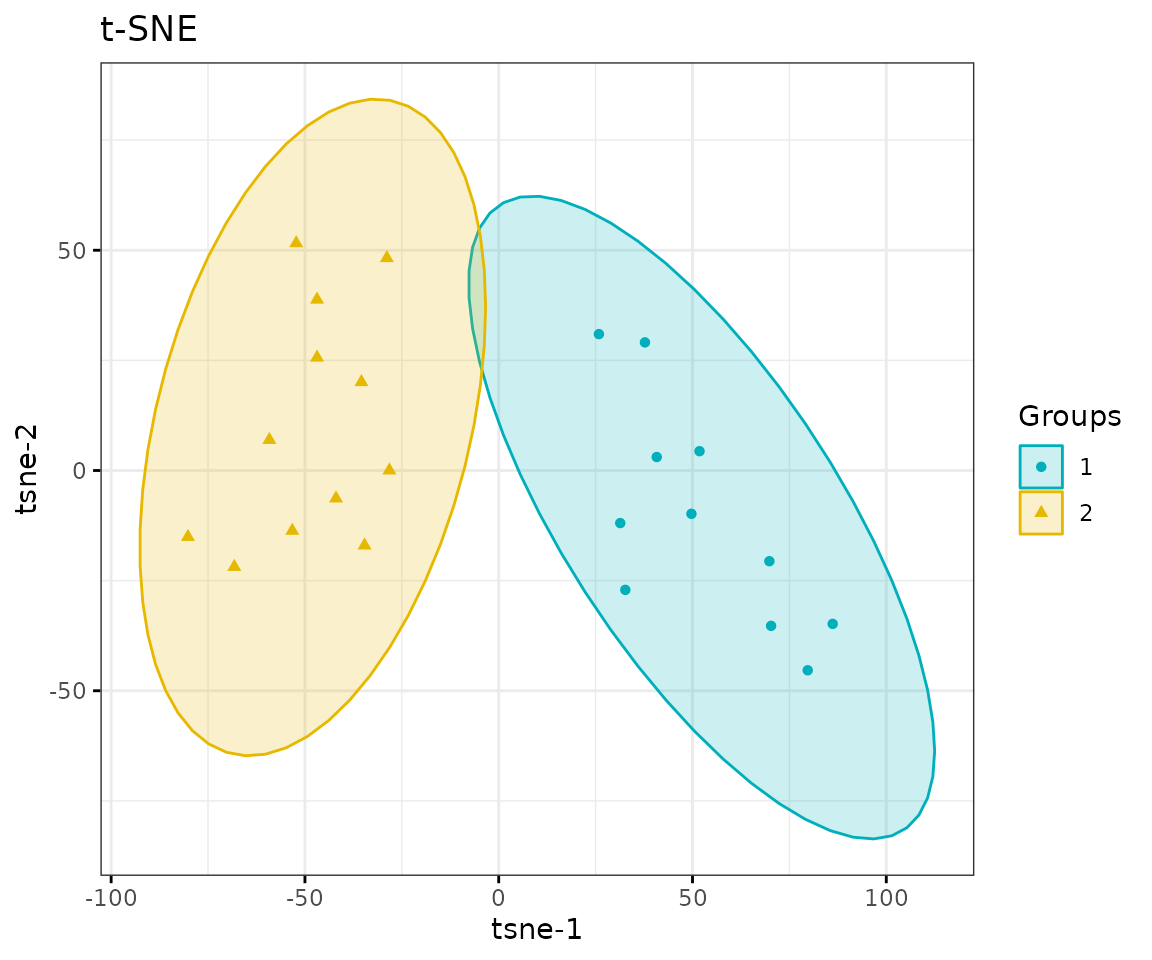
Bar plot of contribution of top 10 features The plot displaysthe features (lipid species) that contribute more to the user-defined principal component.
t-SNE
t-SNE (t-Distributed Stochastic Neighbour Embedding) is an
unsupervised non-linear dimensionality reduction technique that tries to
retain the local structure(cluster) of data when visualising the
high-dimensional datasets. Package Rtsne is used for
calculation, and PCA is applied as a pre-processing step. In t-SNE,
perplexity and max_iter are adjustable for
users. The perplexity may be considered as a knob that sets
the number of effective nearest neighbours, while max_iter
is the maximum number of iterations to perform. The typical perplexity
range between 5 and 50, but if the t-SNE plot shows a ‘ball’ with
uniformly distributed points, you may need to lower your perplexity
(Van der Maaten and Hinton 2008).
# data processing
processed_se <- data_process(
se, exclude_missing=TRUE, exclude_missing_pct=70,
replace_na_method='min', replace_na_method_ref=0.5,
normalization='Percentage')
# conduct t-SNE
result_tsne <- dr_tsne(
processed_se, pca=TRUE, perplexity=5, max_iter=500, clustering='kmeans',
cluster_num=2, kmedoids_metric=NULL, distfun=NULL, hclustfun=NULL,
eps=NULL, minPts=NULL)
#> Performing PCA
#> Read the 23 x 23 data matrix successfully!
#> OpenMP is working. 1 threads.
#> Using no_dims = 2, perplexity = 5.000000, and theta = 0.000000
#> Computing input similarities...
#> Symmetrizing...
#> Done in 0.00 seconds!
#> Learning embedding...
#> Iteration 50: error is 52.909475 (50 iterations in 0.00 seconds)
#> Iteration 100: error is 54.053368 (50 iterations in 0.00 seconds)
#> Iteration 150: error is 54.290057 (50 iterations in 0.00 seconds)
#> Iteration 200: error is 53.592793 (50 iterations in 0.00 seconds)
#> Iteration 250: error is 61.731717 (50 iterations in 0.00 seconds)
#> Iteration 300: error is 1.747214 (50 iterations in 0.00 seconds)
#> Iteration 350: error is 1.283558 (50 iterations in 0.00 seconds)
#> Iteration 400: error is 0.887796 (50 iterations in 0.00 seconds)
#> Iteration 450: error is 0.528751 (50 iterations in 0.00 seconds)
#> Iteration 500: error is 0.415657 (50 iterations in 0.00 seconds)
#> Fitting performed in 0.00 seconds.
# result summary
summary(result_tsne)
#> Length Class Mode
#> tsne_result 4 data.frame list
#> interactive_tsne 8 plotly list
#> static_tsne 9 gg list
# view result: t-SNE plot
result_tsne$static_tsne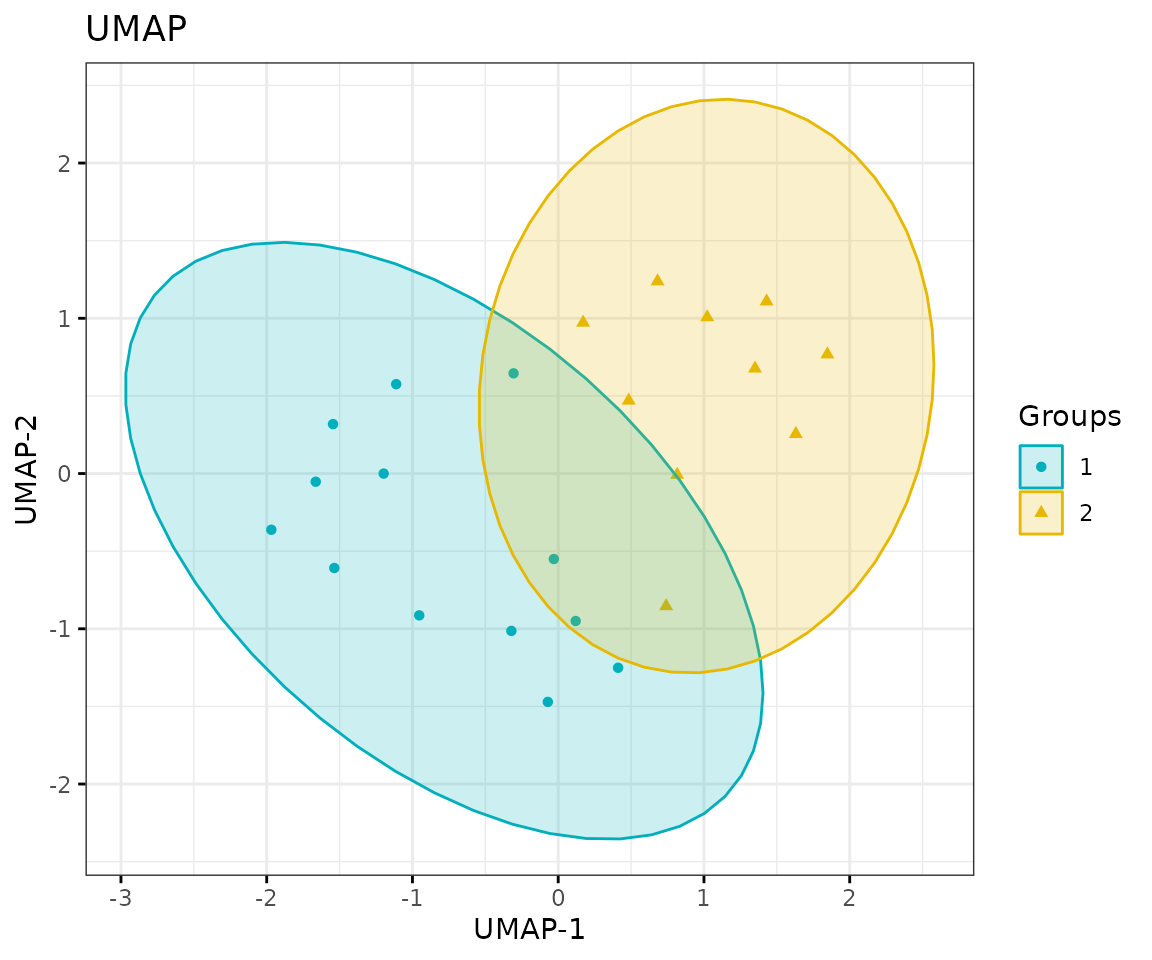
t-SNE plot
UMAP
UMAP (Uniform Manifold Approximation and Projection) using a nonlinear dimensionality reduction method, Manifold learning, which effectively visualizing clusters or groups of data points and their relative proximities. Both tSNE and UMAP are intended to predominantly preserve the local structure that is to group neighbouring data points which certainly delivers a very informative visualization of heterogeneity in the data. The significant difference with t-SNE is scalability, which allows UMAP eliminating the need for applying pre-processing step (such as PCA). Besides, UMAP applies Graph Laplacian for its initialization as tSNE by default implements random initialization. Thus, some people suggest that the key problem of tSNE is the Kullback-Leibler (KL) divergence, which makes UMAP superior over t-SNE. Nevertheless, UMAP’s cluster may not good enough for multi-class pattern classification (McInnes, Healy, and Melville 2018).
The type of distance metric to find nearest neighbors the size of the
local neighborhood (as for the number of neighboring sample points) are
set by parameter metric and n_neighbors.
Larger values lead to more global views of the manifold, while smaller
values result in more local data being preserved. Generally, values are
set in the range of 2 to 100. (default: 15).
# data processing
processed_se <- data_process(
se, exclude_missing=TRUE, exclude_missing_pct=70,
replace_na_method='min', replace_na_method_ref=0.5,
normalization='Percentage')
# conduct UMAP
result_umap <- dr_umap(
processed_se, n_neighbors=15, scaling=TRUE, umap_metric='euclidean',
clustering='kmeans', cluster_num=2, kmedoids_metric=NULL,
distfun=NULL, hclustfun=NULL, eps=NULL, minPts=NULL)
# result summary
summary(result_umap)
#> Length Class Mode
#> umap_result 4 data.frame list
#> interactive_umap 8 plotly list
#> static_umap 9 gg list
# view result: UMAP plot
result_umap$static_umap
UMAP plot
Correlation heatmap
The correlation heatmap illustrates the correlation between samples
or lipid species and also depicts the patterns in each group. The
correlation is calculated by the method defined by parameter
corr_method, and the correlation coefficient is then
clustered depending on method defined by parameter distfun
and the distance defined by parameter hclustfun. Users can
choose to output the sample correlation or lipid correlation results by
the parameter type.
Please note that if the number of lipids or samples is over 50, the names of lipids/samples will not be shown on the heatmap.
Here, we use type='sample' as example.
# data processing
processed_se <- data_process(
se, exclude_missing=TRUE, exclude_missing_pct=70,
replace_na_method='min', replace_na_method_ref=0.5,
normalization='Percentage')
# correlation calculation
result_heatmap <- heatmap_correlation(
processed_se, char=NULL, transform='log10', correlation='pearson',
distfun='maximum', hclustfun='average', type='sample')
# result summary
summary(result_heatmap)
#> Length Class Mode
#> interactive_heatmap 1 IheatmapHorizontal S4
#> static_heatmap 3 recordedplot list
#> corr_coef_matrix 529 -none- numeric
# view result: sample-sample heatmap
result_heatmap$static_heatmap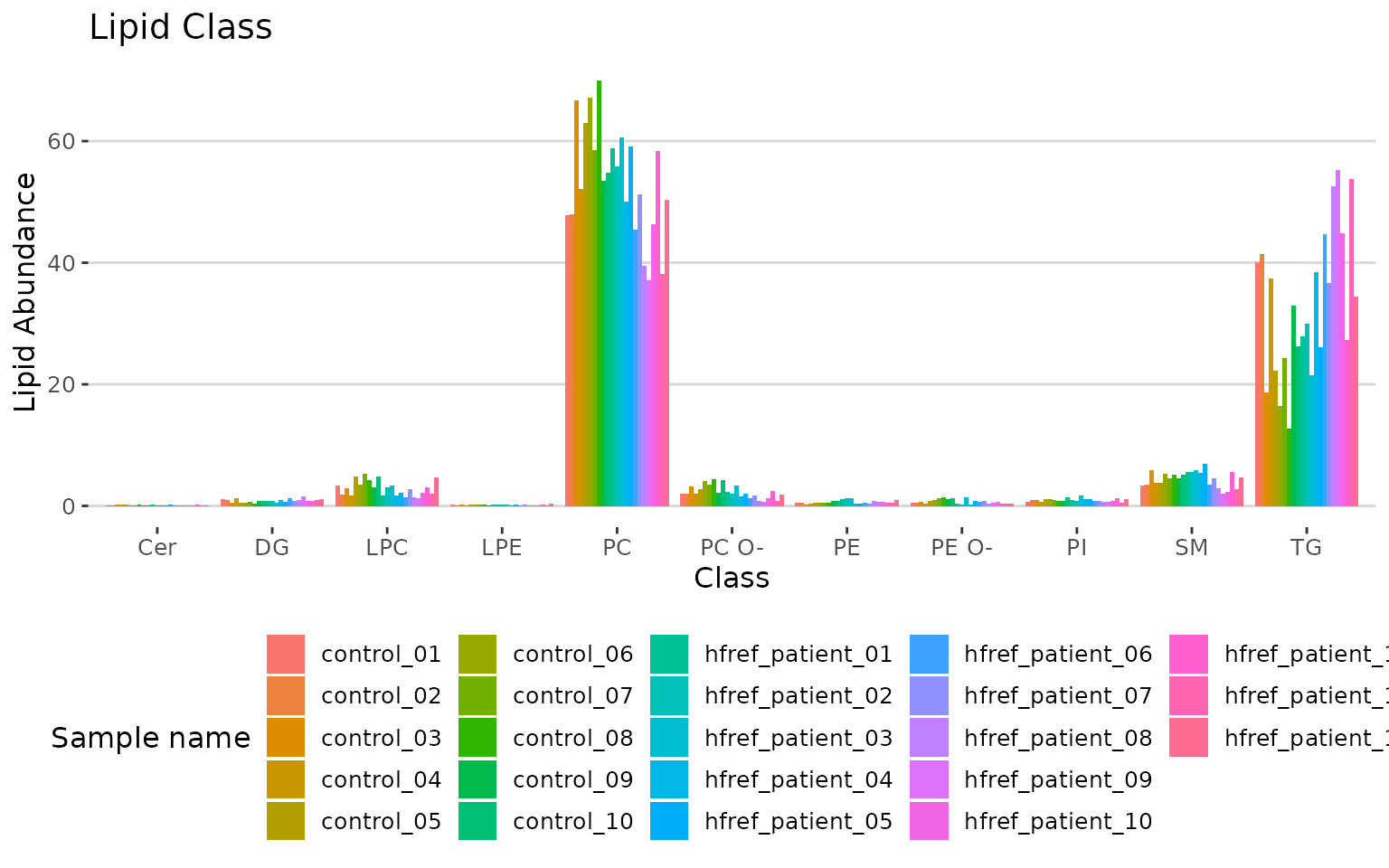
Heatmap of sample to sample correlations Correlations between lipid species are colored from strong positive correlations (red) to no correlation (white).
Lipid characteristics
Now, we are going to take a view of lipid expression over specific lipid characteristics. First, lipids are classified by characteristics selected from the ‘Lipid characteristics’ table. Here, we select “class” as the selected lipid characteristic. The results will be showed by two plots.
# data processing
processed_se <- data_process(
se, exclude_missing=TRUE, exclude_missing_pct=70,
replace_na_method='min', replace_na_method_ref=0.5,
normalization='Percentage')
# list lipid characteristics
list_lipid_char(processed_se)$common_list
#> There are 4 ratio characteristics that can be converted in your dataset.
#> Lipid classification Lipid classification
#> "Category" "Main.Class"
#> Lipid classification Lipid classification
#> "Sub.Class" "class"
#> Fatty acid properties Fatty acid properties
#> "FA" "FA.C"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category1" "FA.Chain.Length.Category2"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category3" "FA.DB"
#> Fatty acid properties Fatty acid properties
#> "FA.OH" "FA.Unsaturation.Category1"
#> Fatty acid properties Fatty acid properties
#> "FA.Unsaturation.Category2" "Total.C"
#> Fatty acid properties Fatty acid properties
#> "Total.DB" "Total.FA"
#> Fatty acid properties Physical or chemical properties
#> "Total.OH" "Bilayer.Thickness"
#> Physical or chemical properties Physical or chemical properties
#> "Bond.type" "Headgroup.Charge"
#> Physical or chemical properties Physical or chemical properties
#> "Intrinsic.Curvature" "Lateral.Diffusion"
#> Physical or chemical properties Cellular component
#> "Transition.Temperature" "Cellular.Component"
#> Function
#> "Function"
# calculate lipid expression of selected characteristic
result_lipid <- lipid_profiling(processed_se, char="class")
#> There are 4 ratio characteristics that can be converted in your dataset.
# result summary
summary(result_lipid)
#> Length Class Mode
#> interactive_char_barPlot 8 plotly list
#> interactive_lipid_composition 8 plotly list
#> static_char_barPlot 9 gg list
#> static_lipid_composition 9 gg list
#> table_char_barPlot 5 tbl_df list
#> table_lipid_composition 5 tbl_df list
# view result: bar plot
result_lipid$static_char_barPlot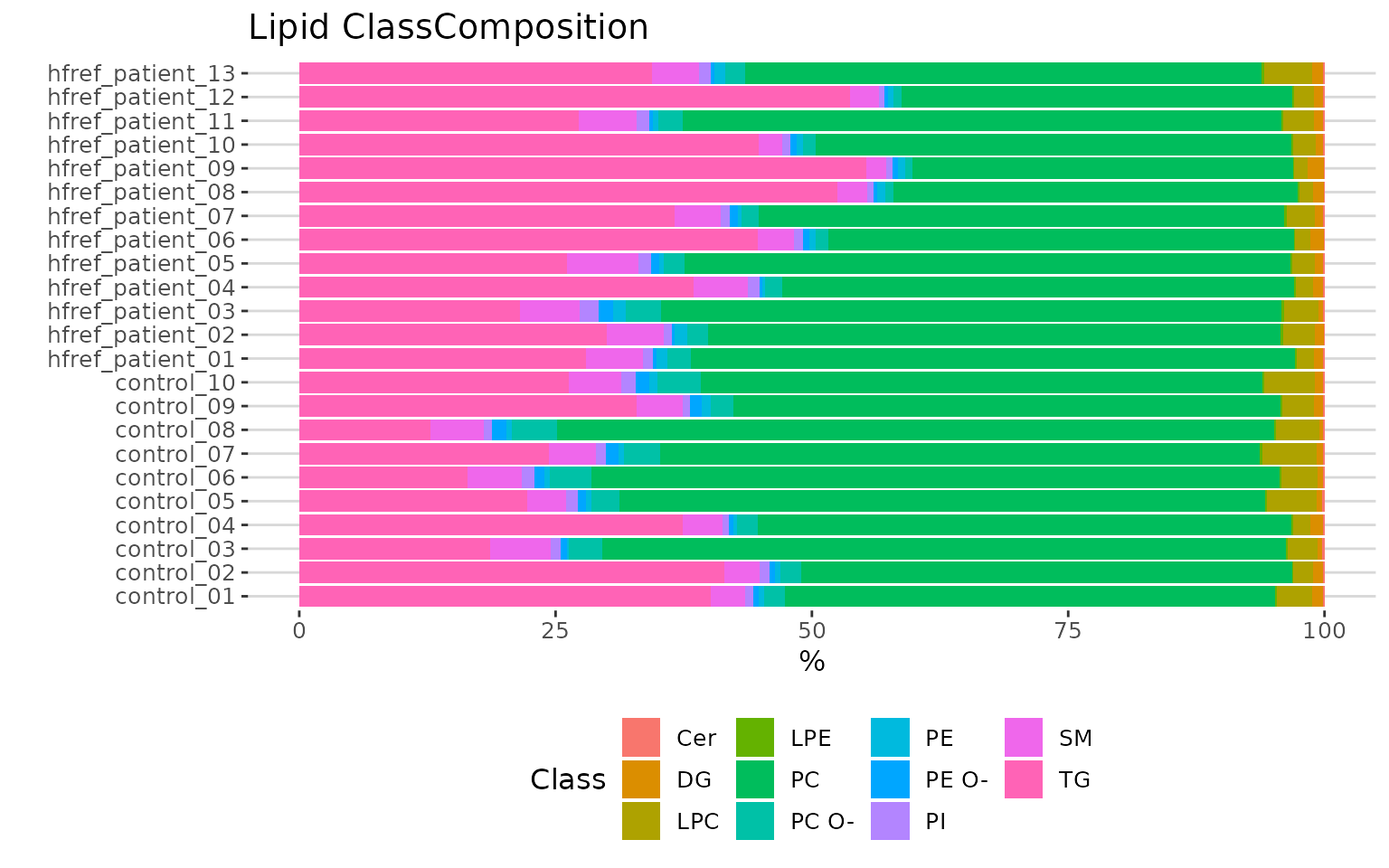
Bar plot classified by selected characteristic The bar plot depicts the abundance level of each sample within each group (e.g., PE, PC) of selected characteristics (e.g., class).
# view result: stacked horizontal bar chart
result_lipid$static_lipid_composition 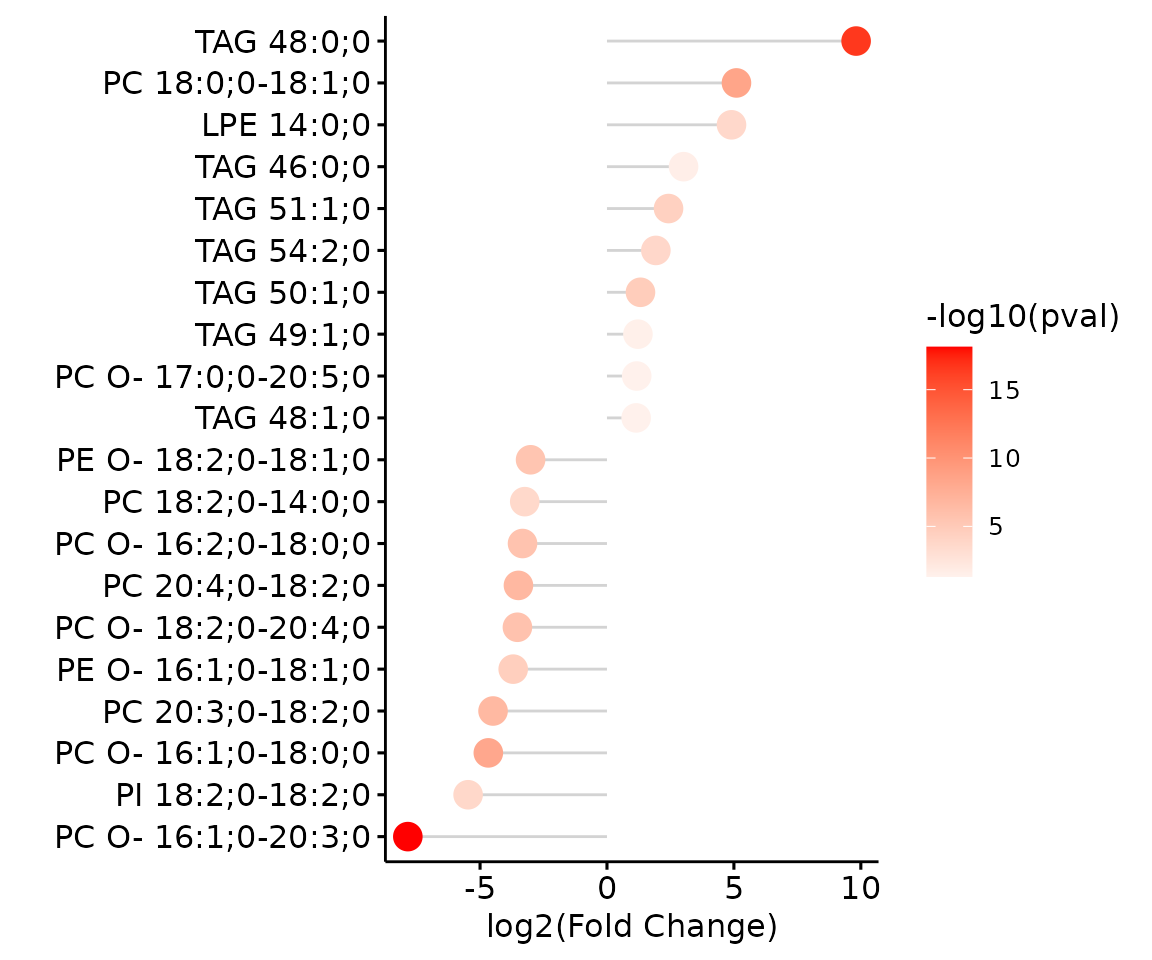
Lipid class composition The stacked horizontal bar chart illustrates the percentage of characteristics in each sample. The variability of percentage between samples can also be obtained from this plot.
Differential expression
After overviewing the lipid data, then we move on to differential expression to identify the significant lipid species and lipid characteristics. Differential Expression is divided into two main analyses, ‘Lipid species analysis’ and ‘Lipid characteristics analysis’. Further analysis and visualization methods can also be conducted based on the results of differential expressed analysis.
-
Lipid species analysis: The lipid species analysis explores the significant lipid species based on differentially expressed analysis. Data are analyzed based on each lipid species. Further analysis and visualization methods, include
- dimensionality reduction,
- hierarchical clustering,
- characteristics association.
-
Lipid characteristics analysis: The lipid characteristics analysis explores the significant lipid characteristics. Lipid species are categorized and summarized into a new lipid abundance table according to a selected lipid characteristic. The abundance of all lipid species of the same categories are summed up, then conduct differential expressed analysis. Further analysis and visualization methods include
- dimensionality reduction,
- hierarchical clustering,
- double bond-chain length analysis.
Lipid species analysis
Now, let’s start with the analysis of lipid species.
Differential expression analysis
For lipid species analysis section, differential expression analysis is performed to figure out significant lipid species. In short, samples will be divided into two groups (independent) according to the input “Group Information” table.
# data processing
processed_se <- data_process(
se, exclude_missing=TRUE, exclude_missing_pct=70,
replace_na_method='min', replace_na_method_ref=0.5,
normalization='Percentage')
# conduct differential expression analysis of lipid species
deSp_se <- deSp_twoGroup(
processed_se, ref_group='ctrl', test='t-test',
significant='pval', p_cutoff=0.05, FC_cutoff=1, transform='log10')After running the above code, a SummarizedExperiment object
deSp_se will be returned containing the analysis results.
This object can be used as input for plotting and further analyses such
as dimensionality reduction, hierarchical clustering, characteristics association, enrichment analysis, and network
analysis.
deSp_se includes the input abundance data, lipid
characteristic table, group information table, analysis results, and
some some setting of input parameters. You can view the data in
deSp_se by
LipidSigR::extract_summarized_experiment.
# view differential expression analysis of lipid species
deSp_result <- extract_summarized_experiment(deSp_se)
# result summary
summary(deSp_result)
#> Length Class Mode
#> abundance 24 data.frame list
#> lipid_char_table 72 data.frame list
#> group_info 5 data.frame list
#> all_deSp_result 15 data.frame list
#> sig_deSp_result 15 data.frame list
#> processed_abundance 24 data.frame list
#> significant 1 -none- character
#> p_cutoff 1 -none- numeric
#> FC_cutoff 1 -none- numeric
#> transform 1 -none- characterThe differential expression analysis result can be input for plotting MA plots, volcano plots, and lollipop plots. (Note: Only static plots are displayed here.)
# plot differential expression analysis result
deSp_plot <- plot_deSp_twoGroup(deSp_se)
# result summary
summary(deSp_plot)
#> Length Class Mode
#> interactive_de_lipid 8 plotly list
#> interactive_maPlot 8 plotly list
#> interactive_volcanoPlot 8 plotly list
#> static_de_lipid 10 gg list
#> static_maPlot 9 gg list
#> static_volcanoPlot 9 gg list
#> table_de_lipid 9 data.frame list
#> table_ma_volcano 9 data.frame list
# view result: lollipop chart
deSp_plot$static_de_lipid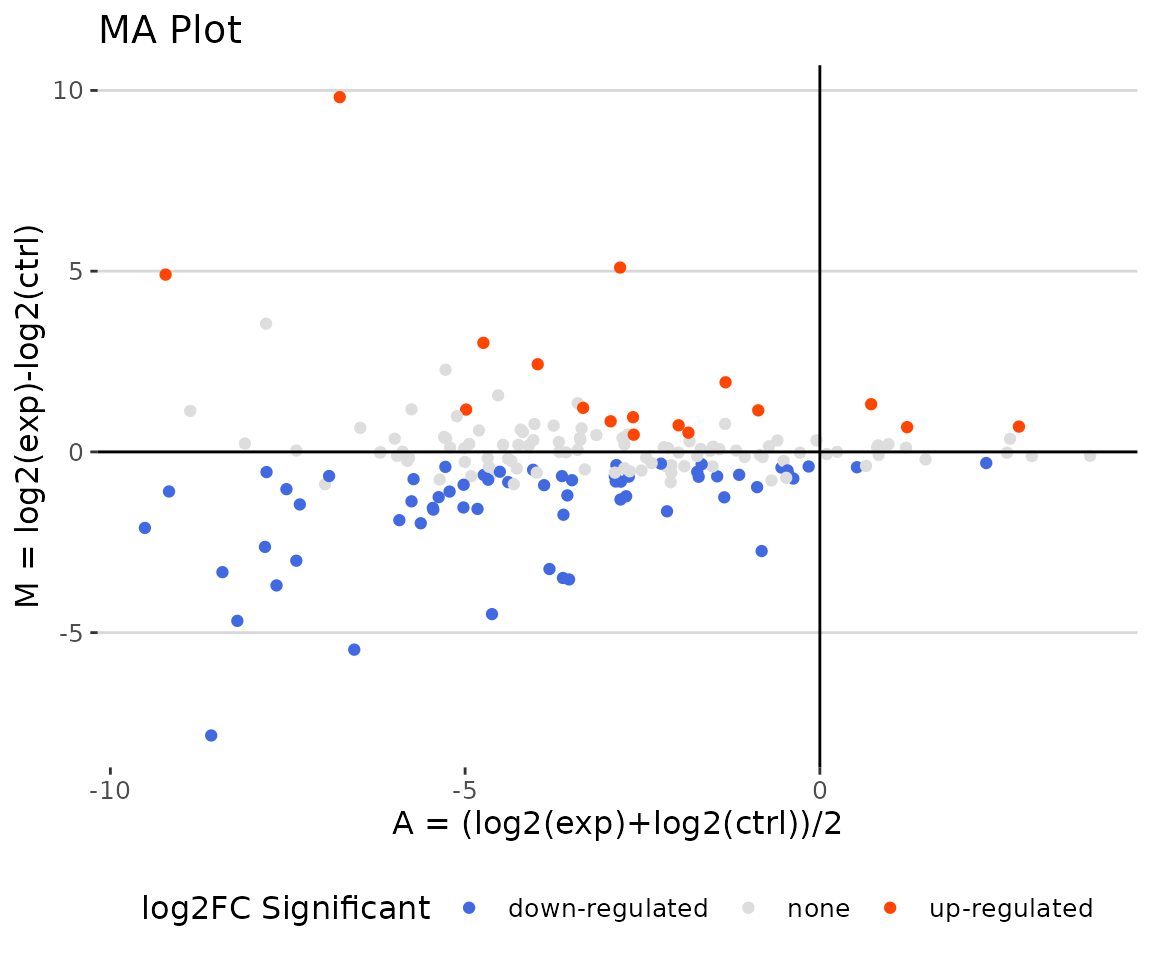
Lollipop chart of lipid species analysis The
lollipop chart reveals the lipid species that pass chosen cut-offs. The
x-axis shows log2 fold change while the y-axis is a list of lipids
species. The color of the point is determined by
-log10(adj_value/p-value).
# view result: MA plot
deSp_plot$static_maPlot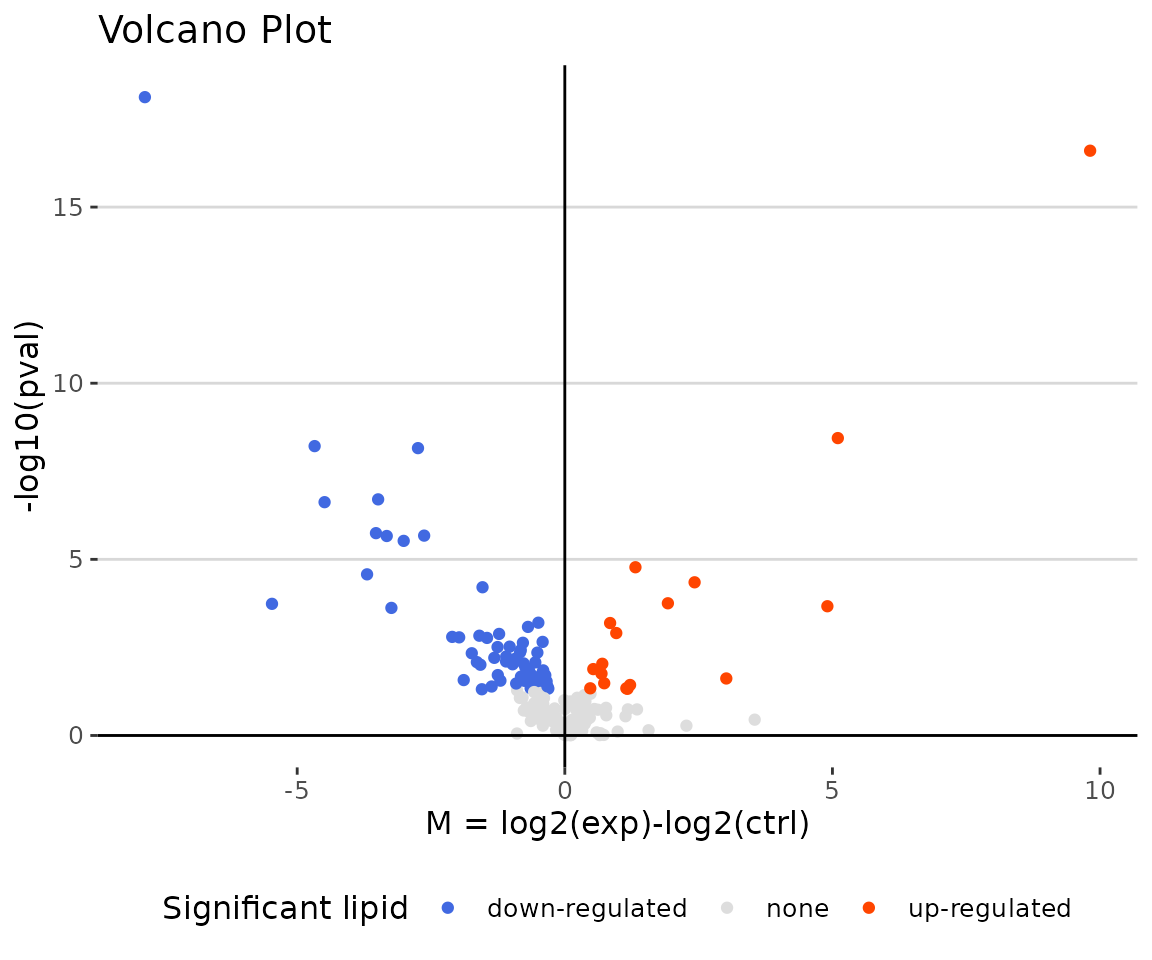
MA plot The MA plot indicates three groups of lipid species, up-regulated(red), down-regulated(blue), and non-significant(grey).
# view result: volcano plot
deSp_plot$static_volcanoPlot 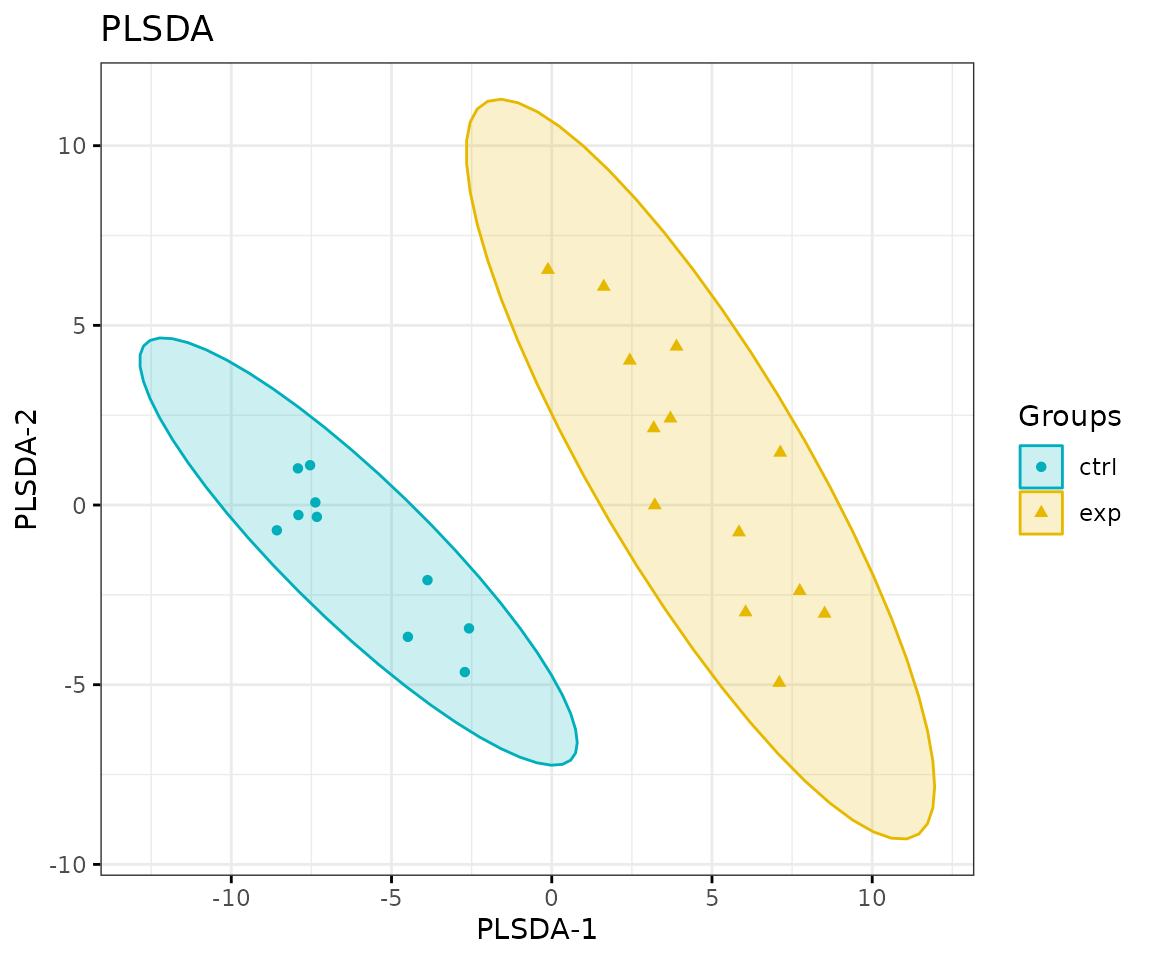
Volcano plot The volcano plot illustrates a similar concept to the MA plot. These points visually identify the most biologically significant lipid species (red for up-regulated, blue for down-regulated, and grey for non-significant).
You can further plot an abundance box plot for any lipid species of
interest by LipidSigR::boxPlot_feature_twoGroup.
For example, let’s use TAG 48:0;0, a significant lipid
species from the lollipop above.
# plot abundance box plot of 'TAG 48:0;0'
boxPlot_result <- boxPlot_feature_twoGroup(
processed_se, feature='TAG 48:0;0', ref_group='ctrl', test='t-test',
transform='log10')
# result summary
summary(boxPlot_result)
#> Length Class Mode
#> static_boxPlot 9 gg list
#> table_boxplot 7 data.frame list
#> table_stat 5 rstatix_test list
# view result: static box plot
boxPlot_result$static_boxPlot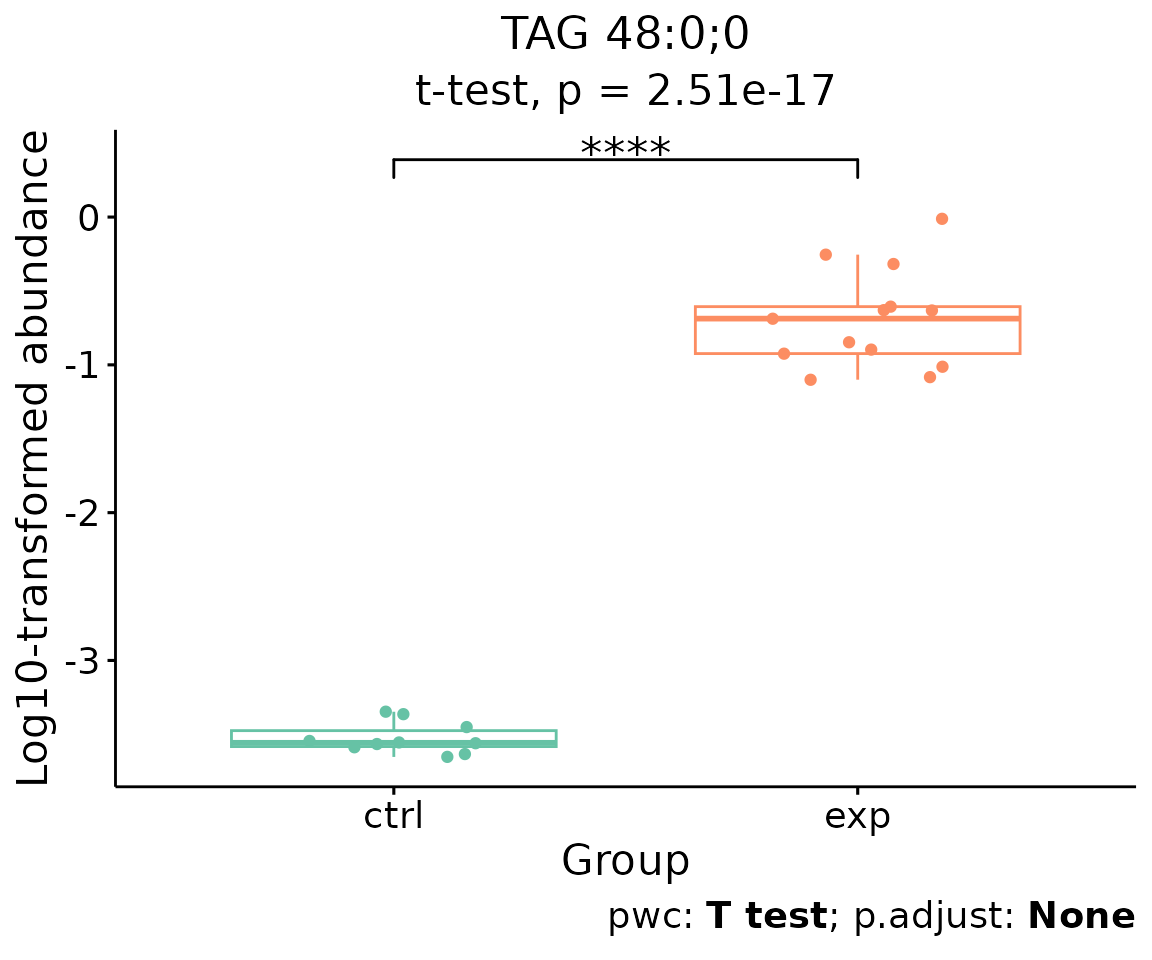
Box plot of lipid abundance An asterisk sign indicates significant differences between groups. The absence of an asterisk or line denotes a non-significant difference between groups.
Dimension reduction
Dimension reduction is common when dealing with large numbers of observations and/or large numbers of variables in lipids analysis. It transforms data from a high-dimensional space into a low-dimensional space to retain vital properties of the original data and close to its intrinsic dimension.
Here, we provide four dimension reduction methods: in addition to the previously introduced PCA, t-SNE, and UMAP (details in Section PCA, t-SNE, UMAP), we include PLS-DA.
- Note: The input data of this section is the output data of
LipidSigR::deSp_twoGroup.
PCA, t-SNE, UMAP
Previous sections introduced details of PCA (Principal Component Analysis), t-SNE (t-distributed stochastic neighbor embedding), and UMAP (Uniform Manifold Approximation and Projection) (please refer to Section PCA, t-SNE, UMAP).
The only difference in running the functions is that the input data
changes from processed_se to deSp_se (output
from lipid species analysis).
Here, we use PCA as an example.
# conduct PCA
result_pca <- dr_pca(
deSp_se, scaling=TRUE, centering=TRUE, clustering='kmeans',
cluster_num=2, kmedoids_metric=NULL, distfun=NULL, hclustfun=NULL,
eps=NULL, minPts=NULL, feature_contrib_pc=c(1,2), plot_topN=10)
# result summary
summary(result_pca)
#> Length Class Mode
#> pca_rotated_data 25 data.frame list
#> table_pca_contribution 24 data.frame list
#> interactive_pca 8 plotly list
#> interactive_screePlot 8 plotly list
#> interactive_feature_contribution 8 plotly list
#> interactive_variablePlot 8 plotly list
#> static_pca 9 gg list
#> static_screePlot 9 gg list
#> static_feature_contribution 9 gg list
#> static_variablePlot 9 gg listPLS-DA
The input data is the output data of deSp_twoGroup from
lipid species analysis.
# conduct PLSDA
result_plsda <- dr_plsda(
deSp_se, ncomp=2, scaling=TRUE, clustering='group_info', cluster_num=2,
kmedoids_metric=NULL, distfun=NULL, hclustfun=NULL, eps=NULL, minPts=NULL)
# result summary
summary(result_plsda)
#> Length Class Mode
#> plsda_result 4 data.frame list
#> table_plsda_loading 2 data.frame list
#> interacitve_plsda 8 plotly list
#> interactive_loadingPlot 8 plotly list
#> static_plsda 9 gg list
#> static_loadingPlot 9 gg list
# view result: PLS-DA plot
result_plsda$static_plsda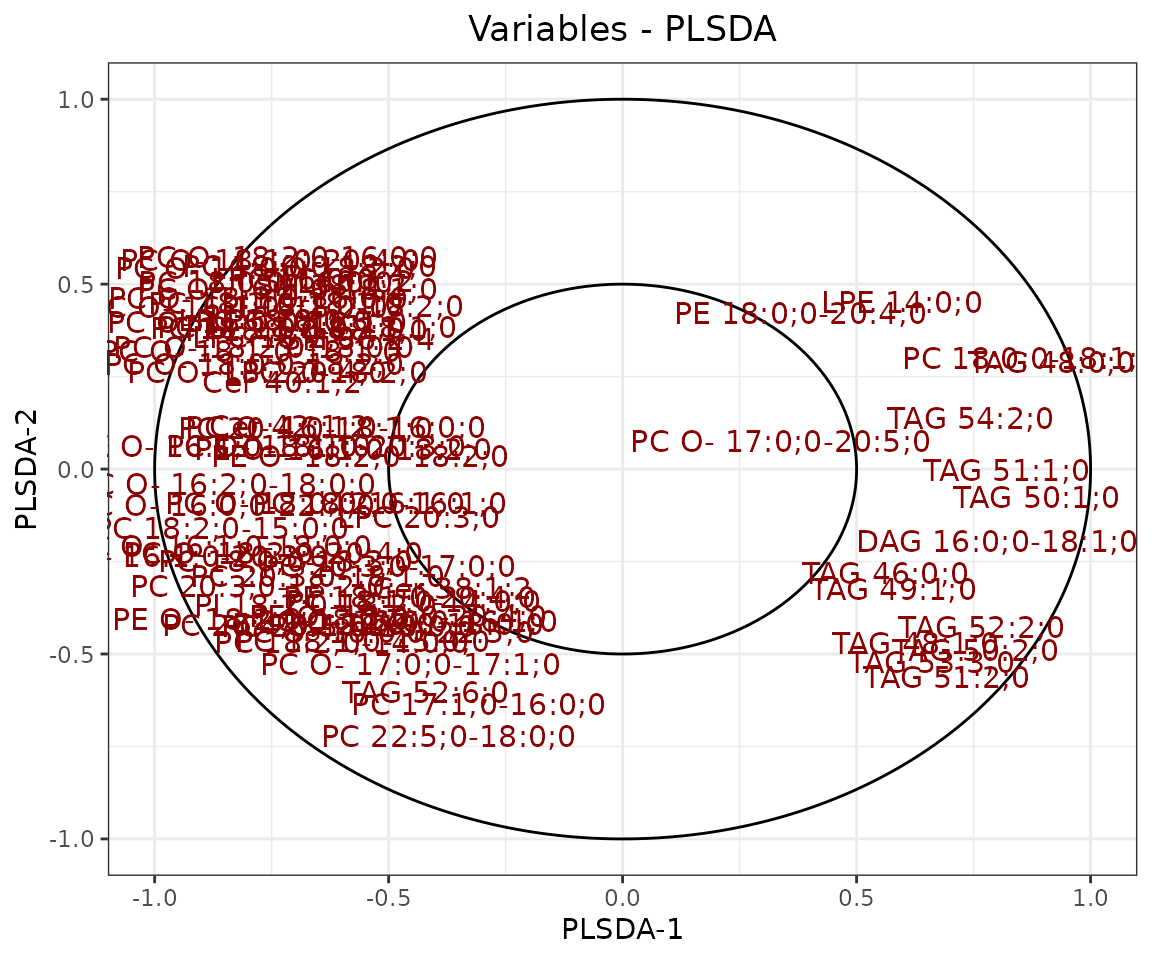
PLS-DA plot
# view result: PLS-DA loading plot
result_plsda$static_loadingPlot 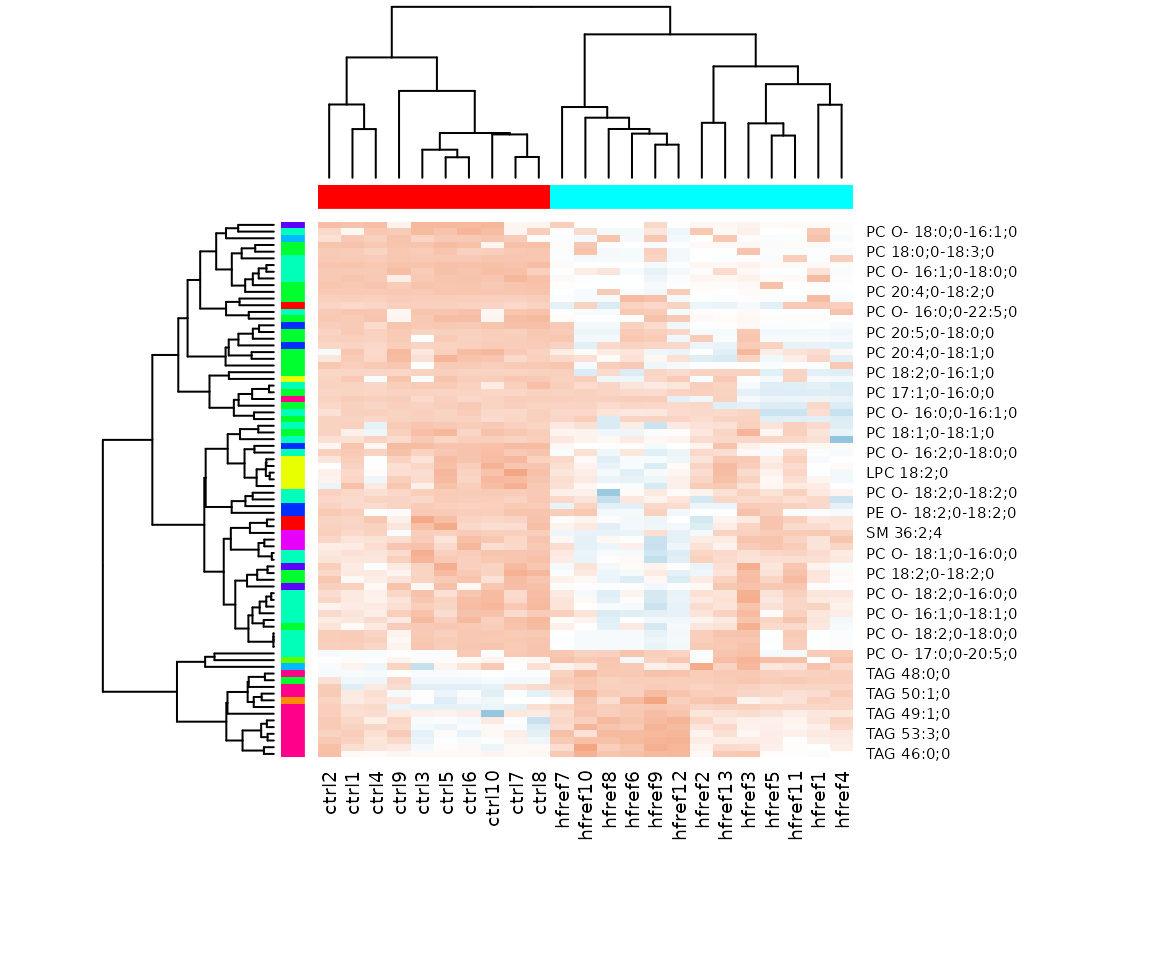
Loading plot In the PLS-DA loading plot, the distance to the center of the variables indicates the contribution of the variable. The value of the x-axis reveals the contribution of the variable to PLS-DA-1, whereas the value of the y-axis discloses the contribution of the variable to PLS-DA-2.
Hierarchical clustering
Based on the results of differential expression analysis, we further
take a look at differences of lipid species between the control group
and the experimental group. Lipid species derived from two groups are
clustered and visualized on heatmap by hierarchical clustering. Users
can choose to output the results of all lipid species or only
significant lipid species by the parameter type.
The top of the heatmap is grouped by sample group (top annotation)
while the side of the heatmap (row annotation) can be chosen from
lipid_char_table, such as class, structural category,
functional category, total length, total double bond (Total.DB),
hydroxyl group number (Total.OH), the double bond of fatty acid(FA.DB),
hydroxyl group number of fatty acid(FA.OH).
# list available lipid characteristics
list_lipid_char(processed_se)$common_list
#> There are 4 ratio characteristics that can be converted in your dataset.
#> Lipid classification Lipid classification
#> "Category" "Main.Class"
#> Lipid classification Lipid classification
#> "Sub.Class" "class"
#> Fatty acid properties Fatty acid properties
#> "FA" "FA.C"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category1" "FA.Chain.Length.Category2"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category3" "FA.DB"
#> Fatty acid properties Fatty acid properties
#> "FA.OH" "FA.Unsaturation.Category1"
#> Fatty acid properties Fatty acid properties
#> "FA.Unsaturation.Category2" "Total.C"
#> Fatty acid properties Fatty acid properties
#> "Total.DB" "Total.FA"
#> Fatty acid properties Physical or chemical properties
#> "Total.OH" "Bilayer.Thickness"
#> Physical or chemical properties Physical or chemical properties
#> "Bond.type" "Headgroup.Charge"
#> Physical or chemical properties Physical or chemical properties
#> "Intrinsic.Curvature" "Lateral.Diffusion"
#> Physical or chemical properties Cellular component
#> "Transition.Temperature" "Cellular.Component"
#> Function
#> "Function"
# conduct hierarchical clustering
result_hcluster <- heatmap_clustering(
de_se=deSp_se, char='class', distfun='pearson',
hclustfun='complete', type='sig')
# result summary
summary(result_hcluster)
#> Length Class Mode
#> interactive_heatmap 1 IheatmapHorizontal S4
#> static_heatmap 3 recordedplot list
#> corr_coef_matrix 1840 -none- numeric
# view result: heatmap of significant lipid species
result_hcluster$static_heatmap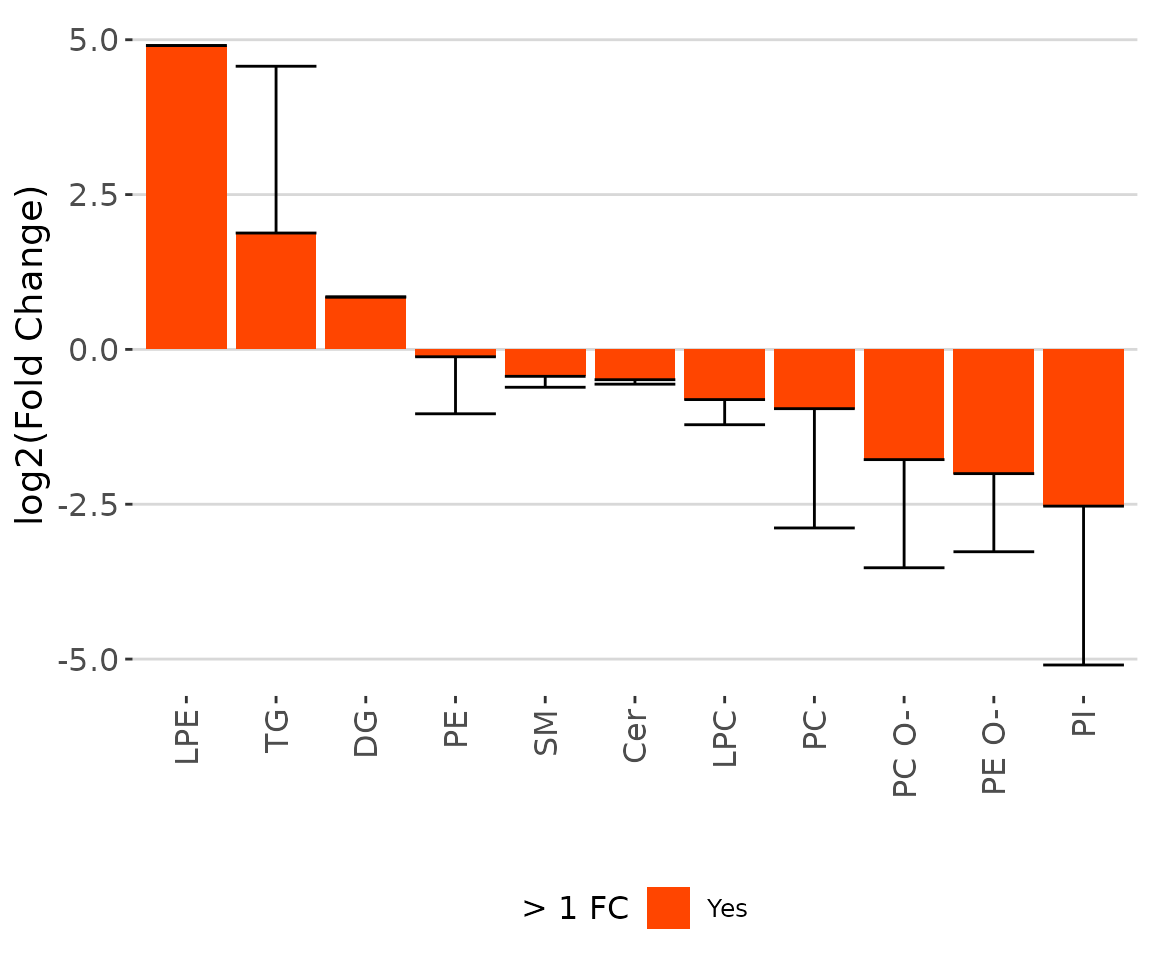
Heatmap of significant lipid species The difference between the two groups by observing the distribution of lipid species.
Characteristics analysis
The characteristics analysis visualizes the difference between
control and experimental groups of significant lipid species categorized
based on different lipid characteristics from
lipid_char_table, such as class, structural category,
functional category, total length, total double bond (Total.DB),
hydroxyl group number (Total.OH), the double bond of fatty acid(FA.DB),
hydroxyl group number of fatty acid(FA.OH).
# list available lipid characteristics
list_lipid_char(processed_se)$common_list
#> There are 4 ratio characteristics that can be converted in your dataset.
#> Lipid classification Lipid classification
#> "Category" "Main.Class"
#> Lipid classification Lipid classification
#> "Sub.Class" "class"
#> Fatty acid properties Fatty acid properties
#> "FA" "FA.C"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category1" "FA.Chain.Length.Category2"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category3" "FA.DB"
#> Fatty acid properties Fatty acid properties
#> "FA.OH" "FA.Unsaturation.Category1"
#> Fatty acid properties Fatty acid properties
#> "FA.Unsaturation.Category2" "Total.C"
#> Fatty acid properties Fatty acid properties
#> "Total.DB" "Total.FA"
#> Fatty acid properties Physical or chemical properties
#> "Total.OH" "Bilayer.Thickness"
#> Physical or chemical properties Physical or chemical properties
#> "Bond.type" "Headgroup.Charge"
#> Physical or chemical properties Physical or chemical properties
#> "Intrinsic.Curvature" "Lateral.Diffusion"
#> Physical or chemical properties Cellular component
#> "Transition.Temperature" "Cellular.Component"
#> Function
#> "Function"
# conduct characteristic analysis
result_char <- char_association(deSp_se, char='class')
# result summary
summary(result_char)
#> Length Class Mode
#> interactive_barPlot 8 plotly list
#> interacitve_lollipop 8 plotly list
#> interactive_wordCloud 8 hwordcloud list
#> static_barPlot 9 gg list
#> static_lollipop 9 gg list
#> static_wordCloud 3 recordedplot list
#> table_barPlot 7 tbl_df list
#> table_lollipop 10 tbl_df list
#> table_wordCloud 2 tbl_df list
# view result: bar chart
result_char$static_barPlot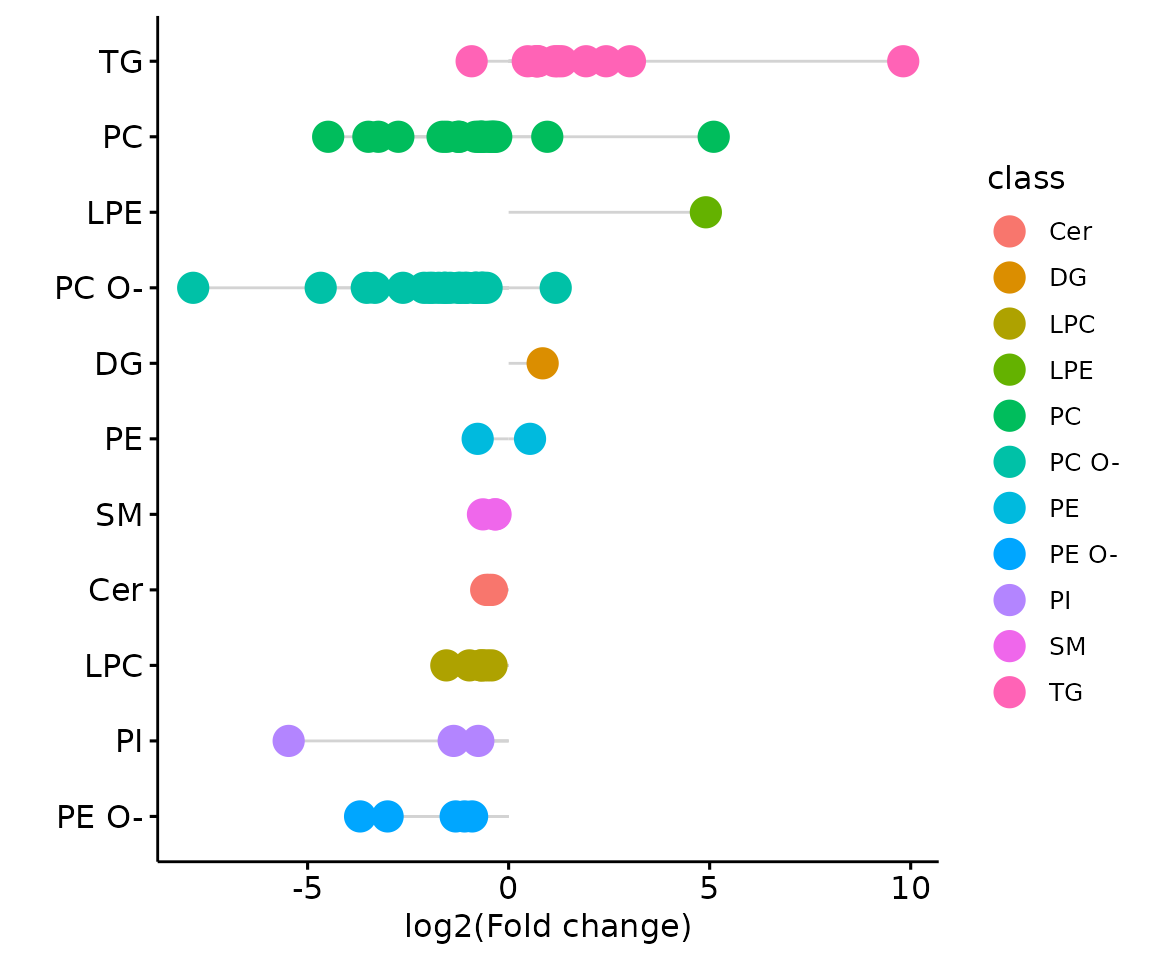
The bar chart of significant groups The bar chart shows the significant groups (values) with mean fold change over 2 in the selected characteristics by colors (red for significant and black for insignificant).
# view result: lollipop plot
result_char$static_lollipop
The lollipop chart of all significant groups The lollipop chart compares multiple values simultaneously and it aligns the log2(fold change) of all significant groups (values) within the selected characteristics.
# view result: word cloud
result_char$static_wordCloud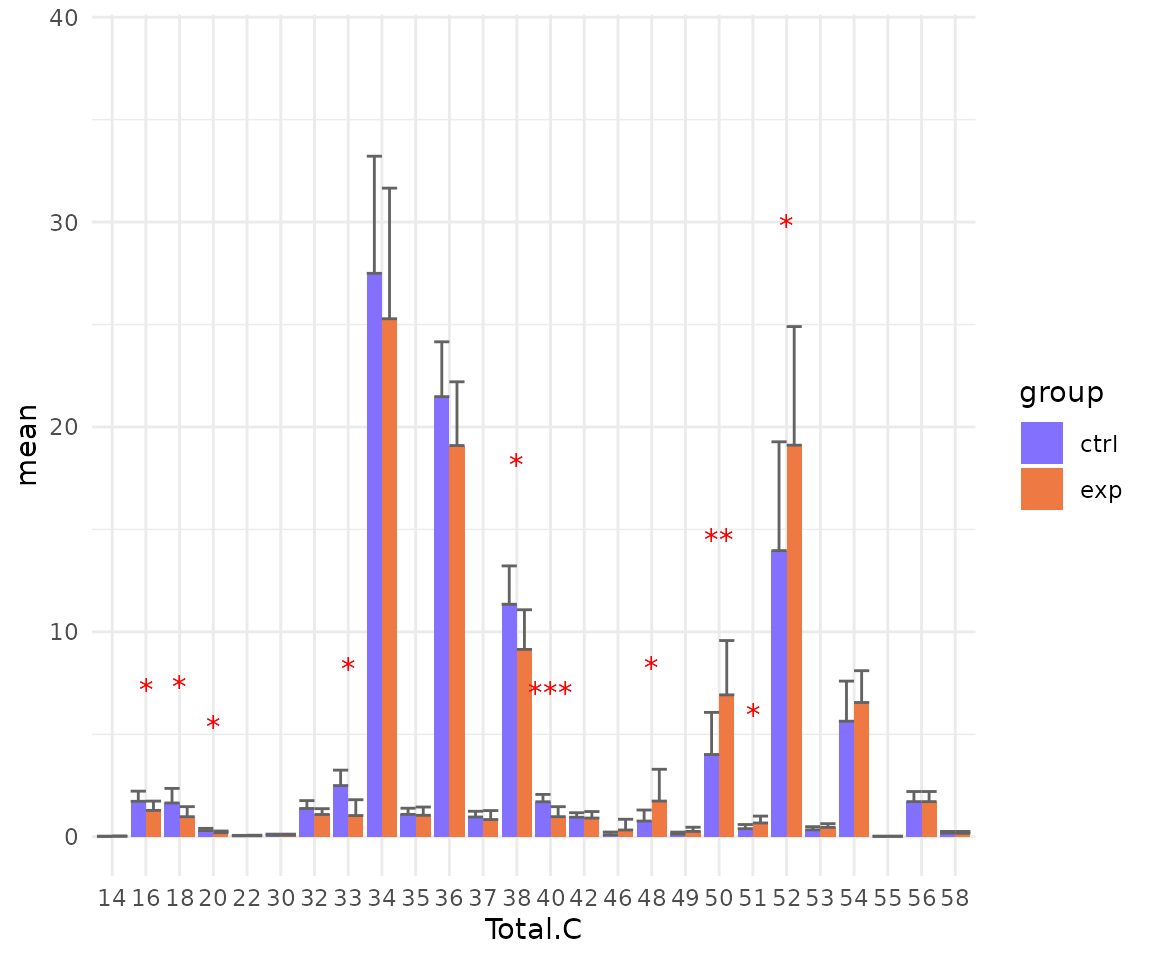
Word cloud with the count of each group The word cloud shows the count of each group(value) of the selected characteristics.
Lipid characteristics analysis
After lipid species analysis, now let’s move on to another main analysis of the Differential expression section – ‘Lipid Characteristics Analysis’. The massive degree of structural diversity of lipids contributes to the functional variety of lipids. The characteristics can range from subtle variance (i.e. the number of a double bond in the fatty acid) to major change (i.e. diverse backbones). In this section, lipid species are categorized and summarized into a new lipid abundance table according to two selected lipid characteristics, then conducted differential expressed analysis. Samples are divided into two groups based on the input ‘Group Information’ table.
Differentially expressed analysis
In differentially expressed analysis, we are going to conduct two procedures of analysis - first is ‘Characteristics’ and then ‘Subgroup of characteristics’.
‘Characteristics’ is based on the first selected
‘characteristics’ while ‘Subgroup of characteristics’
is the subgroup analysis of the previous section. Analyses will be
performed based on parameter char and subChar
selected by users.
Before we begin, let’s calculate the two-way ANOVA and review the results for all lipid characteristics.
# data processing
processed_se <- data_process(
se, exclude_missing=TRUE, exclude_missing_pct=70,
replace_na_method='min', replace_na_method_ref=0.5,
normalization='Percentage')
# two way anova
twoWayAnova_table <- char_2wayAnova(
processed_se, ratio_transform='log2', char_transform='log10')
#> There are 4 ratio characteristics that can be converted in your dataset.
# view result table
head(twoWayAnova_table[, 1:4], 5)
#> aspect characteristic fval_2factors pval_2factors
#> 1 Lipid classification class 5.045694 1.208279e-06
#> 2 Lipid classification Category 5.379765 6.965556e-03
#> 3 Lipid classification Main.Class 3.657973 1.058632e-03
#> 4 Lipid classification Sub.Class 4.993823 4.243797e-06
#> 5 Fatty acid properties Total.FA 7.155695 7.104938e-72From the table returned by LipidSigR::char_2wayAnova, we
have to selected the lipid characteristics of interest as
char and subChar for
LipidSigR::deChar_twoGroup and
LipidSigR::subChar_twoGroup.
Here, we use Total.C as an example.
# data processing
processed_se <- data_process(
se, exclude_missing=TRUE, exclude_missing_pct=70,
replace_na_method='min', replace_na_method_ref=0.5,
normalization='Percentage')
# conduct differential expression of lipid characteristics
deChar_se <- deChar_twoGroup(
processed_se, char="Total.C", ref_group="ctrl", test='t-test',
significant="pval", p_cutoff=0.05, FC_cutoff=1, transform='log10')
#> There are 4 ratio characteristics that can be converted in your dataset.After running the above code, a SummarizedExperiment object
deChar_se will be returned containing the analysis results.
This object can be used as input for plotting and further analyses such
as dimension reduction, and hierarchical clustering.
deChar_se includes the input abundance data, lipid
characteristic table, group information table, analysis results, and
some some setting of input parameters. You can view the data in
deChar_se by
LipidSigR::extract_summarized_experiment.
# view differential expression of lipid characteristics
deChar_result <- extract_summarized_experiment(deChar_se)
# result summary
summary(deChar_result)
#> Length Class Mode
#> abundance 24 data.frame list
#> lipid_char_table 2 data.frame list
#> group_info 5 data.frame list
#> all_deChar_result 23 grouped_df list
#> sig_deChar_result 23 grouped_df list
#> processed_abundance 24 data.frame list
#> char 1 -none- character
#> significant 1 -none- character
#> p_cutoff 1 -none- numeric
#> FC_cutoff 1 -none- numericThe differential expression analysis result can be input for plotting result plots. (Note: Only static plots are displayed here.)
# plot differential expression analysis results
deChar_plot <- plot_deChar_twoGroup(deChar_se)
# result summary
summary(deChar_plot)
#> Length Class Mode
#> static_barPlot 9 gg list
#> static_barPlot_sqrt 9 gg list
#> static_linePlot 9 gg list
#> static_linePlot_sqrt 9 gg list
#> static_boxPlot 10 gg list
#> interactive_barPlot 8 plotly list
#> interactive_barPlot_sqrt 8 plotly list
#> interactive_linePlot 8 plotly list
#> interactive_linePlot_sqrt 8 plotly list
#> interactive_boxPlot 8 plotly list
#> table_barPlot 11 tbl_df list
#> table_linePlot 11 tbl_df list
#> table_boxPlot 7 data.frame list
#> table_char_index 24 data.frame list
#> table_index_stat 13 grouped_df listThe results of ‘Characteristics’ analysis in the first section
# view result: bar plot of selected `char`
deChar_plot$static_barPlot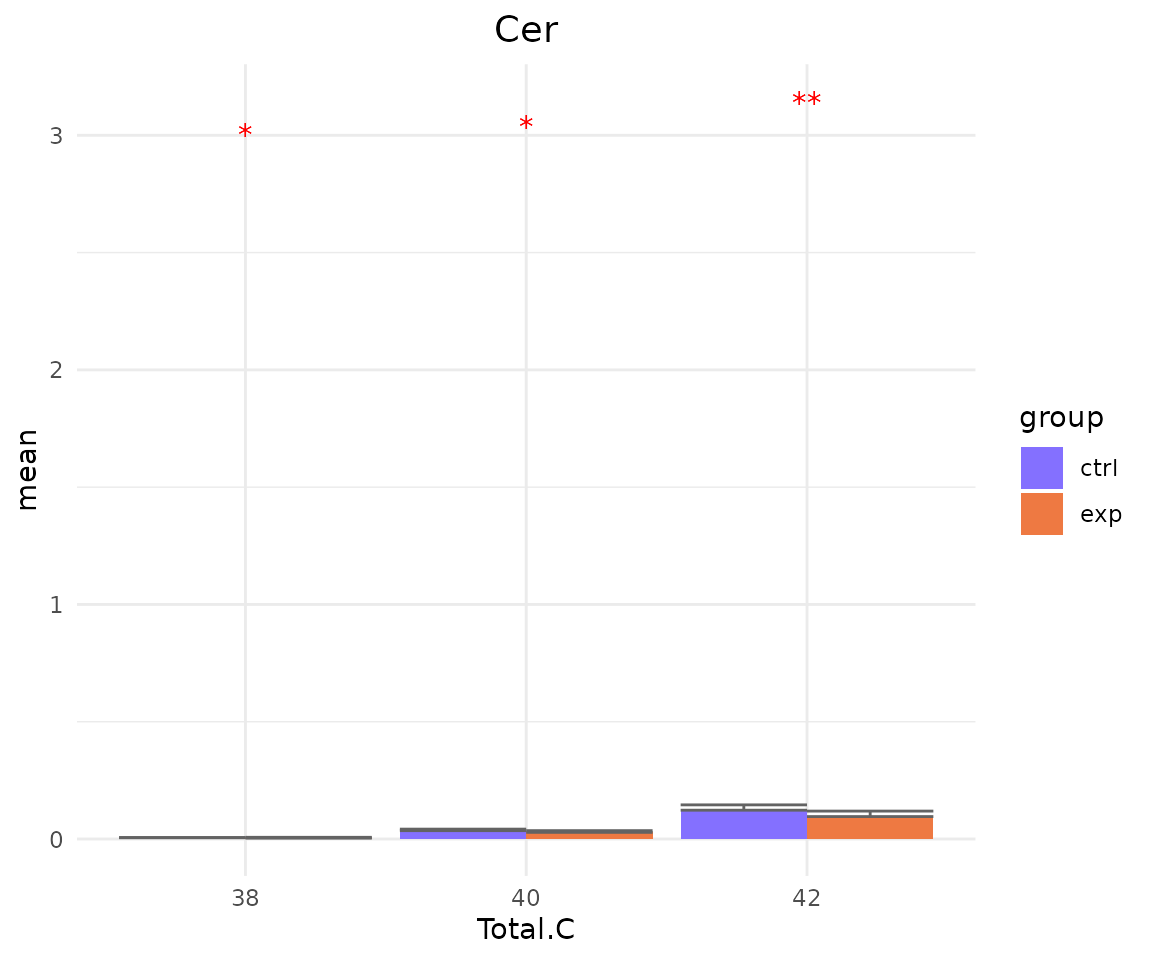
# view result: sqrt-scaled bar plot of selected `char`
deChar_plot$static_barPlot_sqrt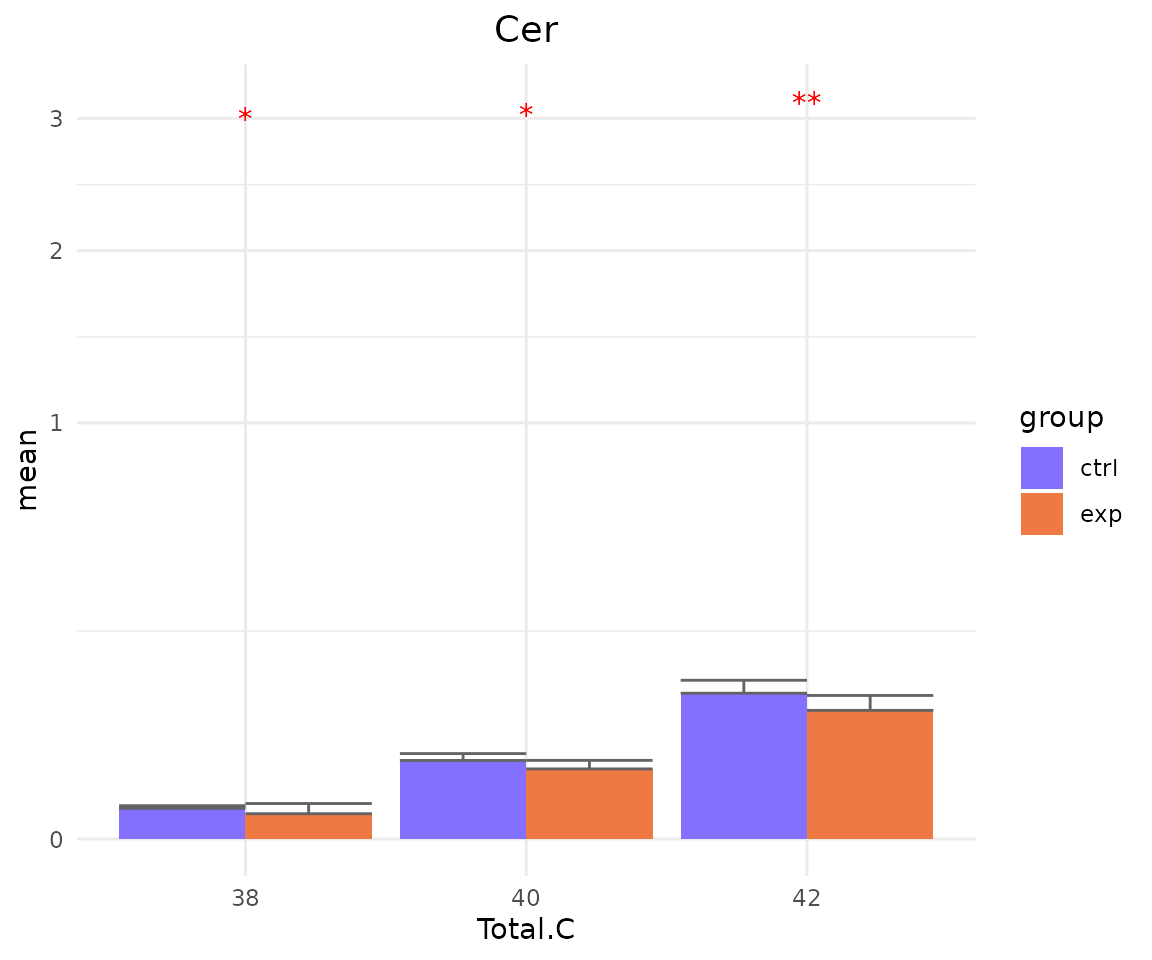
# view result: line plot of `selected char`
deChar_plot$static_linePlot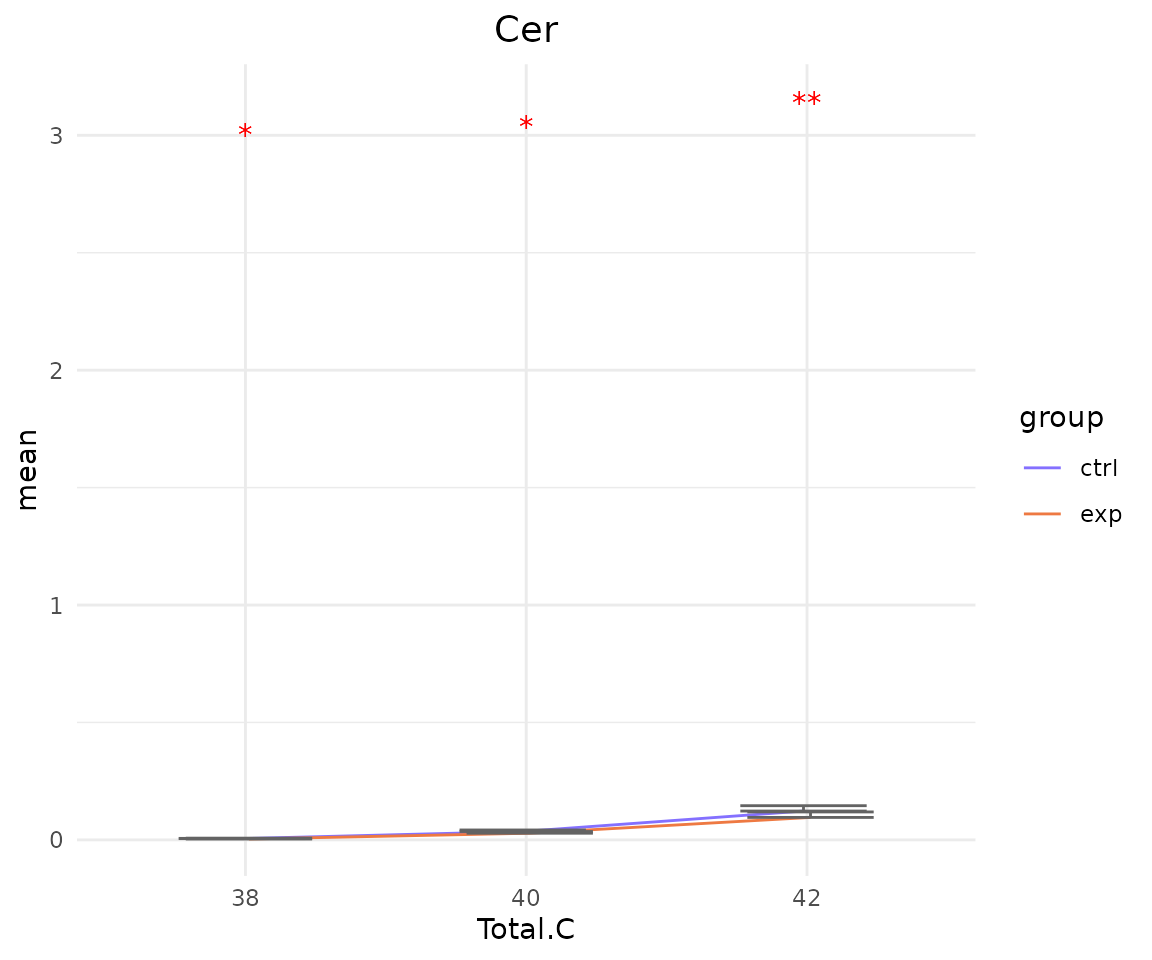
# view result: sqrt-scaled line plot of selected `char`
deChar_plot$static_linePlot_sqrt 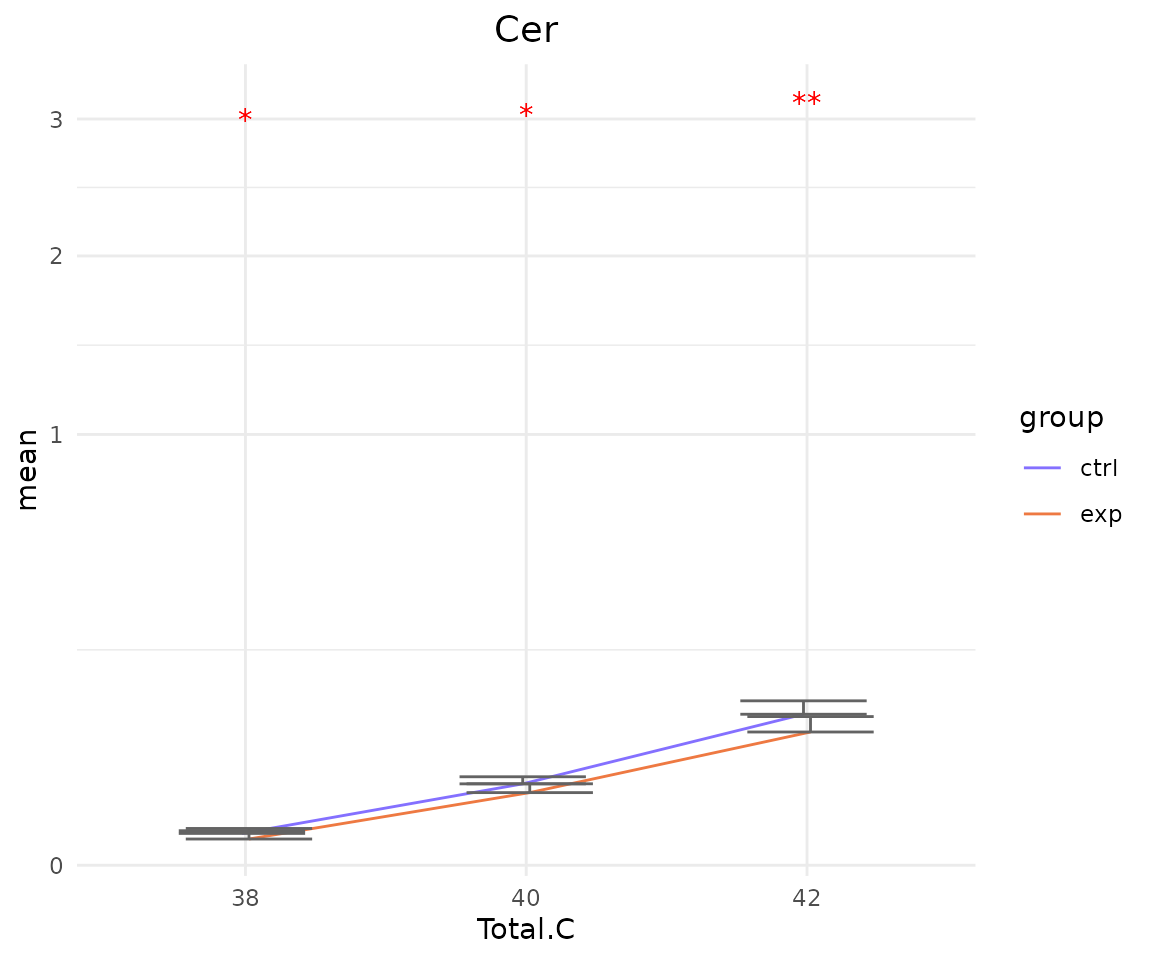
# view result: box plot of selected `char`
deChar_plot$static_boxPlot 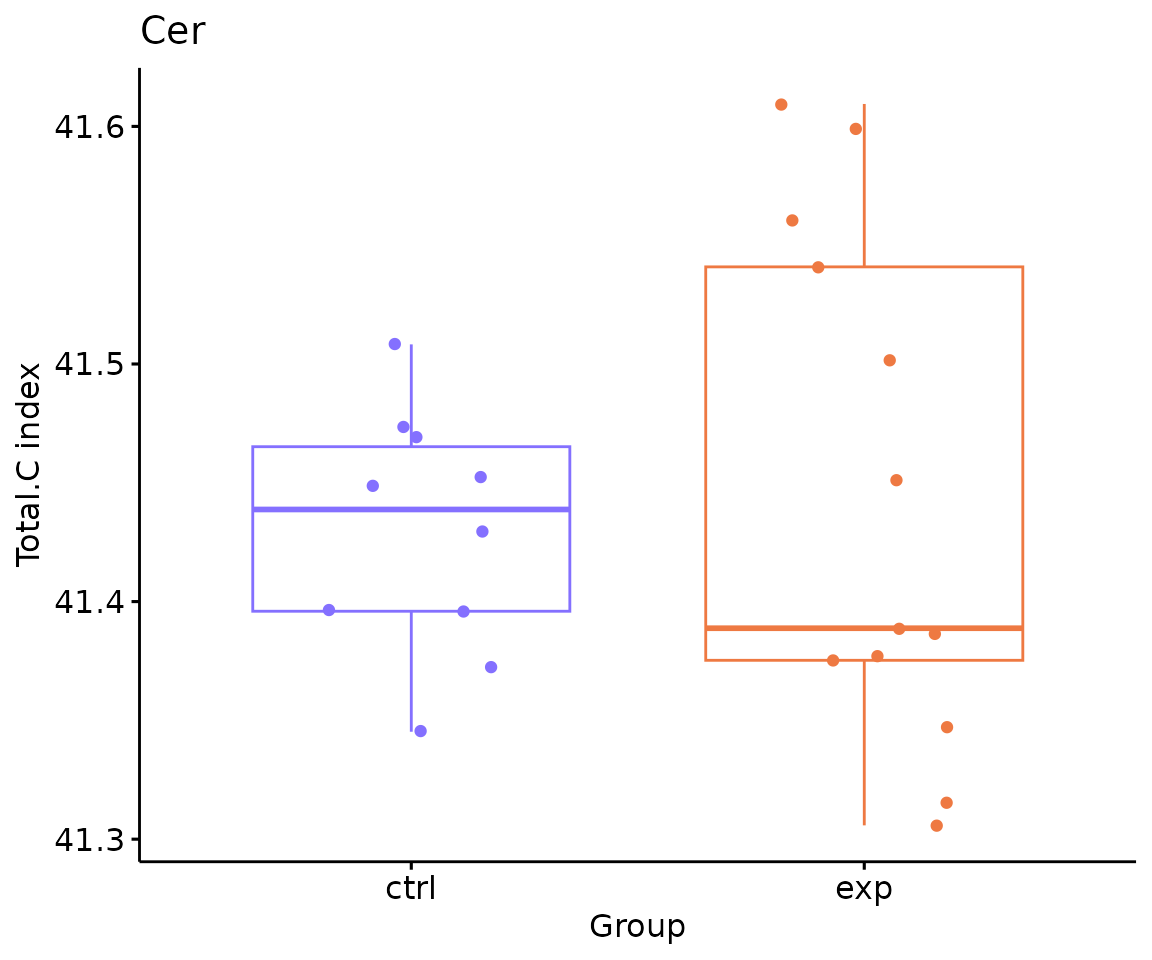
In the ‘Subgroup of characteristics’, besides the
selected characteristic in first section defined by parameter
char, we can further choose another characteristic by
parameter subChar. The two chosen characteristics,
char and subCharshould be either both
continuous data or one continuous and one categorical data.
- NOTE: You can use
LipidSigR::list_lipid_charto get all the selectable lipid characteristics. Please readvignette("1_tool_function").
# data processing
processed_se <- data_process(
se, exclude_missing=TRUE, exclude_missing_pct=70,
replace_na_method='min', replace_na_method_ref=0.5,
normalization='Percentage')
# subgroup differential expression of lipid characteristics
subChar_se <- subChar_twoGroup(
processed_se, char="Total.C", subChar="class", ref_group="ctrl",
test='t-test', significant="pval", p_cutoff=0.05,
FC_cutoff=1, transform='log10')
#> There are 4 ratio characteristics that can be converted in your dataset.After running the code, the returned subChar_se
contained the input abundance data, lipid characteristic table, group
information table, analysis results, and some some setting of input
parameters. You can view the data in subChar_se by
LipidSigR::extract_summarized_experiment.
# view differential expression of lipid characteristics
subChar_result <- extract_summarized_experiment(subChar_se)
# result summary
summary(subChar_result)
#> Length Class Mode
#> abundance 24 data.frame list
#> lipid_char_table 5 data.frame list
#> group_info 5 data.frame list
#> all_deChar_result 25 tbl_df list
#> sig_deChar_result 25 tbl_df list
#> processed_abundance 24 tbl_df list
#> char 1 -none- character
#> subChar 1 -none- character
#> significant 1 -none- character
#> p_cutoff 1 -none- numeric
#> FC_cutoff 1 -none- numericYou can also plot the results of a specific feature within the
subChar. For example, if you select “class” as
subChar, you can choose “Cer” within the ‘class’ feature by
parameter subChar_feature for plotting result plots.
(Note: Only static plots are displayed here.)
# get subChar_feature list
subChar_feature_list <- unique(
extract_summarized_experiment(subChar_se)$all_deChar_result$sub_feature)
# visualize subgroup differential expression of lipid characteristics
subChar_plot <- plot_subChar_twoGroup(subChar_se, subChar_feature="Cer")
# result summary
summary(subChar_plot)
#> Length Class Mode
#> static_barPlot 9 gg list
#> static_barPlot_sqrt 9 gg list
#> static_linePlot 9 gg list
#> static_linePlot_sqrt 9 gg list
#> static_boxPlot 10 gg list
#> interactive_barPlot 8 plotly list
#> interactive_barPlot_sqrt 8 plotly list
#> interactive_linePlot 8 plotly list
#> interactive_linePlot_sqrt 8 plotly list
#> interactive_boxPlot 8 plotly list
#> table_barPlot 11 tbl_df list
#> table_linePlot 11 tbl_df list
#> table_boxPlot 7 data.frame list
#> table_char_index 24 data.frame list
#> table_index_stat 13 grouped_df listThe results of ‘Subgroup of characteristics’ analysis in the second section
- Note: The star above the bar shows the significant difference of the specific subgroup of the selected characteristic between control and experimental groups.
# view result: bar plot of `subChar_feature`
subChar_plot$static_barPlot 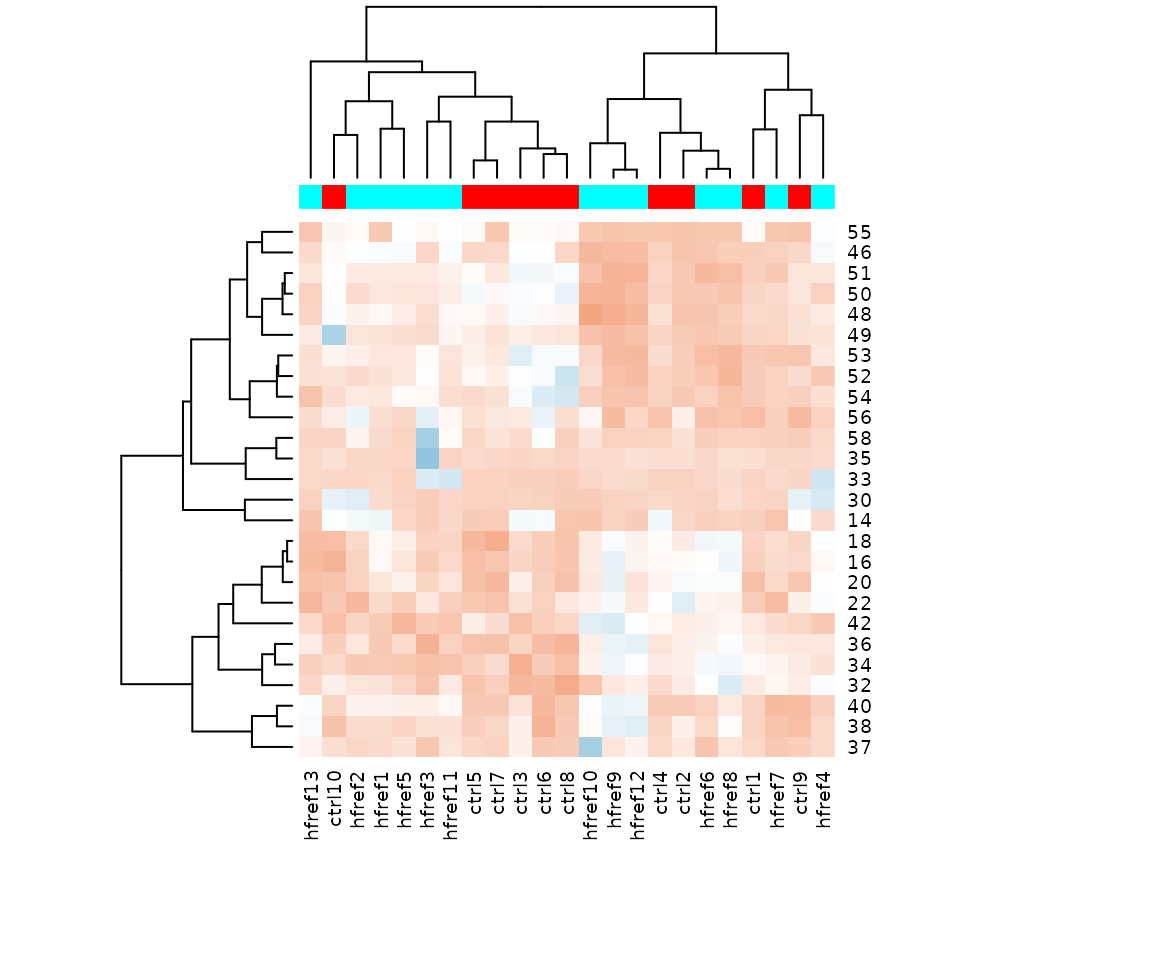
# view result: sqrt-scaled bar plot of `subChar_feature`
subChar_plot$static_barPlot_sqrt 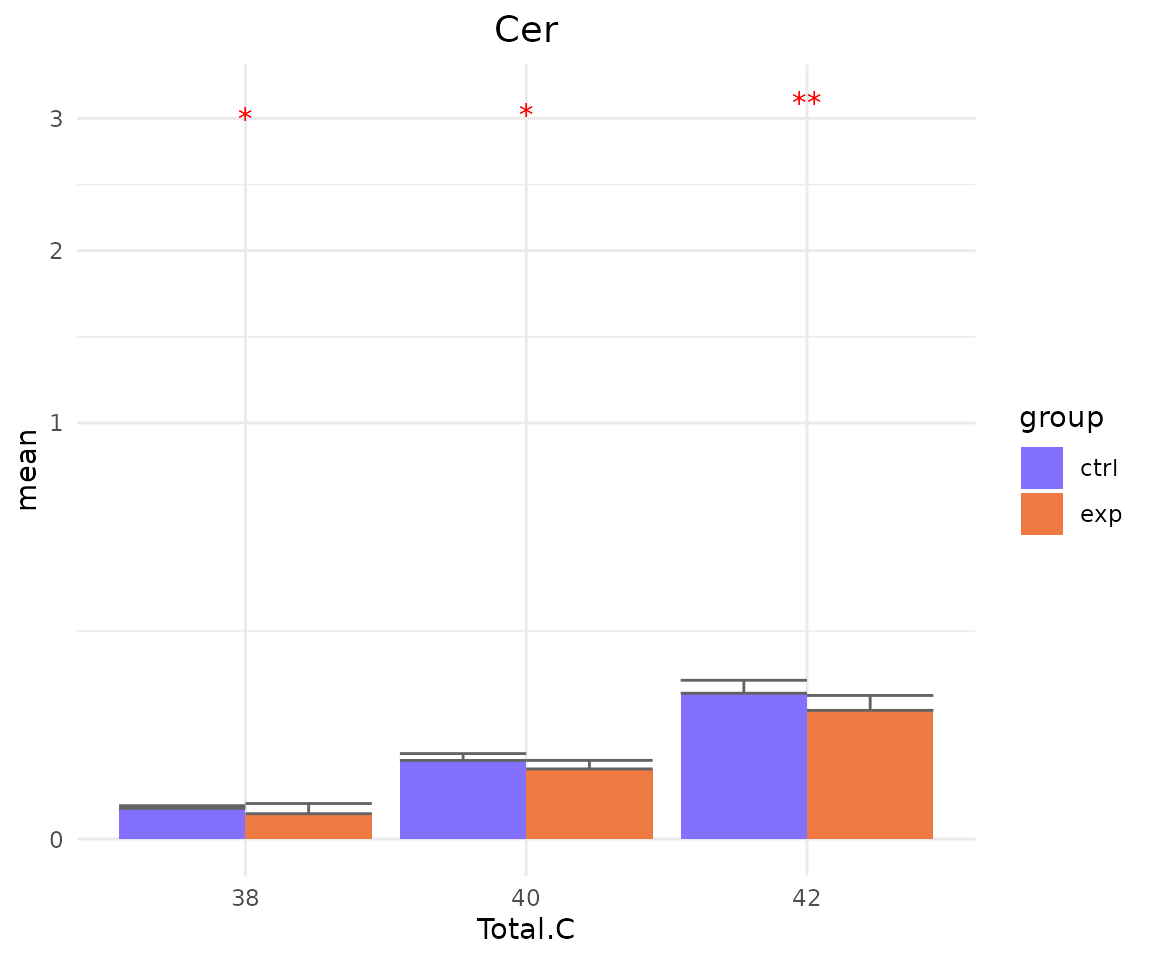
# view result: line plot of `subChar_feature`
subChar_plot$static_linePlot 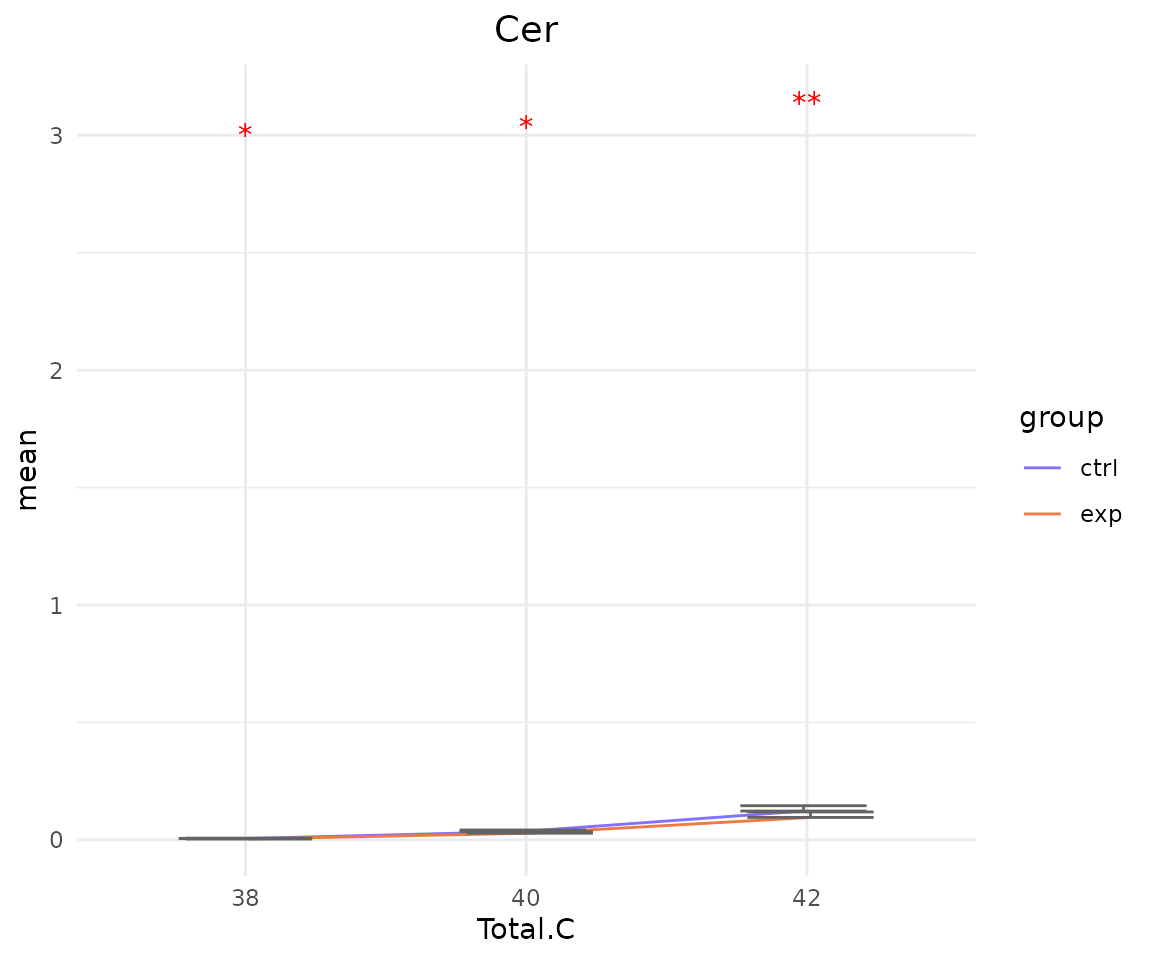
# view result: sqrt-scaled line plot of `subChar_feature`
subChar_plot$static_linePlot_sqrt 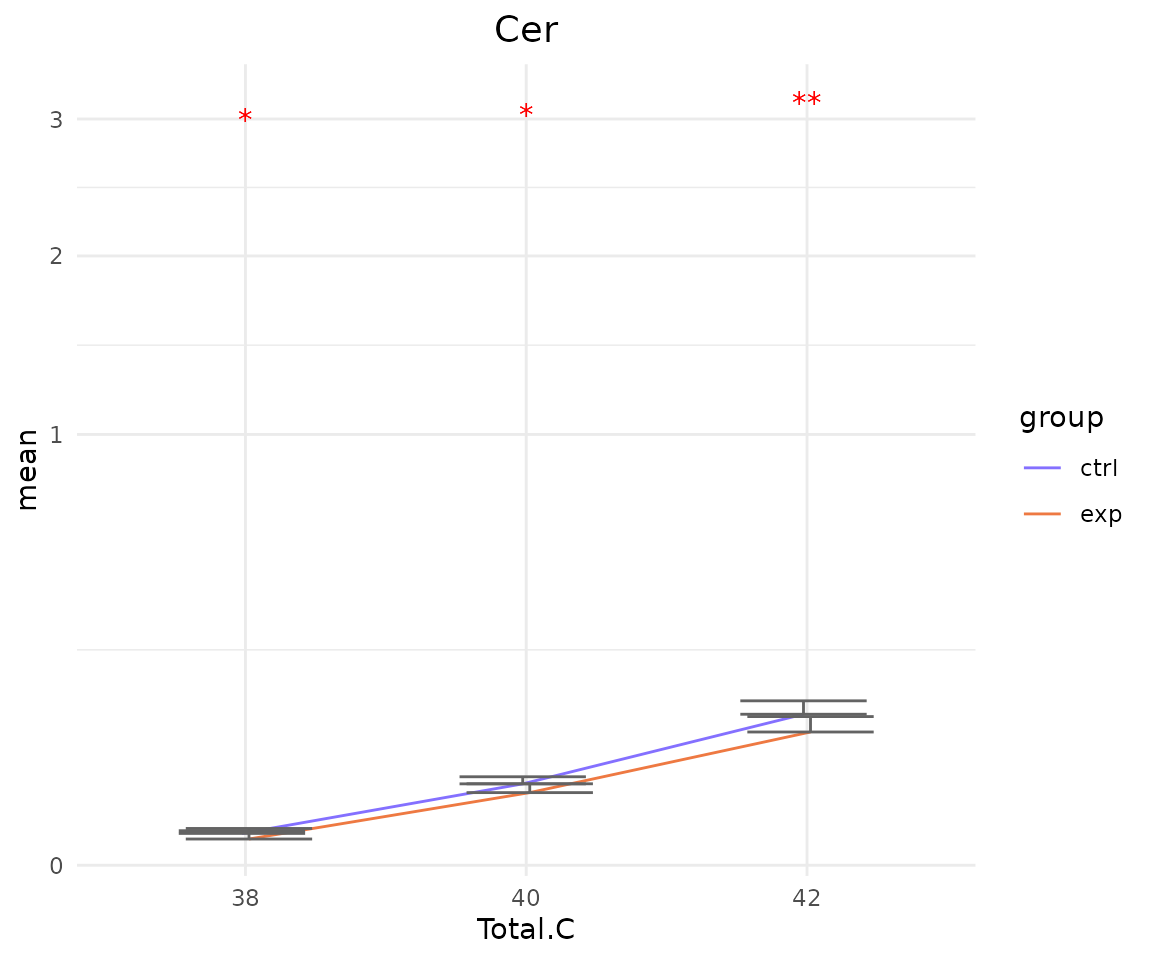
# view result: box plot of `subChar_feature`
subChar_plot$static_boxPlot 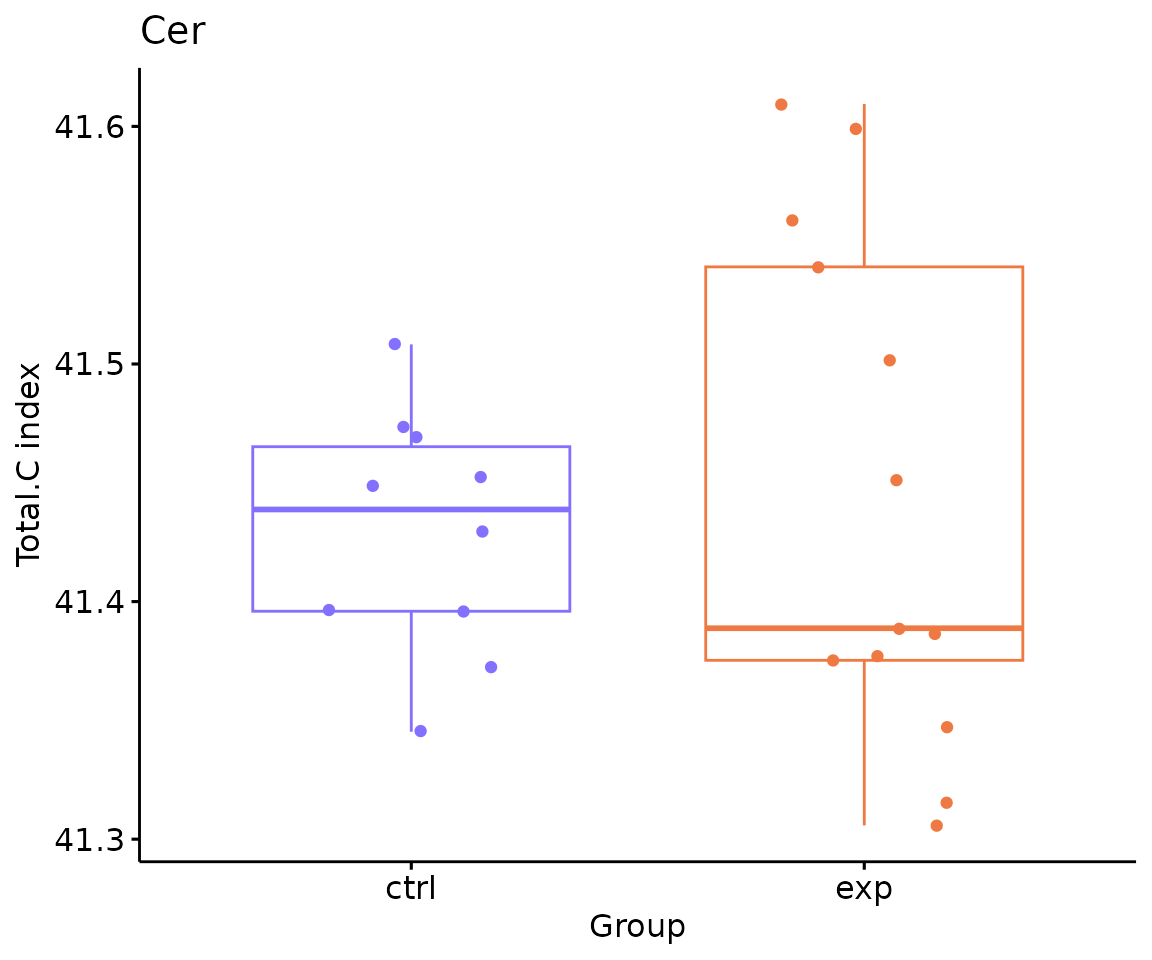
Dimension reduction
Dimension reduction is common when dealing with large numbers of observations and/or large numbers of variables in lipids analysis. It transforms data from a high-dimensional space into a low-dimensional space to retain vital properties of the original data and close to its intrinsic dimension.
Here, we provide 4 dimension reduction methods: PCA, t-SNE, UMAP, and PLS-DA.
The execution of all the functions respectively introduced in Section Section PCA, t-SNE, UMAP, and PLSDA. Links to there for more details manipulation.
The only difference is that the input data should be
deChar_se (output from lipid
characterisitcs analysis).
For example:
# conduct PLSDA
result_plsda <- dr_plsda(
deChar_se, ncomp=2, scaling=TRUE, clustering='group_info', cluster_num=2,
kmedoids_metric=NULL, distfun=NULL, hclustfun=NULL, eps=NULL, minPts=NULL)
# result summary
summary(result_plsda)
#> Length Class Mode
#> plsda_result 4 data.frame list
#> table_plsda_loading 2 data.frame list
#> interacitve_plsda 8 plotly list
#> interactive_loadingPlot 8 plotly list
#> static_plsda 9 gg list
#> static_loadingPlot 9 gg listHierarchical clustering
Hierarchical clustering can also be conducted based on the differential expression analysis results of lipid characteristics. It visualizes the differences of lipid characteristics between the control group and the experimental group.
- NOTE: The
charparameter should match the input used in thedeChar_twoGroupfrom lipid characteristics analysis
# conduct hierarchical clustering
result_hcluster <- heatmap_clustering(
de_se=deChar_se, char='Total.C', distfun='pearson',
hclustfun='complete', type='all')
#> char Total.C has been selected in upstream function.
# result summary
summary(result_hcluster)
#> Length Class Mode
#> interactive_heatmap 1 IheatmapHorizontal S4
#> static_heatmap 3 recordedplot list
#> corr_coef_matrix 598 -none- numeric
# view result: heatmap of significant lipid species
result_hcluster$static_heatmap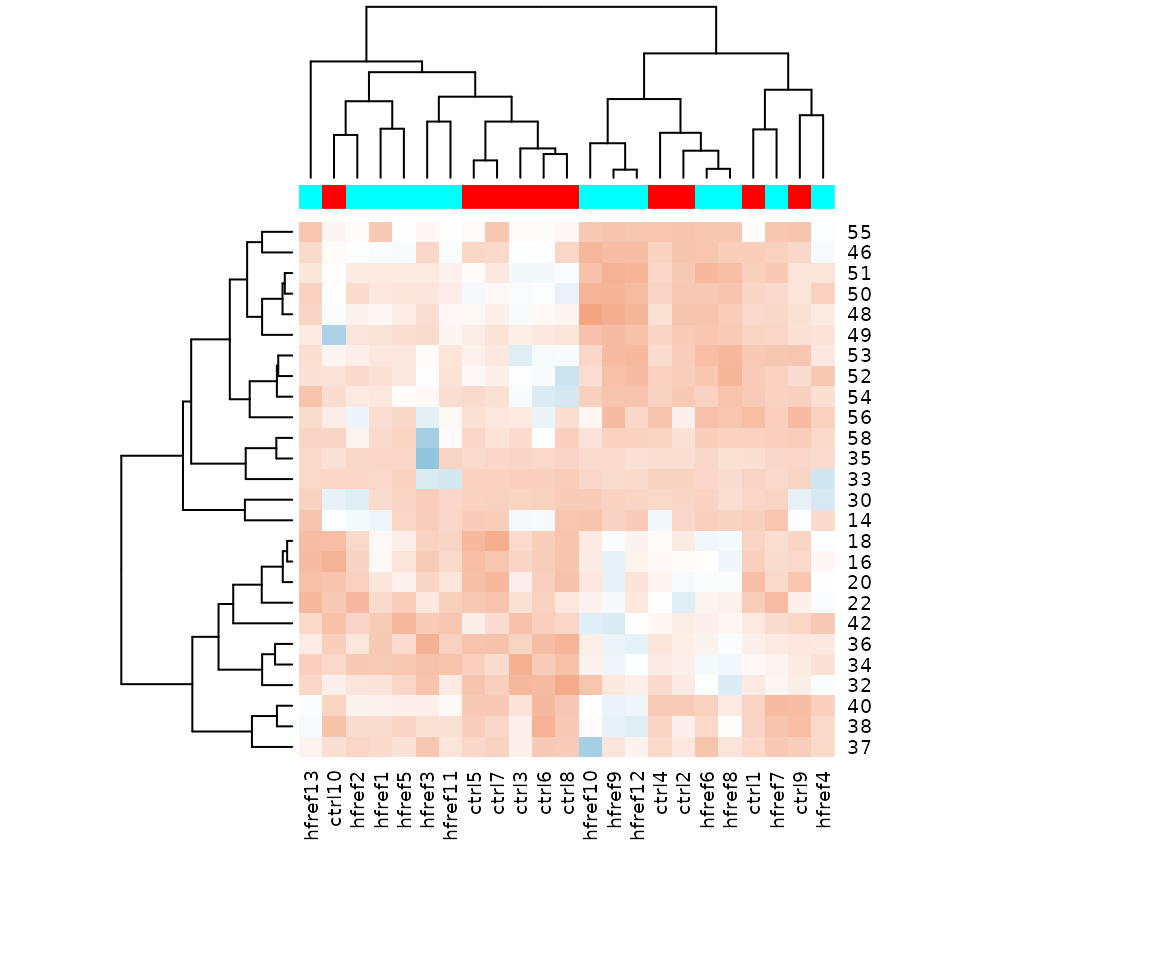
Heatmap of significant lipid species The difference between the two groups by observing the distribution of lipid species.
Double bond-chain length analysis analysis
This section provides heatmaps that illustrates the correlation between the double bond and chain length of lipid species. The color in the heatmaps is gradient according to log2FC.
The correlation is visually represented by cell colors—red indicates a positive correlation, while blue indicates a negative. Significant correlations are highlighted with an asterisk sign on the plot.
# data processing
processed_se <- data_process(
se, exclude_missing=TRUE, exclude_missing_pct=70,
replace_na_method='min', replace_na_method_ref=0.5,
normalization='Percentage')
# list lipid characteristics
list_lipid_char(processed_se)$chain_db_list
#> There are 4 ratio characteristics that can be converted in your dataset.
#> Lipid classification Lipid classification
#> "Category" "Main.Class"
#> Lipid classification Lipid classification
#> "Sub.Class" "class"
#> Physical or chemical properties Physical or chemical properties
#> "Bilayer.Thickness" "Bond.type"
#> Physical or chemical properties Physical or chemical properties
#> "Headgroup.Charge" "Intrinsic.Curvature"
#> Physical or chemical properties Physical or chemical properties
#> "Lateral.Diffusion" "Transition.Temperature"
#> Cellular component Function
#> "Cellular.Component" "Function"
# conduct double bond-chain length analysis (without setting `char_feature`)
heatmap_all <- heatmap_chain_db(
processed_se, char='class', char_feature=NULL, ref_group='ctrl',
test='t-test', significant='pval', p_cutoff=0.05,
FC_cutoff=1, transform='log10')
# result summary
summary(heatmap_all)
#> Length Class Mode
#> total_chain 5 -none- list
#> each_chain 5 -none- list
# summary of total chain result
summary(heatmap_all$total_chain)
#> Length Class Mode
#> static_heatmap 9 gg list
#> table_heatmap 21 data.frame list
#> processed_abundance 24 data.frame list
#> transformed_abundance 24 data.frame list
#> chain_db_se 86 SummarizedExperiment S4
# view result: heatmap of total chain
heatmap_all$total_chain$static_heatmap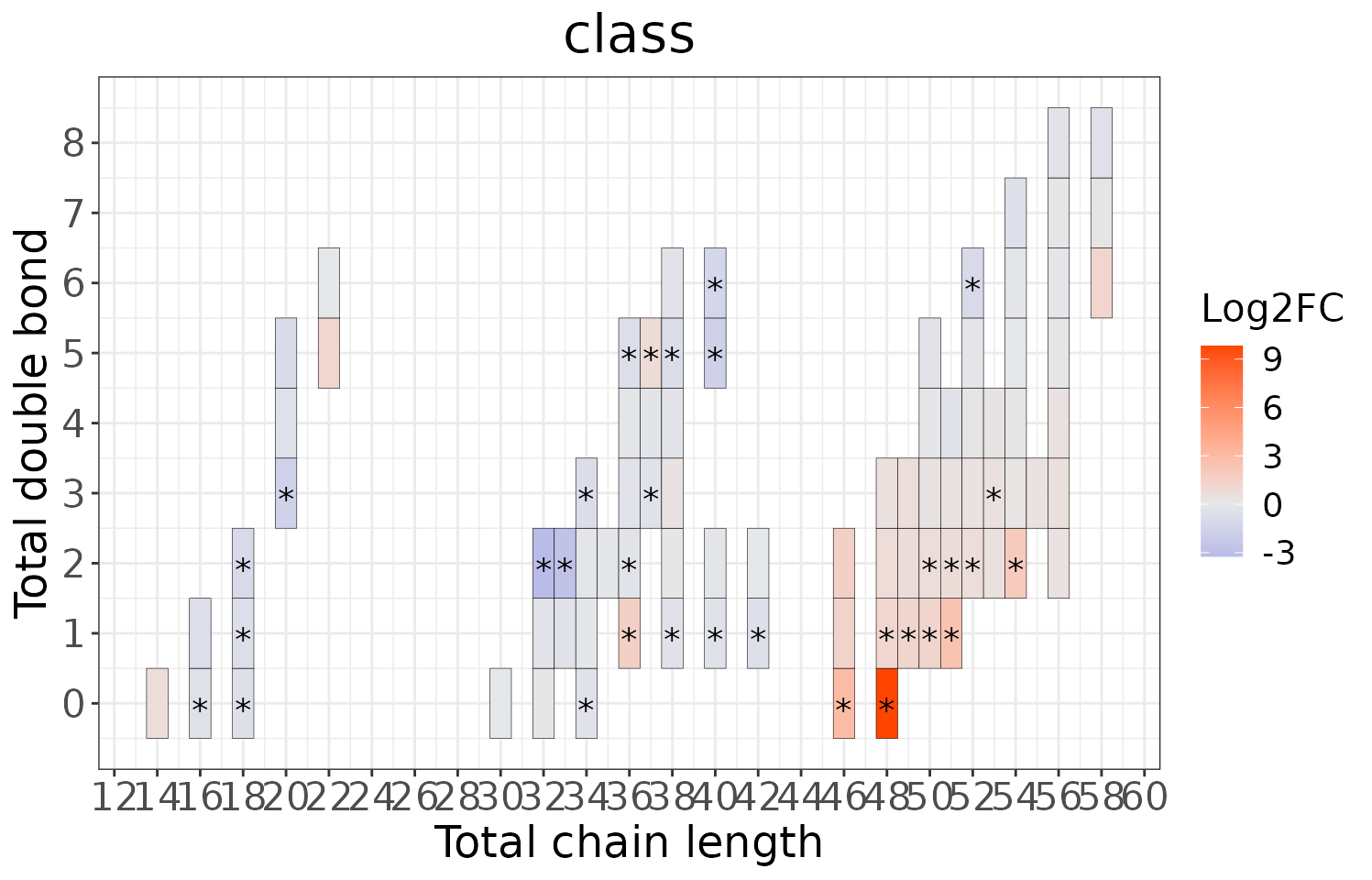
# summary of each chain result
summary(heatmap_all$each_chain)
#> Length Class Mode
#> static_heatmap 9 gg list
#> table_heatmap 21 data.frame list
#> processed_abundance 24 data.frame list
#> transformed_abundance 24 data.frame list
#> chain_db_se 19 SummarizedExperiment S4
# view result: heatmap of each chain
heatmap_all$each_chain$static_heatmap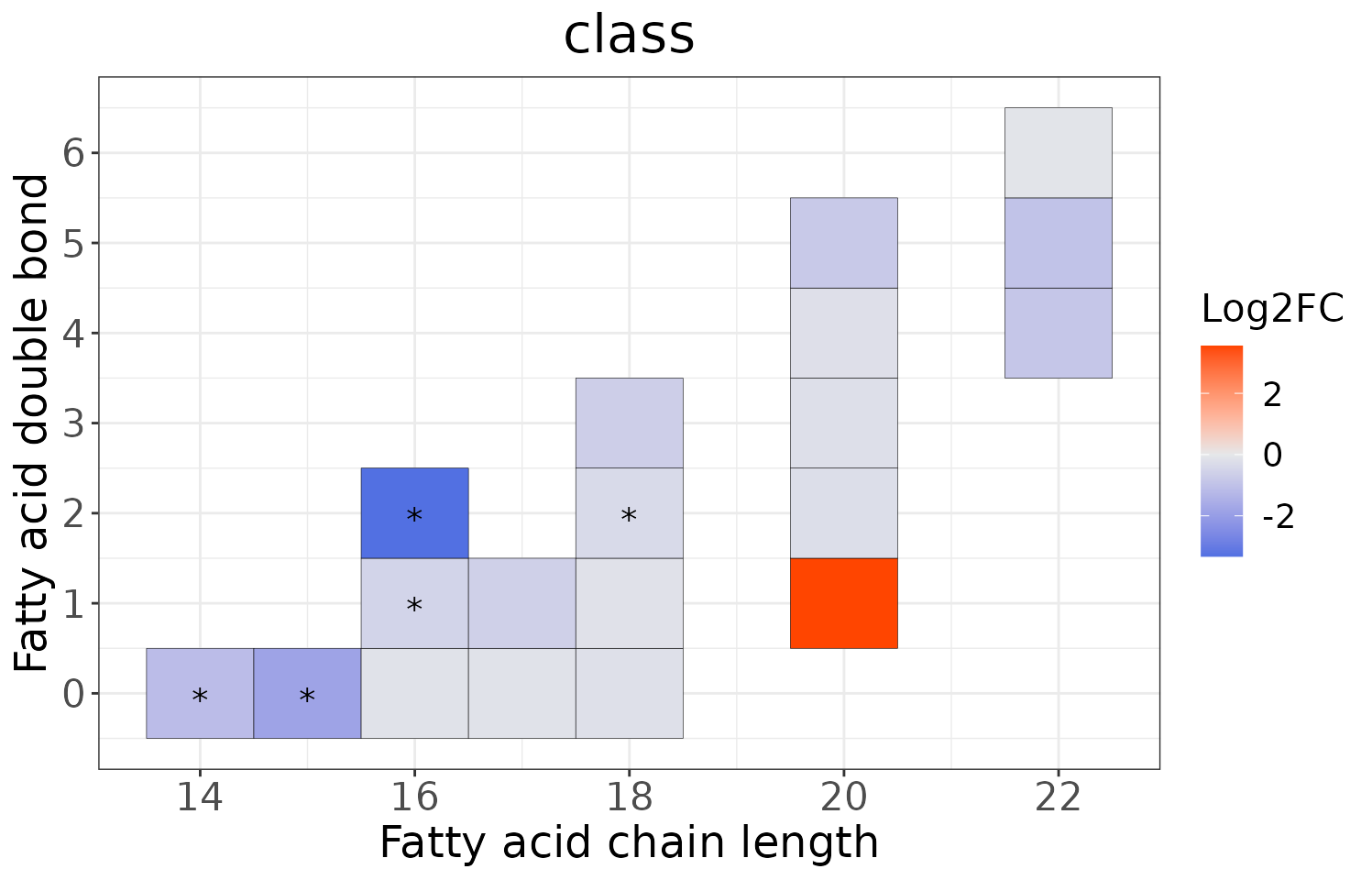
# conduct double bond-chain length analysis (a specific `char_feature`)
heatmap_one <- heatmap_chain_db(
processed_se, char='class', char_feature='PC', ref_group='ctrl',
test='t-test', significant='pval', p_cutoff=0.05,
FC_cutoff=1, transform='log10')
# result summary
summary(heatmap_one)
#> Length Class Mode
#> total_chain 5 -none- list
#> each_chain 5 -none- list
# summary of total chain result
summary(heatmap_one$total_chain)
#> Length Class Mode
#> static_heatmap 9 gg list
#> table_heatmap 22 data.frame list
#> processed_abundance 24 data.frame list
#> transformed_abundance 24 data.frame list
#> chain_db_se 25 SummarizedExperiment S4
# view result: heatmap of total chain
heatmap_one$total_chain$static_heatmap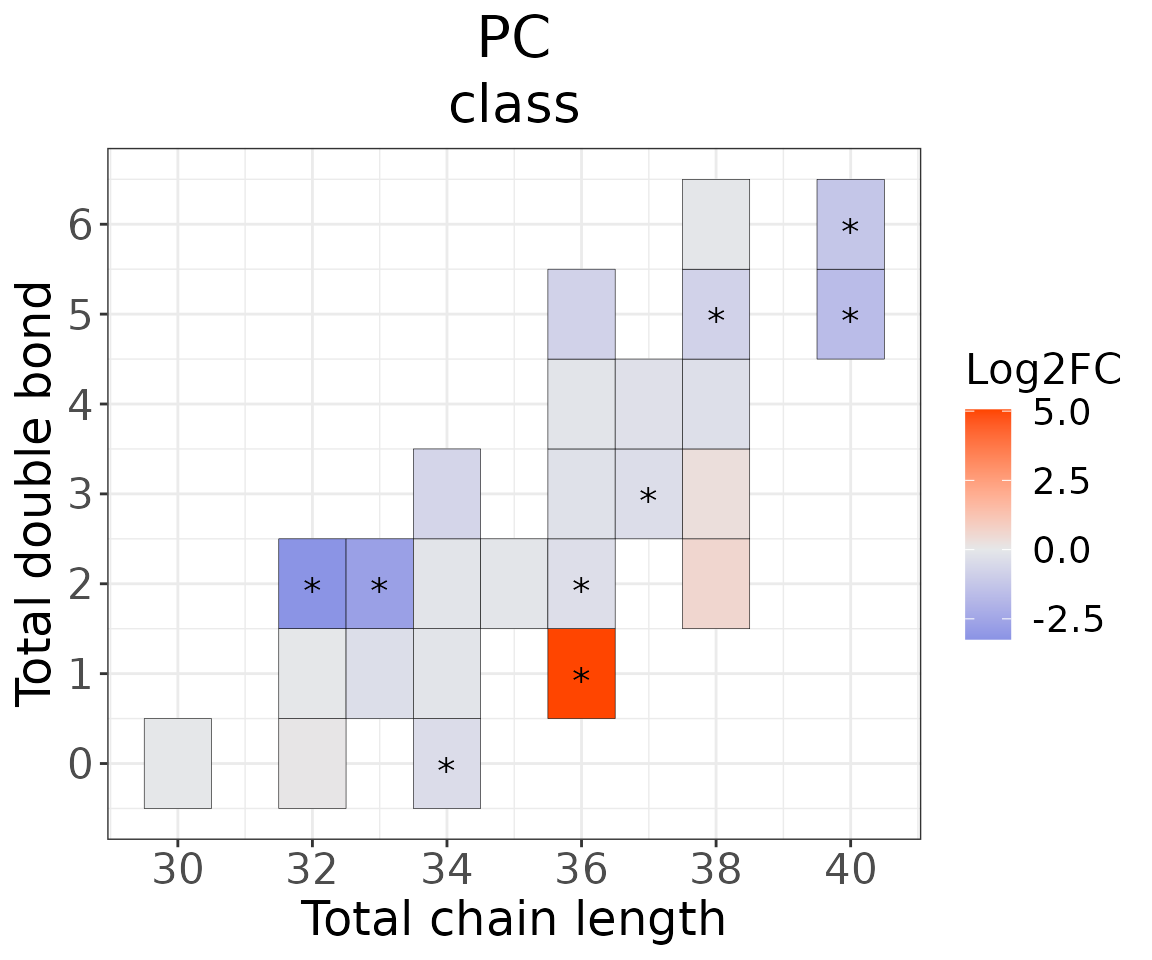
# summary of each chain result
summary(heatmap_one$each_chain)
#> Length Class Mode
#> static_heatmap 9 gg list
#> table_heatmap 22 data.frame list
#> processed_abundance 24 data.frame list
#> transformed_abundance 24 data.frame list
#> chain_db_se 18 SummarizedExperiment S4
# view result: heatmap of each chain
heatmap_one$each_chain$static_heatmap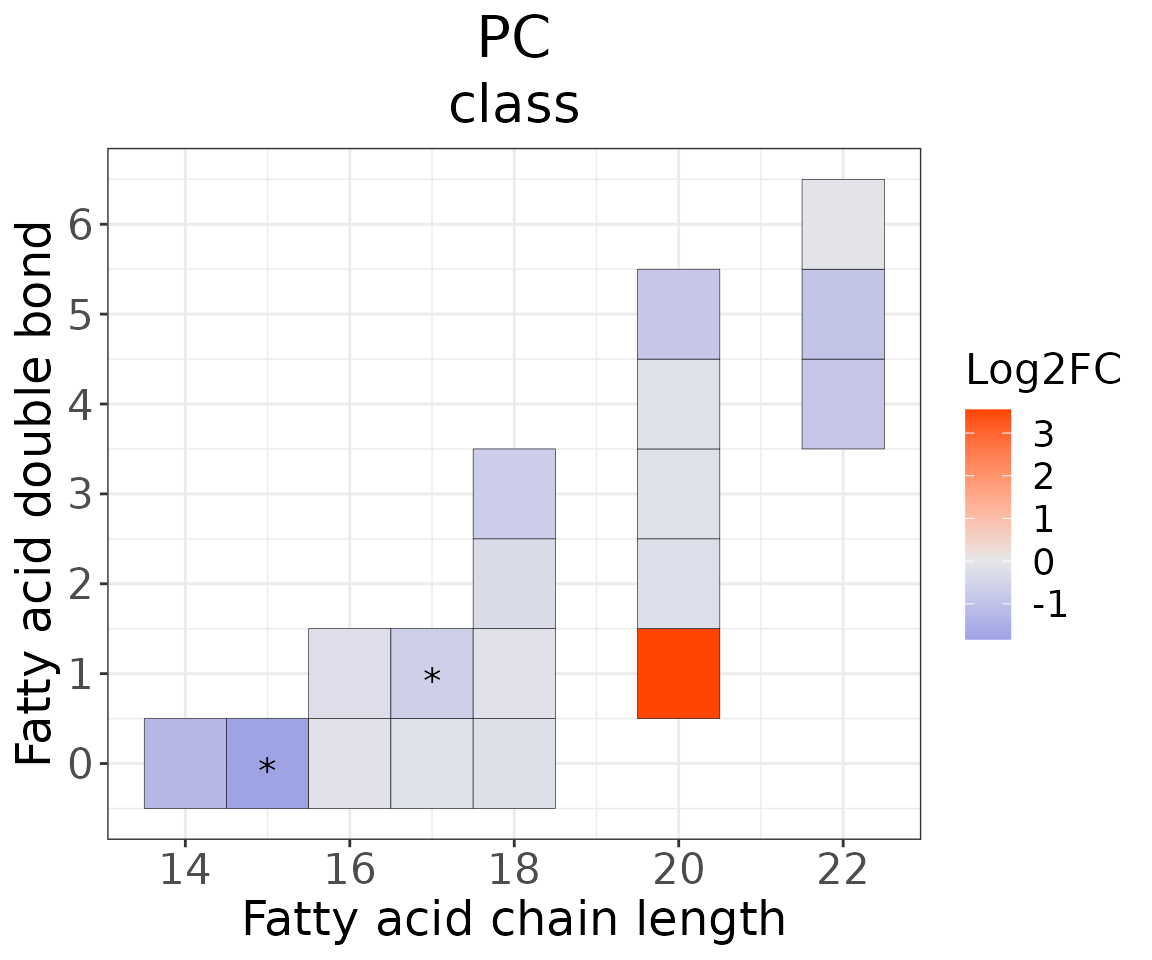
- NOTE: You can view the data in
chain_db_sebyLipidSigR::extract_summarized_experiment.
For example:
# view data in `chain_db_se`
heatmap_one_total_chain_list <-
extract_summarized_experiment(heatmap_one$each_chain$chain_db_se)
# result summary
summary(heatmap_one_total_chain_list)
#> Length Class Mode
#> abundance 24 data.frame list
#> lipid_char_table 4 data.frame list
#> group_info 4 data.frame listYou can further plot an abundance box plot for any lipid species of
interest by LipidSigR::boxPlot_feature_twoGroup.
For example, let’s use 15:0, a significant lipid species
from the heatmap above.
# plot abundance box plot of "15:0"
boxPlot_result <- boxPlot_feature_twoGroup(
heatmap_one$each_chain$chain_db_se, feature='15:0',
ref_group='ctrl', test='t-test', transform='log10')
# result summary
summary(boxPlot_result)
#> Length Class Mode
#> static_boxPlot 9 gg list
#> table_boxplot 7 data.frame list
#> table_stat 5 rstatix_test list
# view result: static box plot
boxPlot_result$static_boxPlot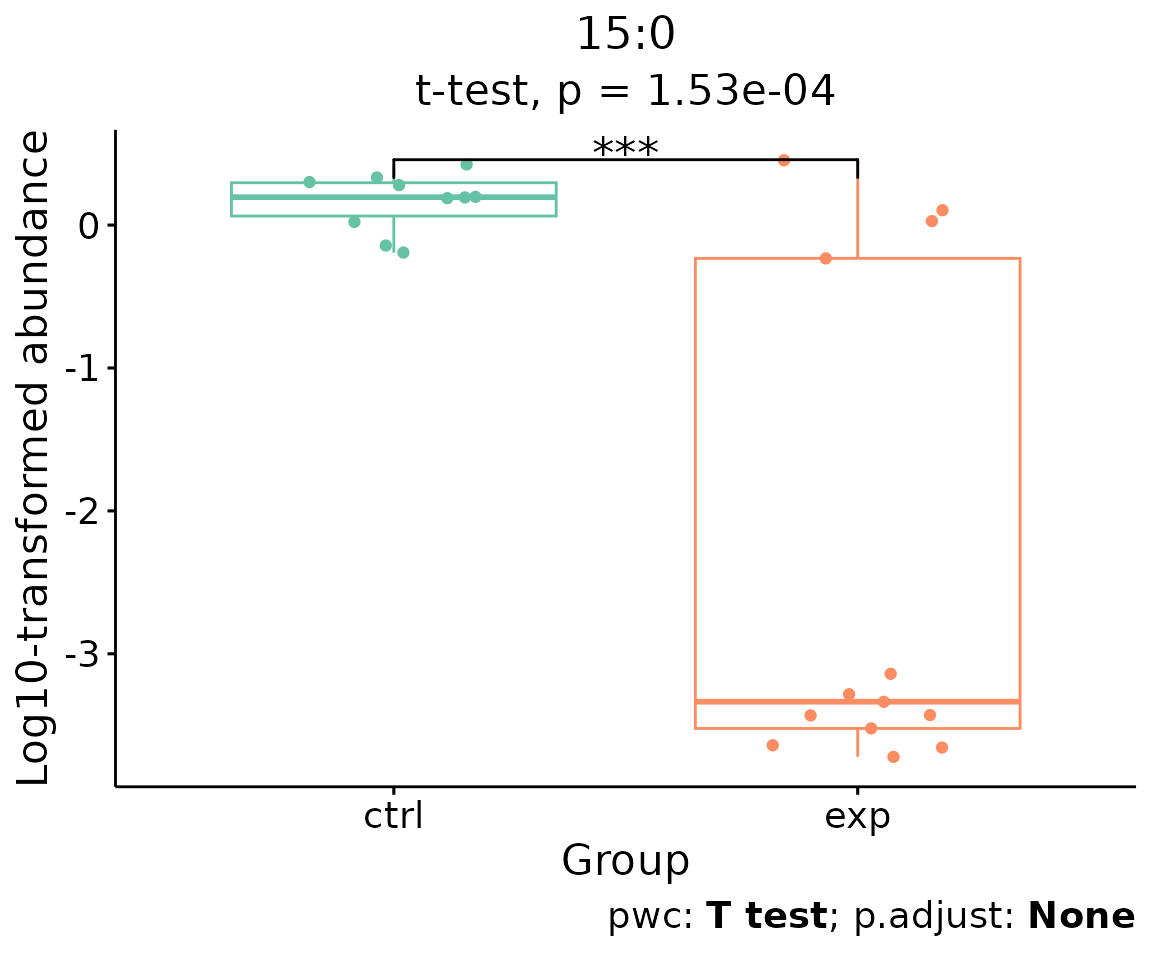
Box plot of lipid abundance An asterisk sign indicates significant differences between groups. The absence of an asterisk or line denotes a non-significant difference between groups.
Enrichment
Enrichment analysis provides two main approaches: ‘Over Representation Analysis (ORA)’ and ‘Lipid Set Enrichment Analysis (LSEA)’. ORA analysis illustrates significant lipid species enriched in the categories of lipid class. LSEA analysis is a computational method determining whether an a priori-defined set of lipids shows statistically significant, concordant differences between two biological states (e.g., phenotypes).
Over Representation Analysis (ORA)
The Over-Representation analysis provides whether significant lipid species are enriched in the categories of lipid class. Results are presented in tables and bar plots categorizing lipid species into ‘up-regulated’ or ‘down-regulated’ groups based on log2 fold change.
- NOTE: The input data of this section
deSp_seis generated bydeSp_twoGroupin lipid species analysis.
# conduct ORA
ora_all <- enrichment_ora(
deSp_se, char=NULL, significant='pval', p_cutoff=0.05)
# result summary
summary(ora_all)
#> Length Class Mode
#> enrich_result 14 tbl_df list
#> static_barPlot 9 gg list
#> interactive_barPlot 8 plotly list
#> table_barPlot 10 grouped_df list
# view result: ORA bar plot
ora_all$static_barPlot 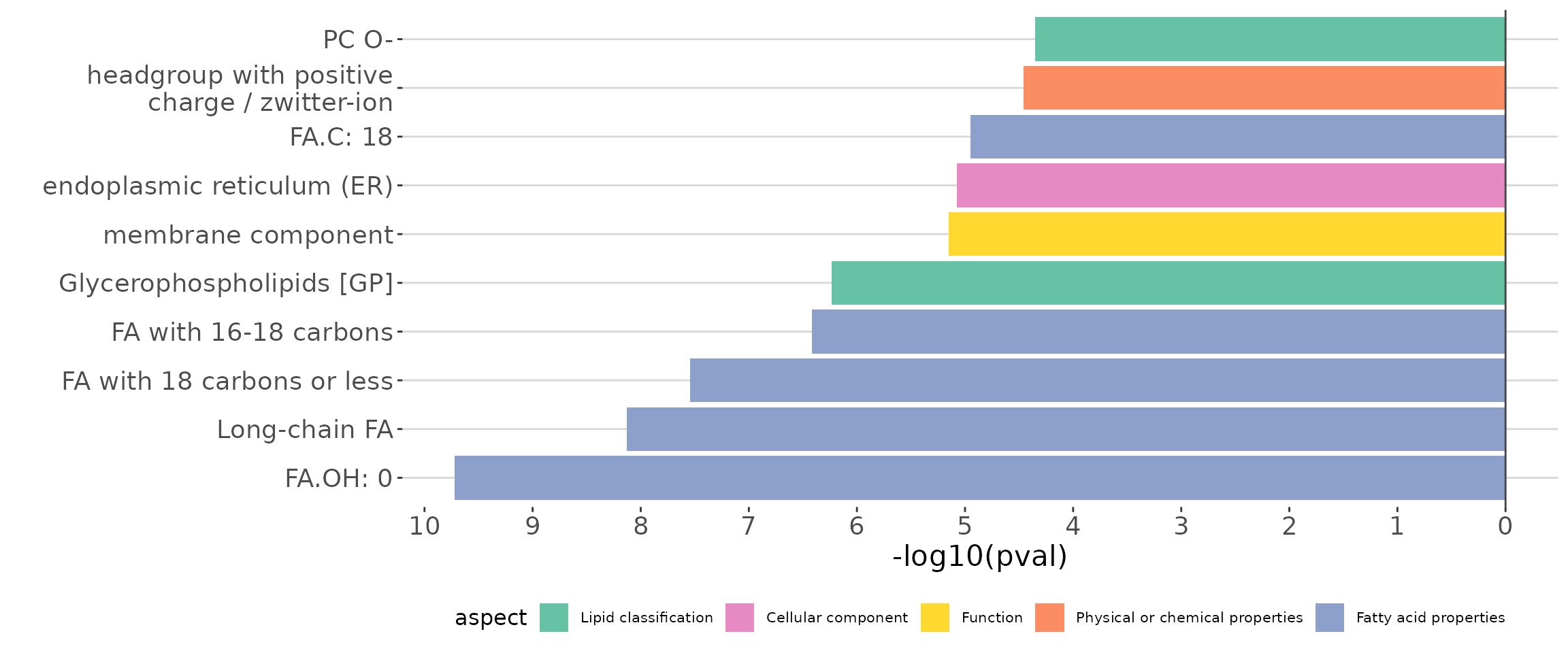
ORA bar plot of all characteristics The bar plot shows the top 10 significant up-regulated and down-regulated terms.
# list available lipid characteristics
list_lipid_char(processed_se)$common_list
#> There are 4 ratio characteristics that can be converted in your dataset.
#> Lipid classification Lipid classification
#> "Category" "Main.Class"
#> Lipid classification Lipid classification
#> "Sub.Class" "class"
#> Fatty acid properties Fatty acid properties
#> "FA" "FA.C"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category1" "FA.Chain.Length.Category2"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category3" "FA.DB"
#> Fatty acid properties Fatty acid properties
#> "FA.OH" "FA.Unsaturation.Category1"
#> Fatty acid properties Fatty acid properties
#> "FA.Unsaturation.Category2" "Total.C"
#> Fatty acid properties Fatty acid properties
#> "Total.DB" "Total.FA"
#> Fatty acid properties Physical or chemical properties
#> "Total.OH" "Bilayer.Thickness"
#> Physical or chemical properties Physical or chemical properties
#> "Bond.type" "Headgroup.Charge"
#> Physical or chemical properties Physical or chemical properties
#> "Intrinsic.Curvature" "Lateral.Diffusion"
#> Physical or chemical properties Cellular component
#> "Transition.Temperature" "Cellular.Component"
#> Function
#> "Function"
# conduct ORA of a specific `char`
ora_one <- enrichment_ora(
deSp_se, char='class', significant='pval', p_cutoff=0.05)
# result summary
summary(ora_one)
#> Length Class Mode
#> enrich_result 14 tbl_df list
#> static_barPlot 9 gg list
#> interactive_barPlot 8 plotly list
#> table_barPlot 11 grouped_df list
# view result: ORA bar plot
ora_one$static_barPlot 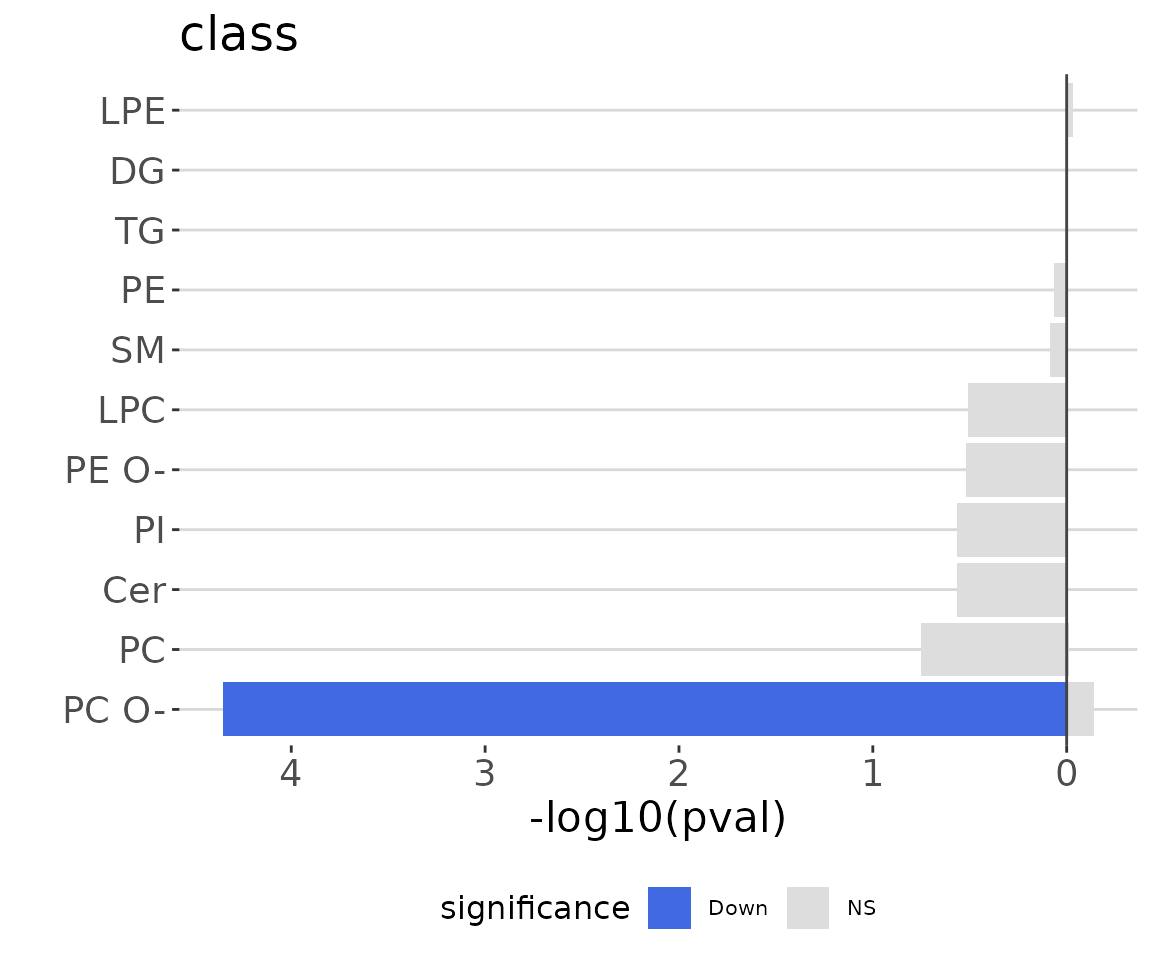
ORA bar plot of specific characteristics The bar plot classifies significant lipid species into ‘up-regulated’ or ‘down-regulated’ categories based on their log2 fold change, according to a selected characteristic. Red bars indicate up-regulated, blue bars represent down-regulated, and grey bars signify non-significant.
Lipid Set Enrichment Analysis (LSEA)
Lipid Set Enrichment Analysis (LSEA) is a computational method determining whether an a priori-defined set of lipids shows statistically significant, concordant differences between two biological states (e.g., phenotypes). Results are presented in tables and bar plots categorizing lipid species into ‘up-regulated’ or ‘down-regulated’ groups based on NES (Normalized Enrichment Score), and a table.
- NOTE: The input data of this section
deSp_seis generated bydeSp_twoGroupin lipid species analysis.
# conduct LSEA
lsea_all <- enrichment_lsea(
deSp_se, char=NULL, rank_by='statistic', significant='pval',
p_cutoff=0.05)
# result summary
summary(lsea_all)
#> Length Class Mode
#> enrich_result 11 tbl_df list
#> static_barPlot 9 gg list
#> interactive_barPlot 8 plotly list
#> table_barPlot 8 tbl_df list
#> lipid_set 167 -none- list
#> ranked_list 182 -none- numeric
# view result: LSEA bar plot
lsea_all$static_barPlot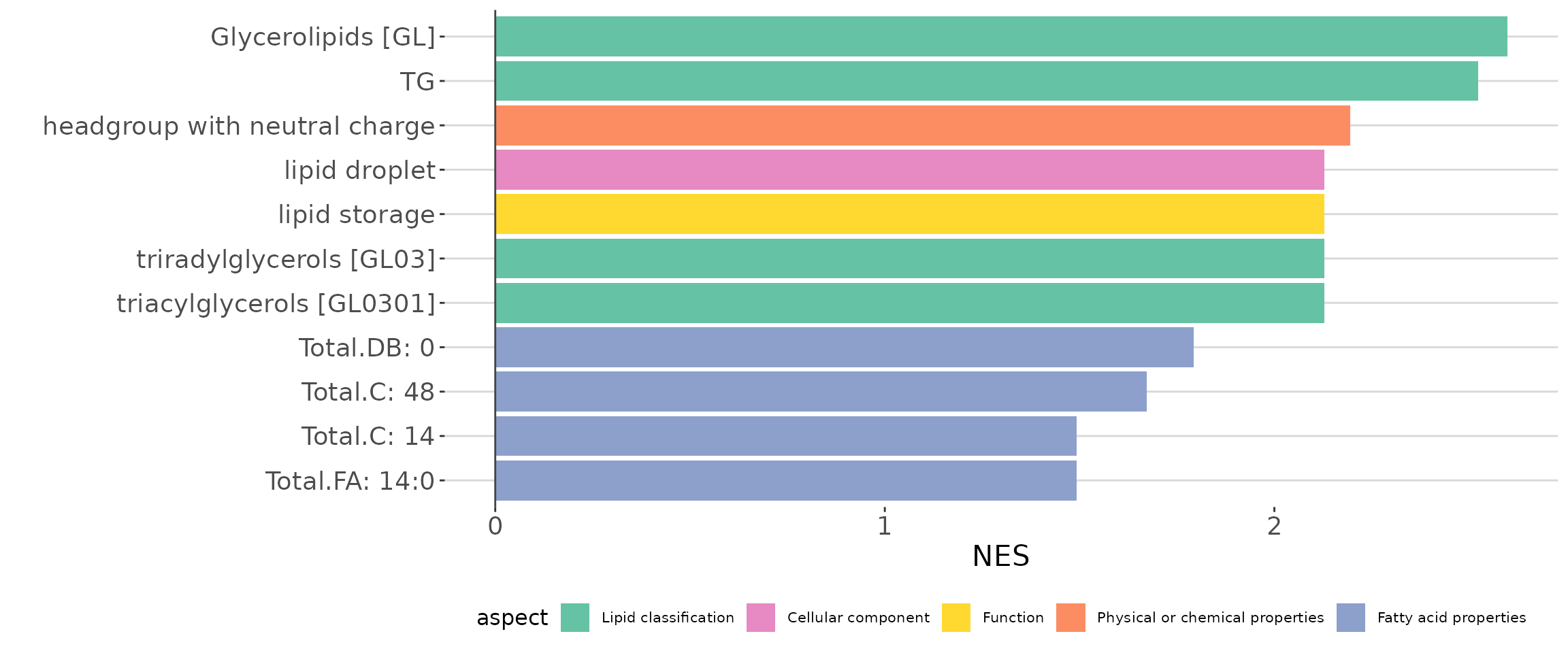
LSEA bar plot of all characteristics The bar plot shows the top 10 significant up-regulated and down-regulated terms.
# list available lipid characteristics
list_lipid_char(processed_se)$common_list
#> There are 4 ratio characteristics that can be converted in your dataset.
#> Lipid classification Lipid classification
#> "Category" "Main.Class"
#> Lipid classification Lipid classification
#> "Sub.Class" "class"
#> Fatty acid properties Fatty acid properties
#> "FA" "FA.C"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category1" "FA.Chain.Length.Category2"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category3" "FA.DB"
#> Fatty acid properties Fatty acid properties
#> "FA.OH" "FA.Unsaturation.Category1"
#> Fatty acid properties Fatty acid properties
#> "FA.Unsaturation.Category2" "Total.C"
#> Fatty acid properties Fatty acid properties
#> "Total.DB" "Total.FA"
#> Fatty acid properties Physical or chemical properties
#> "Total.OH" "Bilayer.Thickness"
#> Physical or chemical properties Physical or chemical properties
#> "Bond.type" "Headgroup.Charge"
#> Physical or chemical properties Physical or chemical properties
#> "Intrinsic.Curvature" "Lateral.Diffusion"
#> Physical or chemical properties Cellular component
#> "Transition.Temperature" "Cellular.Component"
#> Function
#> "Function"
# conduct LSEA of a specific `char`
lsea_one <- enrichment_lsea(
deSp_se, char='class', rank_by='log2FC',
significant='pval', p_cutoff=0.05)
# result summary
summary(lsea_one)
#> Length Class Mode
#> enrich_result 11 tbl_df list
#> static_barPlot 9 gg list
#> interactive_barPlot 8 plotly list
#> table_barPlot 9 tbl_df list
#> lipid_set 11 -none- list
#> ranked_list 182 -none- numeric
# view result: LSEA bar plot
lsea_one$static_barPlot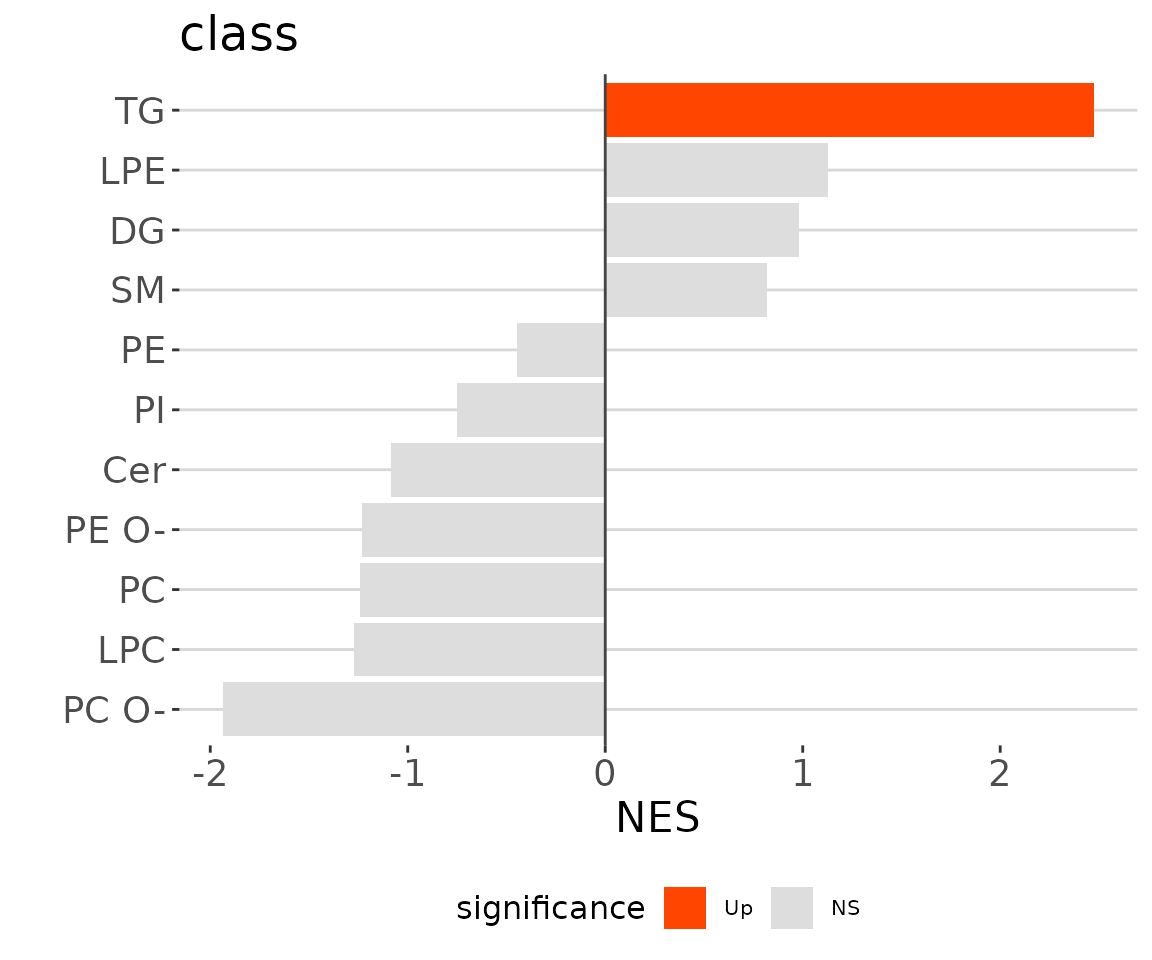
LSEA bar plot of a specific char The
bar plot classifies significant lipid species into ‘up-regulated’ or
‘down-regulated’ categories based on their log2 fold change, according
to a selected characteristic. Red bars indicate up-regulated, blue bars
represent down-regulated, and grey bars signify non-significant.
After running enrichment_lsea, you can continue
executing plot_enrichment_lsea to plot the enrichment plot
further. Please use the whole output of enrichment_lsea as
the input for plotting.
# plot LSEA results
lsea_plot <- plot_enrichment_lsea(
lsea_res=lsea_one, char='class', char_feature='TG')
# view result: enrichment plot
lsea_plot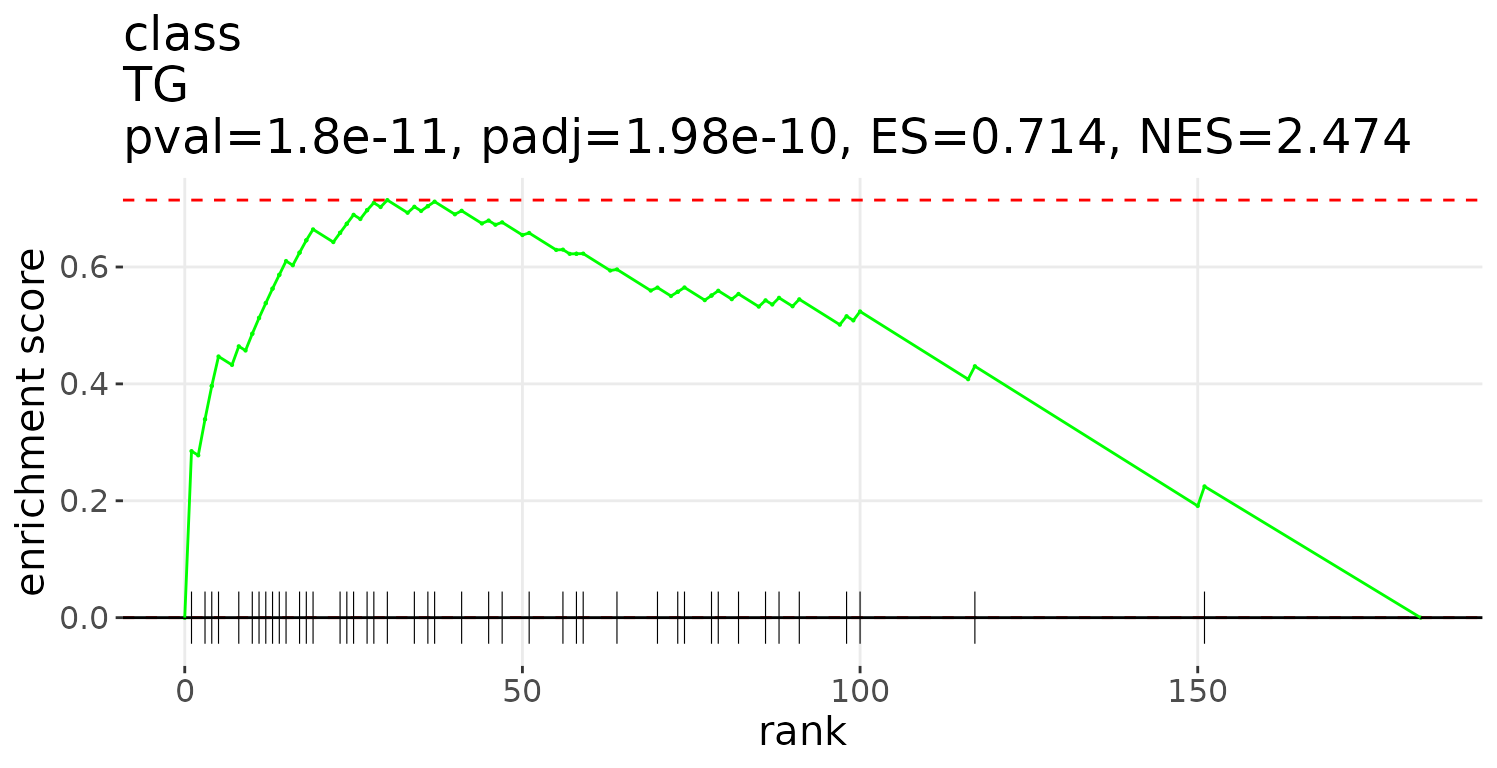
Network
This section provides three functions to quickly generate input data for constructing networks. After running the corresponding function, you will obtain the input data for a specific network. The available networks include the Pathway Activity Network, Lipid Reaction Network, and GATOM Network. Detailed instructions for each are described in the following sections.
- NOTE: The input data of this section
deSp_seis generated bydeSp_twoGroupin lipid species analysis.
Pathway activity network
The network provides activity pathways among lipid classes.
Follow the instructions below to get the input data for constructing the network.
# generate table for constructing Pathway activity network
network_table <- nw_pathway_activity(deSp_se, organism='mouse')
# result summary
summary(network_table)
#> Length Class Mode
#> table_edge 11 data.frame list
#> table_node 9 tbl_df list
#> table_pathway_score 4 grouped_df list
#> table_zScore 8 data.frame listAfter obtaining all the returned tables, you can use them to
construct a network. Here, we use the visNetwork package to
display an example.
# network visualization
library(visNetwork)
network <- visNetwork(
nodes=network_table$table_node, edges=network_table$table_edge) %>%
visLayout(randomSeed=500) %>%
visPhysics(
solver='barnesHut', stabilization=TRUE,
barnesHut=list(gravitationalConstant=-3000)) %>%
visInteraction(navigationButtons=TRUE) %>%
visEvents(
dragEnd="function () {this.setOptions( { physics: false } );}") %>%
visEdges(color=list(color="#DDDDDD",highlight="#C62F4B")) %>%
visOptions(
highlightNearest=list(enabled=TRUE, degree=1, hover=FALSE),
selectedBy="group", nodesIdSelection=TRUE)
# view network
networkLipid reaction network
This network illustrates the important reactions of differentially expressed lipid classes and species.
Follow the instructions below to get the input data for constructing the network.
# generate table for constructing Lipid reaction network
network_table <- nw_lipid_reaction(
deSp_se, organism='mouse', show_sp='sigClass', show_all_reactions=FALSE,
sp_significant='pval', sp_p_cutoff=0.05, sp_FC_cutoff=1,
class_significant='pval', class_p_cutoff=0.05, class_FC_cutoff=1)
# result summary
summary(network_table)
#> Length Class Mode
#> table_edge 11 data.table list
#> table_node 9 data.table list
#> table_reaction 4 data.frame list
#> table_stat 4 data.frame listAfter obtaining all the returned tables, you can use them to
construct a network. Here, we use the visNetwork package to
display an example.
library(visNetwork)
# network visualization
network <- visNetwork(
nodes=network_table$table_node, edges=network_table$table_edge) %>%
visLayout(randomSeed=500) %>%
visPhysics(
solver='barnesHut', stabilization=TRUE,
barnesHut=list(gravitationalConstant=-2500)) %>%
visInteraction(navigationButtons=TRUE) %>%
visEvents(
dragEnd="function () {this.setOptions( { physics: false } );}") %>%
visOptions(
highlightNearest=list(enabled=TRUE, degree=1, hover=FALSE),
selectedBy="group", nodesIdSelection=TRUE)
# view network
networkGATOM network
The network shows the important reactions of differentially expressed lipid species.
Follow the instructions below to get the input data for constructing the network.
# generate table for constructing GATOM network
network_table <- nw_gatom(
deSp_se, organism='mouse', n_lipid=50, sp_significant='pval',
sp_p_cutoff=0.05, sp_FC_cutoff=1)
#> Registered S3 method overwritten by 'GGally':
#> method from
#> +.gg ggplot2
#> Found DE table for metabolites with Species IDs
#> Metabolite p-value threshold: 1.000000
#> Metabolite BU alpha: 0.043884
#> FDR for metabolites: 0.043894
# result summary
summary(network_table)
#> Length Class Mode
#> table_edge 17 data.table list
#> table_node 12 data.table list
#> table_reaction 4 data.table list
#> table_stat 3 data.table listAfter obtaining all the returned tables, you can use them to
construct a network. Here, we use the visNetwork package to
display an example.
library(visNetwork)
# network visualization
network <- visNetwork(
nodes=network_table$table_node, edges=network_table$table_edge) %>%
visLayout(randomSeed=500) %>%
visPhysics(
solver='barnesHut', stabilization=TRUE,
barnesHut=list(gravitationalConstant=-3000)) %>%
visInteraction(navigationButtons=TRUE) %>%
visEvents(
dragEnd="function () {this.setOptions( { physics: false } );}") %>%
visEdges(color=list(color="#DDDDDD",highlight="#C62F4B")) %>%
visOptions(
highlightNearest=list(enabled=TRUE, degree=1, hover=FALSE),
selectedBy="group", nodesIdSelection=TRUE)
# view network
networkMachine learning
“Machine learning” provides many feature selection methods and classifiers for building binary classification models. Additionally, several following analyses help users evaluate algorithm performance and identify key lipid-related variables.
To conduct machine learning analysis, the data must include at least 60 samples, and the group information table format differs from the analyses mentioned in the previous workflows. Since the example dataset used in previous workflows contains only 23 samples, if you want to continue the machine learning analysis, changing the example dataset is needed. See the details of input data preparation in Data praparation. This dataset consists of Group 0 (N = 114) and Group 1 (N = 114).
Model construction
In the machine learning section, we will apply various feature selection methods and assess each feature’s importance. Data on lipid species and lipid characteristics will be combined to predict a binary outcome using multiple machine-learning approaches, allowing us to identify the optimal feature combination for further analysis. Monte Carlo cross-validation (MCCV) will be used to evaluate model performance and achieve statistical significance.
Each cross-validation run randomly divides the data into training and
testing sets. The training data is used to select the top 2, 3, 5, 10,
20, 50, or 100 important features for model training. The model is then
validated using the testing data. If the dataset contains fewer than 100
features, the maximum number of features is set to the total available.
The proportion of data used for testing and the number of
cross-validation iterations can be defined by the parameters
split_prop and nfold, respectively. (Note:
Increasing the number of cross-validation iterations will result in
longer computation times.)
Feature selection methods are designed to identify and rank the most
important variables for predicting the target outcome. Our platform
offers two categories of feature selection methods: univariate and
multivariate analysis. In univariate analysis, methods such as p-value,
p-value*Fold Change, and ROC are used to compare each feature between
two groups. The user can set the criteria for ranking the features.
Based on users’ settings, the top N features are chosen using metrics
like -log10(p-value), -log10(p-value)*Fold Change, or the Area Under
Curve (AUC). For multivariate analysis, we provide options including
Random Forest, Linear SVM (e1071), Lasso
(glmnet), Ridge (glmnet), and ElasticNet
(glmnet). Random Forest (ranger) utilizes
built-in feature importance metrics, while the other methods rank
features based on the absolute values of their coefficients. (Note:
The names in parentheses indicate the software packages used.)
The provided 8 feature ranking methods and 6 classification methods for training and selecting the best model are listed below.
1. Feature ranking methods: p-value, p-value*FC, ROC, Random Forest, Linear SVM, Lasso, Ridge, ElasticNet.
2. Classification methods: Random Forest, Linear SVM, Lasso, Ridge, ElasticNet, XGBoost.After constructing the model, a series of consequent analyses can be conducted to evaluate the methods and visualize machine learning results, including ROC/PR curve, model predictivity, sample probability, feature importance, and network.
Let us begin by building the model. We will use the
SummarizedExperiment object ml_input as the input data. For
instructions on constructing the input SummarizedExperiment object,
please refer to Data preparation.
# data processing
processed_ml <- data_process(
ml_input, exclude_missing=TRUE, exclude_missing_pct=70,
replace_na_method='min', replace_na_method_ref=0.5,
normalization='Percentage')
# lipid characteristic
char_list <- list_lipid_char(processed_ml)
# construct machine learning model
ml_se <- ml_model(
processed_ml, char=c("class","Total.DB"), transform='log10',
ranking_method='Random_forest', ml_method='Random_forest',
split_prop=0.3, nfold=10, alpha=NULL)
#> Processing CV fold 1
#> Processing CV fold 2
#> Processing CV fold 3
#> Processing CV fold 4
#> Processing CV fold 5
#> Processing CV fold 6
#> Processing CV fold 7
#> Processing CV fold 8
#> Processing CV fold 9
#> Processing CV fold 10After running the above code, a SummarizedExperiment object
ml_se will be returned. It includes the input abundance
data, lipid characteristic table, group information table, analysis
results, and input parameter settings. You can view the data in
ml_se by
LipidSigR::extract_summarized_experiment.
# view machine learning analysis
ml_model_result <- extract_summarized_experiment(ml_se)
# result summary
summary(ml_model_result)
#> Length Class Mode
#> abundance 229 data.frame list
#> lipid_char_table 72 data.frame list
#> group_info 2 data.frame list
#> char 2 -none- character
#> transform 1 -none- character
#> ranking_method 1 -none- character
#> ml_method 1 -none- character
#> nfold 1 -none- numeric
#> feature_option 7 -none- numeric
#> model_result 8 data.frame list
#> confusion_matrix 6 data.frame list
#> roc_result 7 data.frame list
#> pr_result 7 data.frame list
#> mean_roc_result 9 grouped_df list
#> feature_importance_result 6 data.frame list
#> selected_features 10 -none- list
#> best_model 7 -none- list
#> best_model_feature 7 -none- listml_se can also be used as input for plotting and further
analyses such as ROC/PR curve, model performance, predicted
probability, feature importance, and network analysis. Below is a brief introduction to
these functions; detailed instructions for usage will be provided in the
following sections.
“ROC/PR curve” provides overall ROC/PR curves with visualizations across CVs with different feature counts and an average ROC/PR curve for user-selected feature counts.
“Model performance” provides many valuable indicators for users to evaluate model performance. For each feature number, we calculate and plot the average value and 95% confidence interval of accuracy, sensitivity (recall), specificity, positive predictive value (precision), negative predictive value, F1 score, prevalence, detection rate, detection prevalence, and balanced accuracy in all CV runs.
“Predicted probability” displays the average predicted probabilities for each sample in the testing data across all CV runs, allowing users to explore incorrect or uncertain labels.
“Feature importance” offers tools to explore each feature’s contribution. The two methods available, ‘Algorithm-based’ and ‘SHAP analysis,’ allow for ranking and visualizing feature importance.
“Network” allows users to examine feature interactions within a machine-learning model. In this section, users can select an optimal feature count based on prior cross-validation results. The top features from the best model (based on ROC-AUC and PR-AUC) will be used to calculate correlation coefficients between them.
ROC/PR curve
Receiver Operating Characteristic (ROC) and Precision-Recall (PR) curves are commonly used to assess the diagnostic performance of binary classifiers. The mean AUC and 95% confidence interval for each feature count for both ROC and PR curves are calculated across all cross-validation (CV) runs. Generally, a higher AUC indicates better model performance. The PR curve is especially useful for datasets with a highly imbalanced class distribution (i.e., rare positive samples), providing a more informative measure of an algorithm’s effectiveness in these cases (Davis and Goadrich 2006). A random classifier typically yields an ROC-AUC around 0.5 and a PR-AUC close to the positive sample proportion. Conversely, an AUC of 1 for both metrics indicates perfect model performance.
To combine the testing results from all CV runs, 300 thresholds are evenly distributed from 0 to 1. The thresholds are then calculated for the corresponding sensitivity, specificity, precision, and recall with predicted probabilities and accurate labels of testing samples in each CV. These values are then averaged to plot a final ROC and PR curve.
Now, we are going to conduct calculation for plotting ROC curves first, and then the PR curves.
# plotting ROC curves
roc_result <- plot_ml_roc(ml_se, feature_num=10)
# result summary
summary(roc_result)
#> Length Class Mode
#> interactive_mean_auc 8 plotly list
#> static_mean_auc 9 gg list
#> initeractive_roc 8 plotly list
#> static_roc 9 gg list
#> table_mean_auc_plot 6 data.frame list
#> table_roc 5 data.frame listThe ROC curve is generated by plotting ‘sensitivity’ (the proportion of correctly classified positive samples) on the y-axis against ‘1-specificity’ (the proportion of correctly classified negative samples) on the x-axis, using various threshold values. Generally, a more robust model will have an ROC curve approaching the upper left corner
# view result: ROC curve plot
roc_result$static_mean_auc
ROC curve plot The plot shows the average ROC curve for different feature numbers with their mean AUC and 95% confidence interval.
# view result: average ROC curve plot of 10 features
roc_result$static_roc
Average ROC curve plot of 10 features The plot displays average ROC curves of user-defined features. Each CV is in grey, and the red line is the average of those cross-validations (CVs) for the ROC curves.
# plotting PR curves
pr_result <- plot_ml_pr(ml_se, feature_num=10)
# result summary
summary(pr_result)
#> Length Class Mode
#> interactive_mean_auc 8 plotly list
#> static_mean_auc 9 gg list
#> initeractive_pr 8 plotly list
#> static_pr 9 gg list
#> table_mean_auc_plot 6 data.frame list
#> table_pr 5 data.frame listThe PR curve plots ‘precision’ (the proportion of actual positives out of predicted positive samples) on the y-axis and ‘recall’ (equal to sensitivity) on the x-axis. Generally, a more robust model will have a PR curve closer to the upper right corner.
# view result: PR curve plot
pr_result$static_mean_auc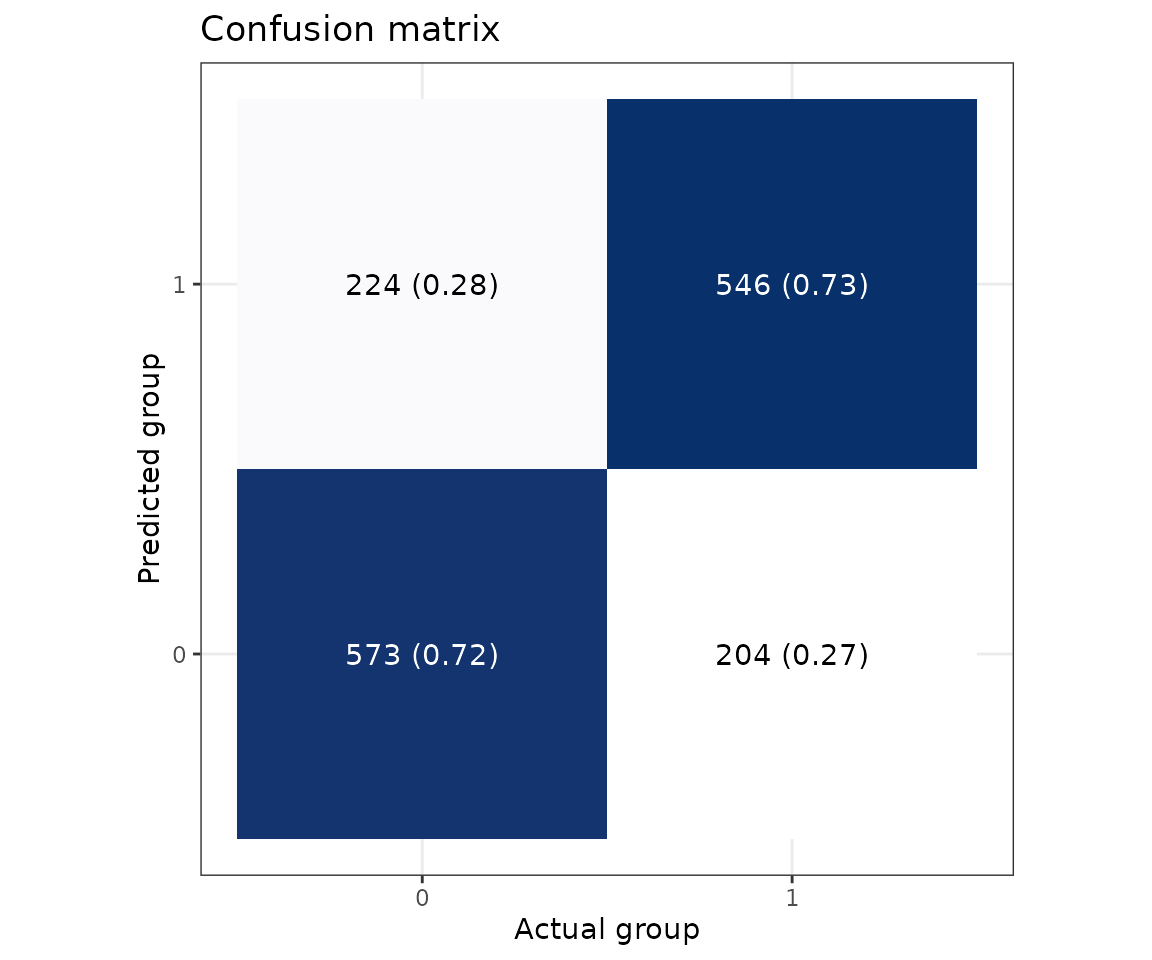
PR curve plot The plot shows the average PR curve for different feature numbers with their mean AUC and 95% confidence interval.
# view result: average PR curve plot of 10 features
pr_result$static_pr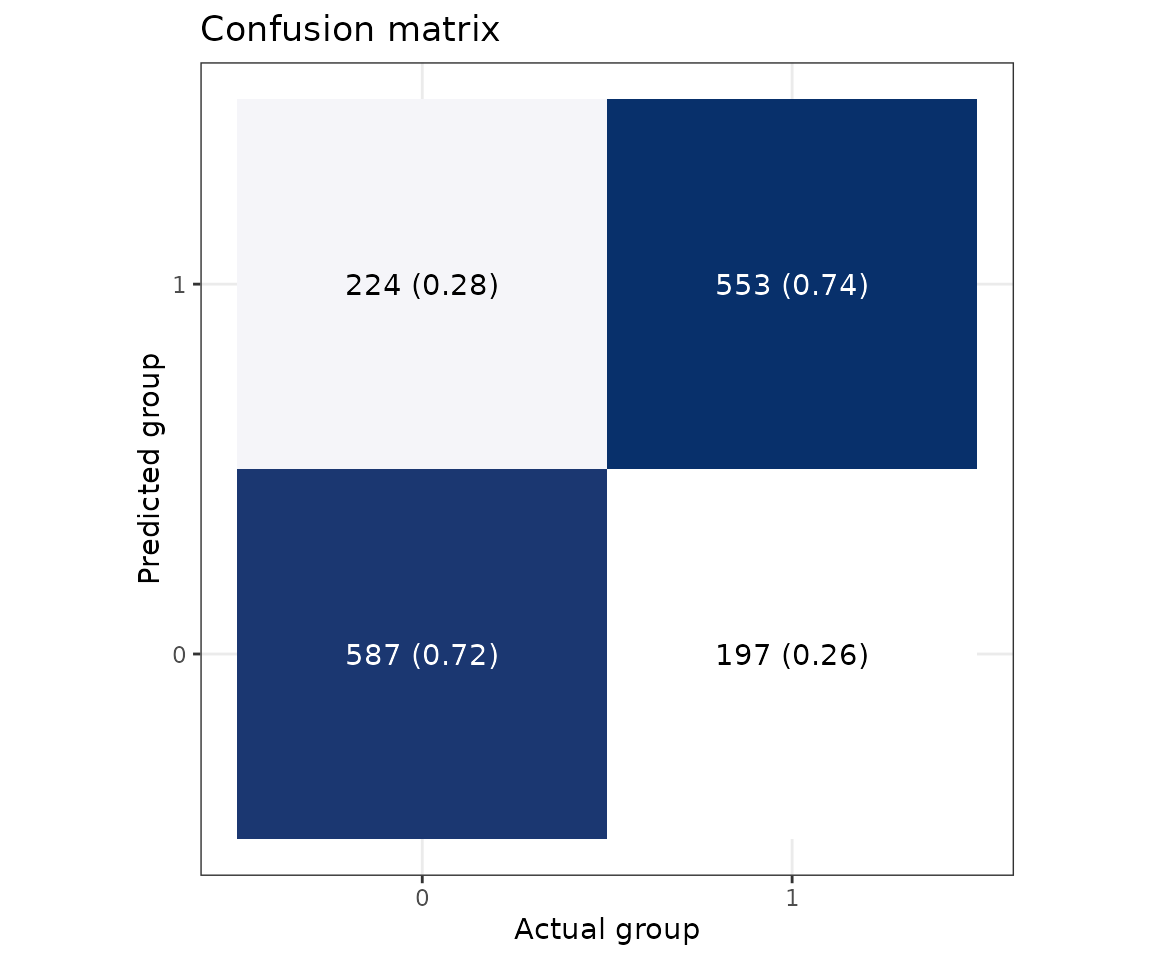
Average PR curve plot of 10 features The plot displays the average PR curves of user-defined features. Each CV is in grey, and the red line is the average of those cross-validations (CVs) for the PR curves.
Model performance
After constructing the model, it is essential to evaluate its performance. We offer several valuable indicators for this purpose. For each feature count, we calculate and plot the average value and 95% confidence interval of metrics such as accuracy, sensitivity (recall), specificity, positive predictive value (precision), negative predictive value, F1 score, prevalence, detection rate, detection prevalence, and balanced accuracy across all CV runs using the confusion matrix function in the caret package. Each of these indicators is defined in terms of true positives (TP), false positives (FP), false negatives (FN), and true negatives (TN).
Here, all the provided evaluation indicators are listed below. We can
define the evaluation method by the parameter
eval_method.
Sensitivity = Recall \(= \frac{TP}{(TP + FN)}\)
Specificity \(= \frac{TN}{(FP + TN)}\)
Prevalence \(= \frac{(TP + FN)}{(TP + FP + FN + TN)}\)
Positive predictive value (PPV) = Precision \(= \frac{TP}{(TP + FP)}\)
Negative predictive value (NPV) \(= \frac{TN}{(FN + TN)}\)
Detection rate \(= \frac{TP}{(TP + FP + FN + TN)}\)
Detection prevalence \(= \frac{(TP + FP)}{(TP + FP + FN + TN)}\)
F1 score \(= \frac{2 \times Precision \times Recall}{(Precision + Recall)}\)
# conduct model evaluation
eval_result <- plot_ml_evaluation(ml_se, eval_method='Accuracy')
# result summary
summary(eval_result)
#> Length Class Mode
#> interactive_evaluation_plot 8 plotly list
#> static_evaluation_plot 10 gg list
#> table_evaluation 7 grouped_df list
#> table_evaluation_plot 6 tbl_df list
# view result: model performance plot
eval_result$static_evaluation_plot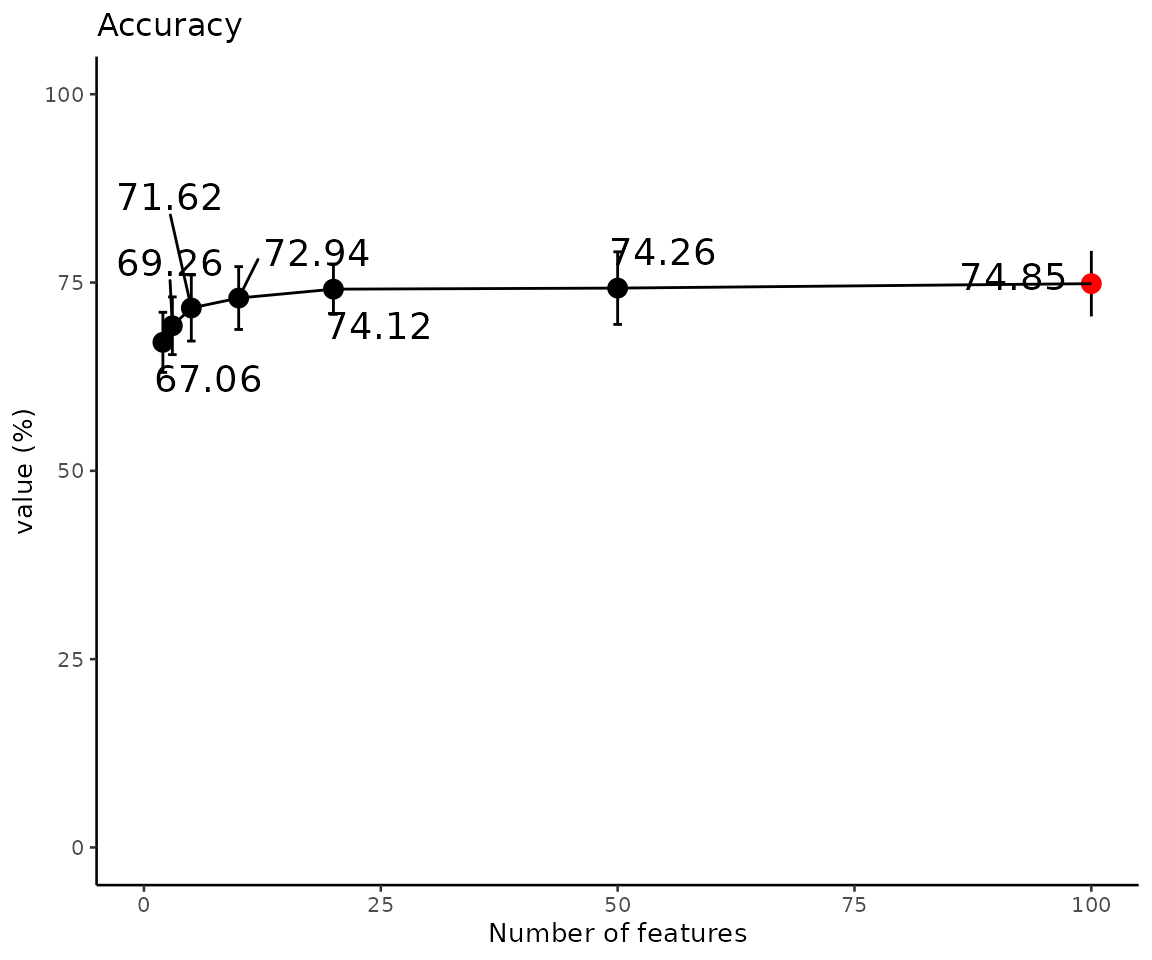
Model performance (Accuracy) The evaluation plot shows the model performance of accuracy. The highest value is marked in red.
Predicted probability
The average predicted probabilities for each sample in the testing data across all CV runs help us identify and investigate incorrect or uncertain labels.
# compute and visualize the average predicted probabilities
prob_result <- plot_ml_probability(ml_se, feature_num=10)
# result summary
summary(prob_result)
#> Length Class Mode
#> interactive_probability_plot 8 plotly list
#> static_probability_plot 10 gg list
#> static_confusion_matrix 10 gg list
#> table_probability_plot 7 data.frame list
#> table_confusion_matrix 5 grouped_df list
# view result: the distribution of predicted probabilities
prob_result$static_probability_plot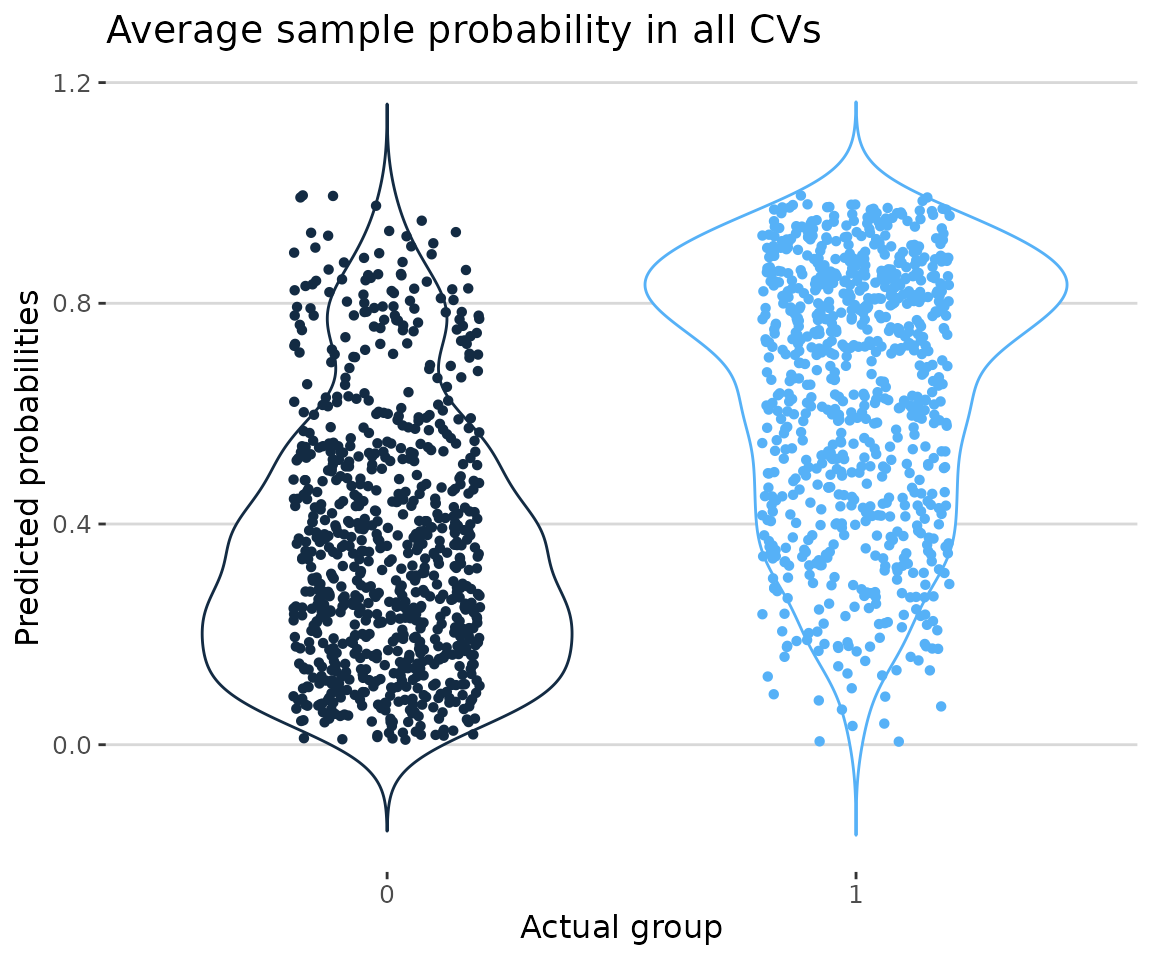
Probability plot In the plot showing the distribution of average sample probabilities across all CV runs, each point represents a sample, with its value being the mean prediction from all models in all cross-validations. The y-axis displays the predicted probabilities, indicating the likelihood that each machine learning model predicts a value of one. Specifically, the blue group represents samples where both the actual and predicted values are one, while the black group represents samples where the actual value is zero but the predicted value is one. Ideally, the black group should be as close to zero as possible, while the blue group should be as close to one.
# view result: confusion matrix of sample number and proportion
prob_result$static_confusion_matrix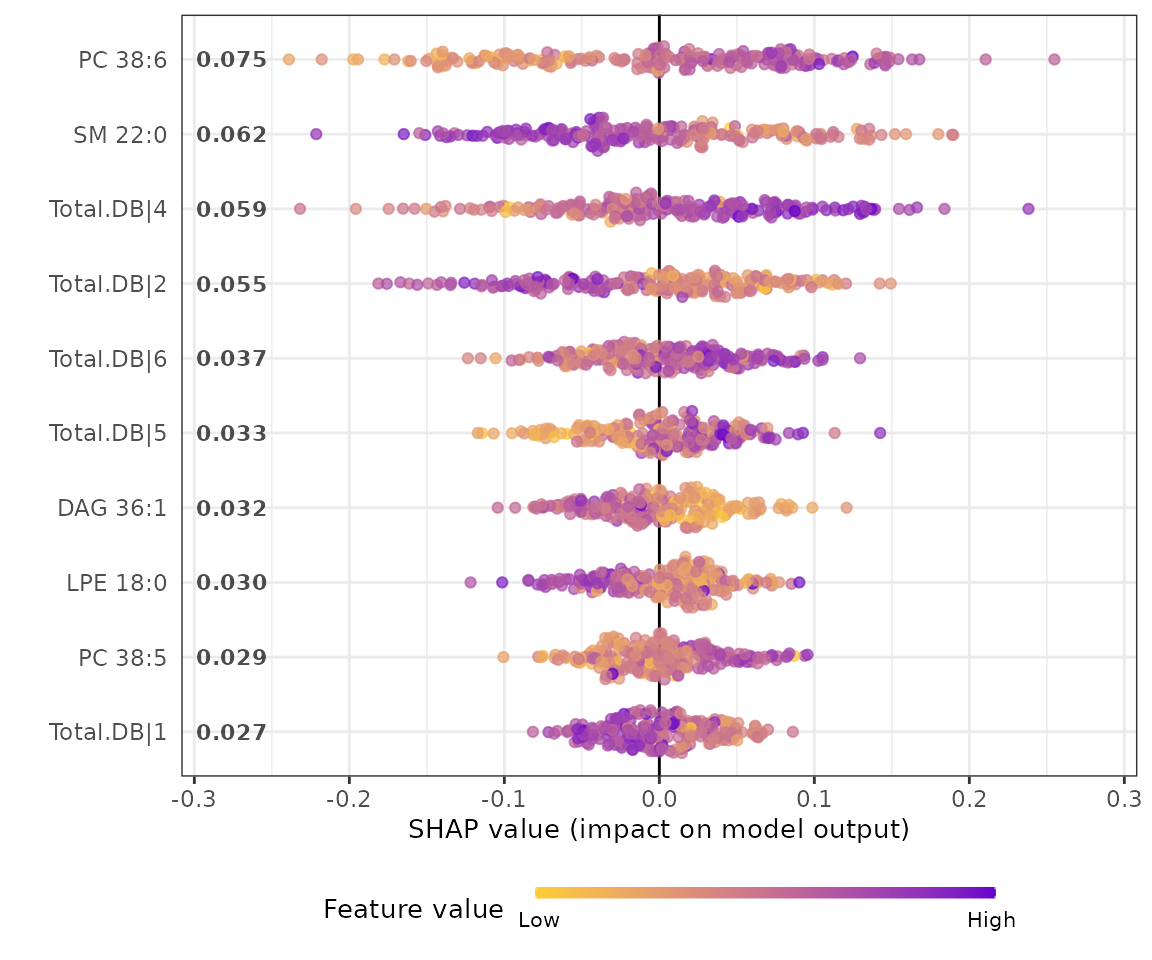
Confusion matrix In the confusion matrix, the y-axis indicates the predicted class, and the x-axis is the actual class. Therefore, the upper left is a true positive, the upper right is a false positive, the lower left is a false negative, and the lower right is a true negative. The numbers are the counts, and the number in the bracket is the percentage.
Feature importance
After building a high-accuracy model, we examine each feature’s contribution. Two methods, ‘Algorithm-based’ and ‘SHAP analysis’, are provided to rank and visualize feature importance.
Algorithm-based
In the ‘Algorithm-based’ section, setting a specific
feature count using the feature_num parameter displays the
selection frequency and average importance of the top 10 features across
all CV runs. For models like Linear SVM, Lasso, Ridge, and ElasticNet,
feature importance will be based on their coefficients’ absolute values,
and Random Forest and XGBoost use their built-in feature importance
metrics.
# compute and rank the contribution of each feature
feature_result <- plot_ml_feature(ml_se, feature_num=10)
# result summary
summary(feature_result)
#> Length Class Mode
#> interactive_selected_frequency 8 plotly list
#> static_selected_frequency 10 gg list
#> interactive_feature_importance 8 plotly list
#> static_feature_importance 10 gg list
#> table_selected_frequency 5 data.frame list
#> table_feature_importance 5 grouped_df list
# view result: selected frequency plot
feature_result$static_selected_frequency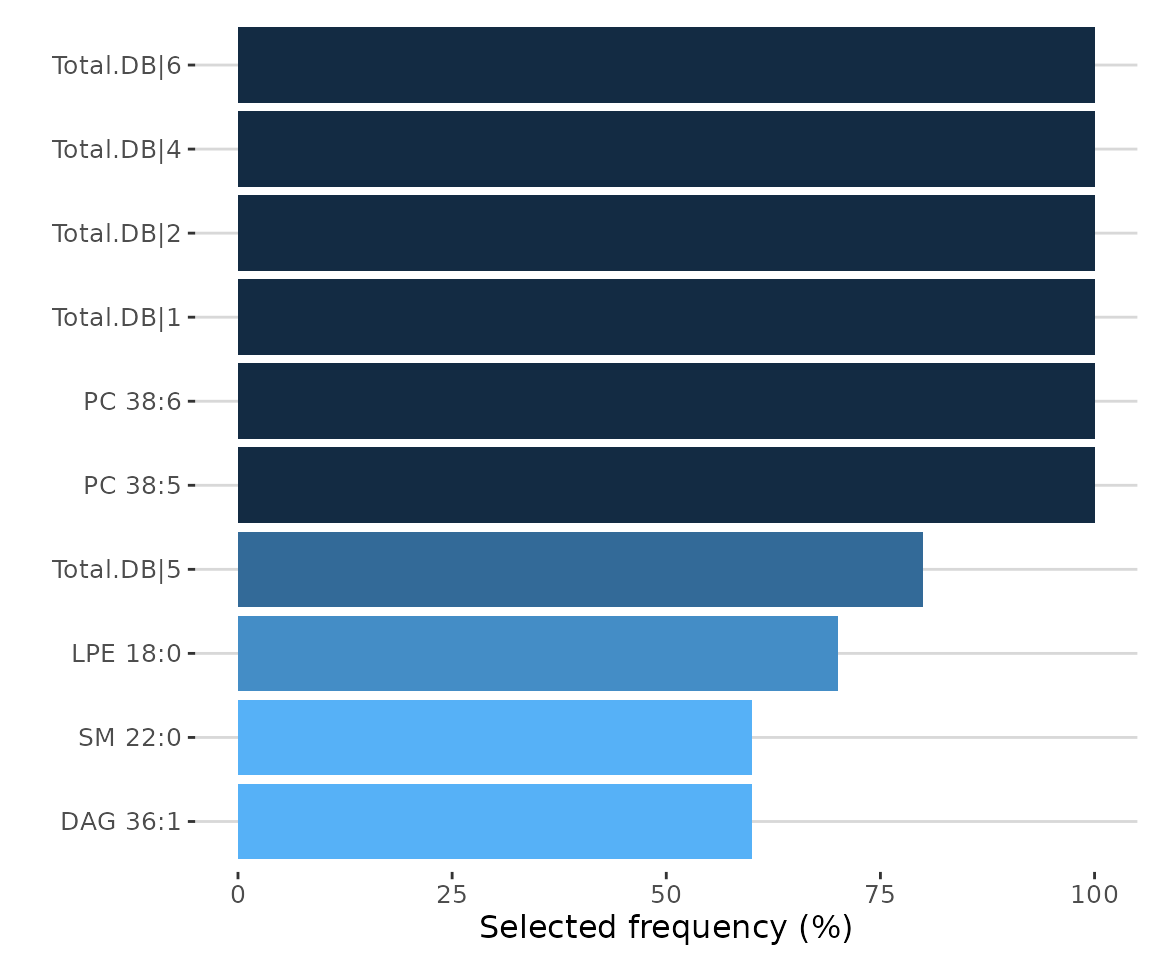
SHAP analysis
The Shapley Additive exPlanations (SHAP) method was recently introduced to explain individual predictions for any machine learning model based on Shapley values from game theory. For more detailed information, refer to the paper “A Unified Approach to Interpreting Model Predictions” (2017) (Lundberg and Lee 2017).
The analysis relies on ROC-AUC and PR-AUC results. The feature number
can be set using the feature_num parameter. Based on this
specified feature count, the best-performing model across all CVs is
selected to compute approximate Shapley values for each feature for all
samples using the fastshap package in R.
# conduct SHAP
shap_se <- ml_shap(ml_se, feature_num=10, nsim=5)
# view SHAP analysis
shap_result <- extract_summarized_experiment(shap_se)
# result summary
summary(shap_result)
#> Length Class Mode
#> abundance 11 data.frame list
#> lipid_char_table 1 data.frame list
#> feature_num 1 -none- numeric
#> nsim 1 -none- numeric
#> shap_result 6 data.frame list
#> shap_score 10 data.frame listAfter running the above code, a SummarizedExperiment object
shap_se will be returned. It includes the input abundance
data, lipid characteristic table, group information table, analysis
results, and input parameter settings. You can view the data in
shap_se by
LipidSigR::extract_summarized_experiment.
Then, you can continue to visualize the SHAP results using
LipidSigR::plot_ml_shap.
library(SHAPforxgboost)
# plot SHAP results
shap_plots <- plot_ml_shap(shap_se)
# result summary
summary(shap_plots)
#> Length Class Mode
#> interactive_feature_importance 8 plotly list
#> static_feature_importance 10 gg list
#> interactive_summary_plot 8 plotly list
#> static_summary_plot 9 gg list
#> table_feature_importance 2 data.frame list
#> table_summary_plot 10 data.table list
# view result: SHAP feature importance plot
shap_plots$static_feature_importance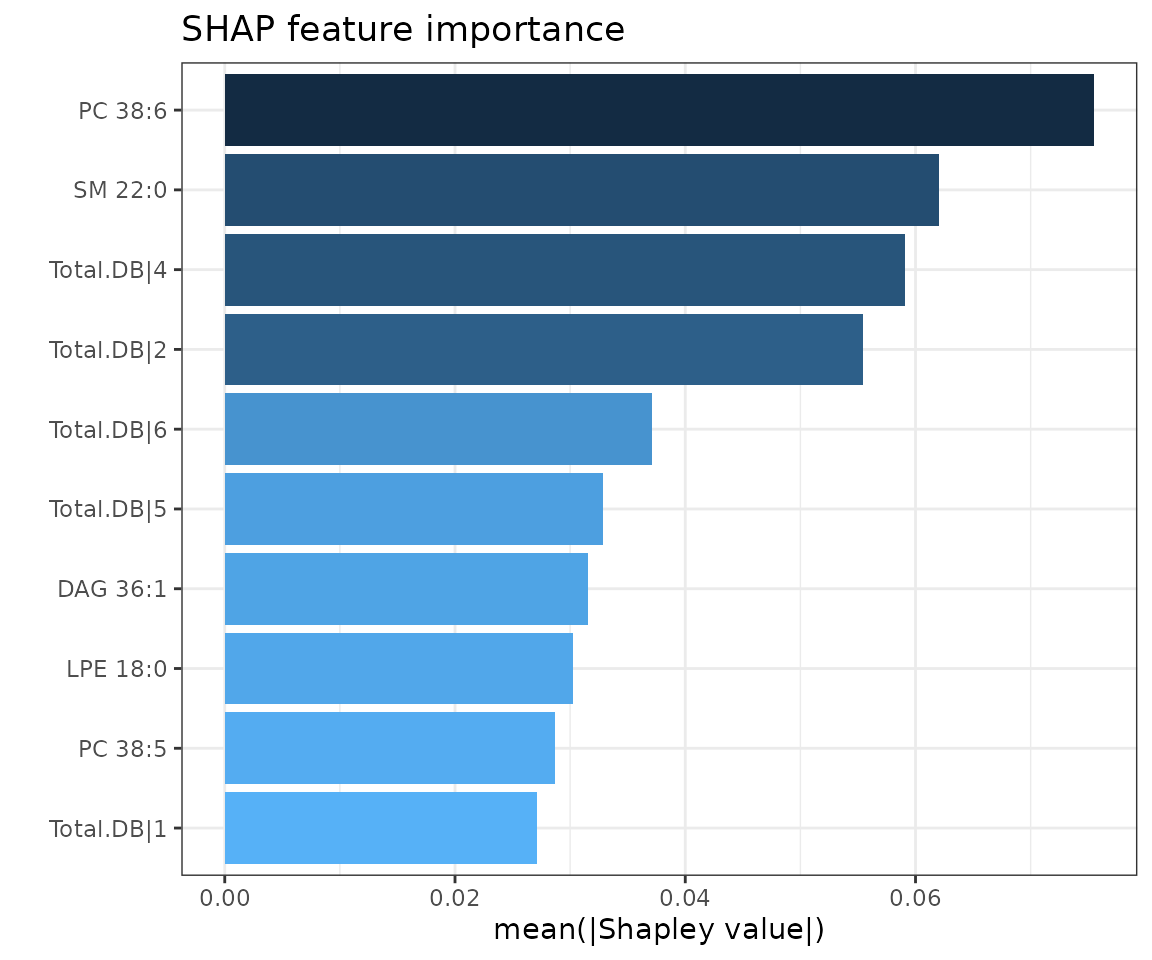
SHAP feature importance plot The top 10 features are ranked and demonstrated according to the average absolute value of shapely values from all samples.
# view result: SHAP summary plot
shap_plots$static_summary_plot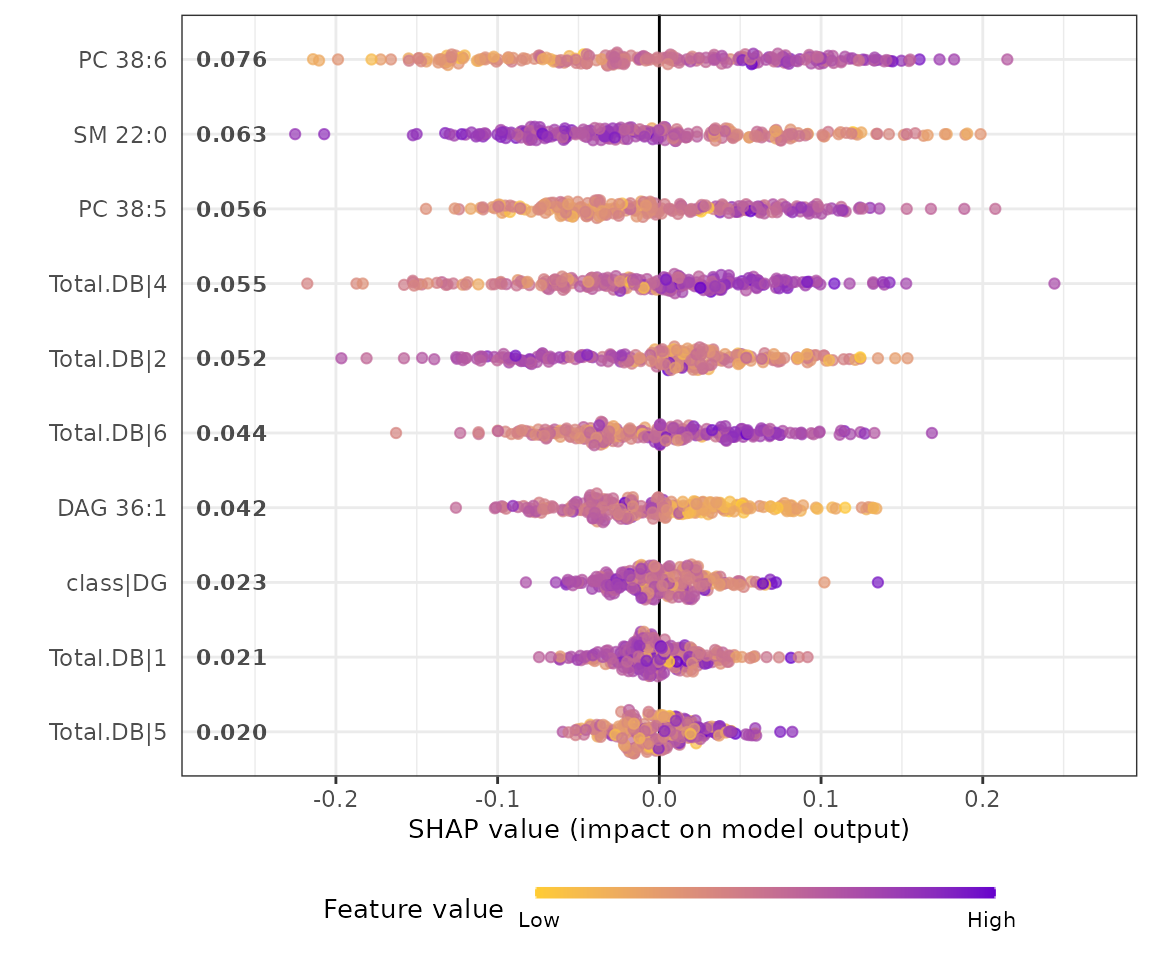
SHAP summary plot The SHAP summary plot illustrates the distribution of all shapely values for each feature. It uses Sina plot to present important features by binary patterns. The color exemplifying the value of the feature from low (yellow) to high (purple) indicates the variable is high/low for that observation. The x-axis presents whether the impact is positive or negative on quality rating (target variable). In the summary plot, the relationship between the value of a feature and the influence on the prediction is shown.
Next, we are going to visualize the SHAP feature importance of N samples.
# sample list
sample_id_list <- unique(S4Vectors::metadata(shap_se)$shap_result$ID)
# visualize SHAP feature importance of 10 samples
sample_plots <- plot_shap_sample(shap_se, sample_id=sample_id_list[10])
# result summary
summary(sample_plots)
#> Length Class Mode
#> interactive_sample_feature_importance 8 plotly list
#> static_sample_feature_importance 10 gg list
#> table_sample_feature_importance 7 data.frame list
# view result: SHAP feature importance plot of 10 samples
sample_plots$static_sample_feature_importance 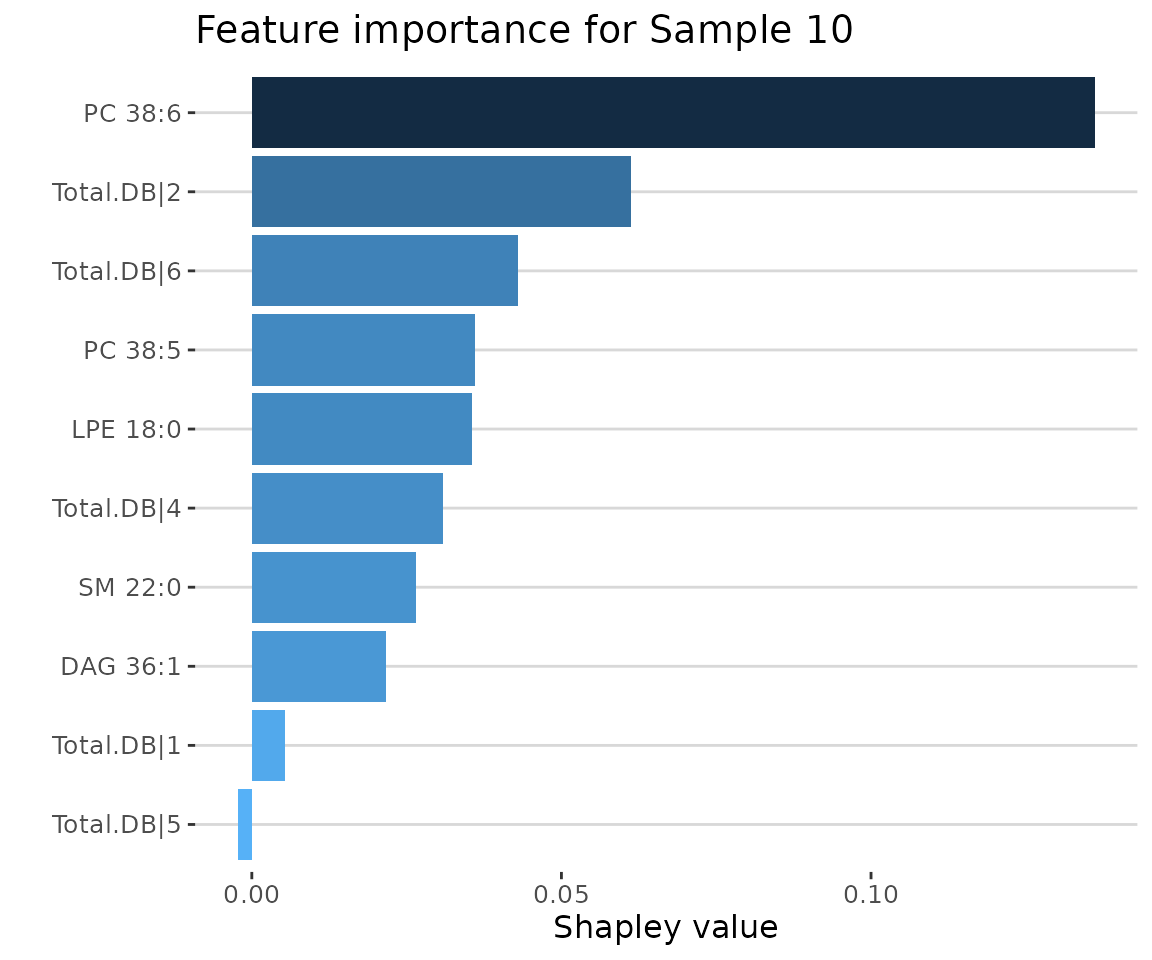
SHAP feature importance of 10 samples
Lastly, we build the SHAP force plot and dependence plot with different parameter sets.
The SHAP force plot visualizes stacked Shapley values, illustrating
how selected features impact the final output for each sample. The
top_feature parameter allows users to set the number of top
features to display, while the group_num parameter defines
the number of clusters for grouping the samples.
# visualize each predictor’s attributions
force_plots <- plot_shap_force(
shap_se, top_feature=10, cluster_method="ward.D", group_num=10)
#> All the features will be used.
# result summary
summary(force_plots)
#> Length Class Mode
#> interactive_forcePlot 8 plotly list
#> static_forcePlot 9 gg list
#> table_forcePlot 13 data.frame list
# view result: SHAP force plot
force_plots$static_forcePlot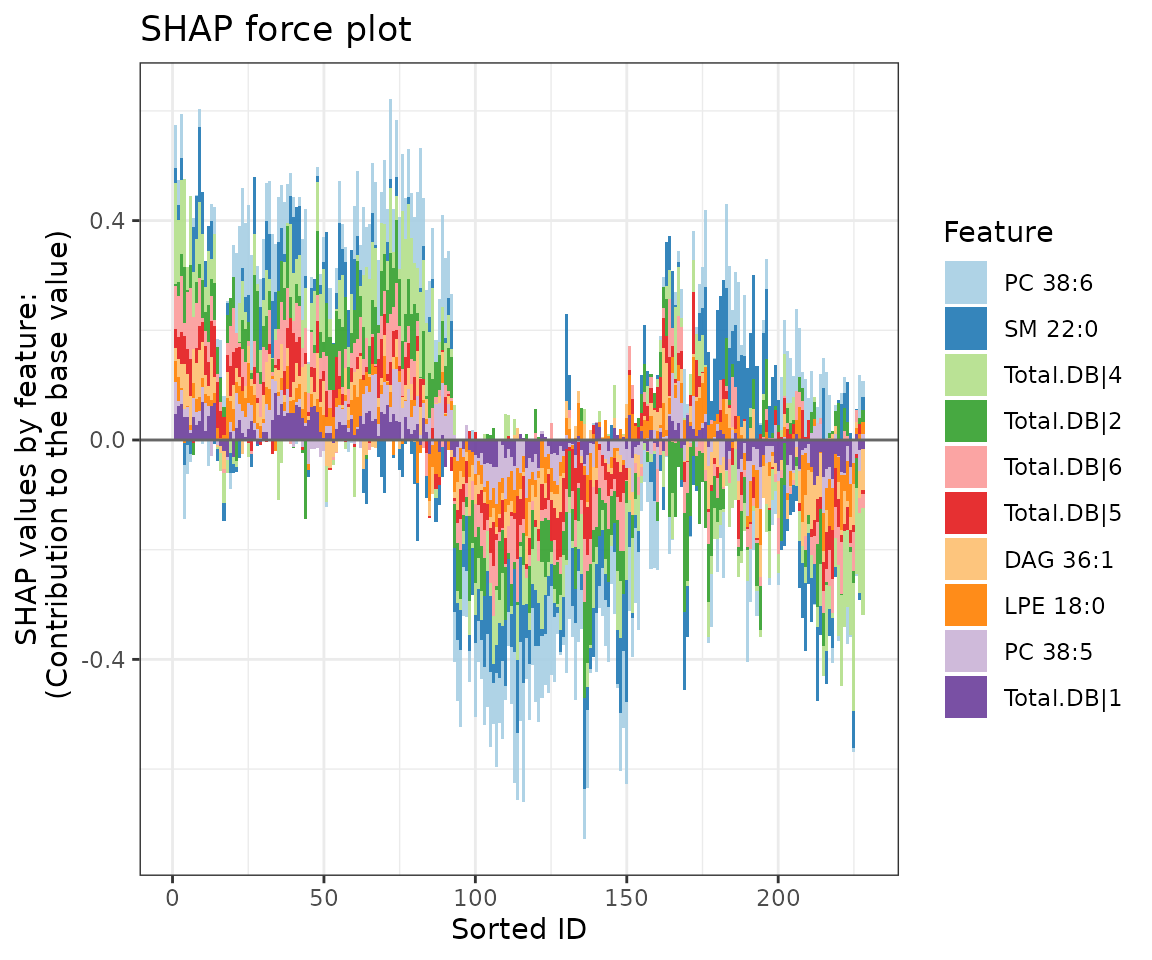
SHAP force plot The colors of the bars are filled according to the features.
The SHAP dependence plot enables exploration of how the model output varies with different feature values, revealing whether the relationship between the target variable and the feature is linear, monotonic, or more complex.
The x-axis, y-axis, and color of the plot can be customized. Typically, the x-axis represents the value of a specific feature, while the y-axis shows the corresponding Shapley value. The color parameter can be set to examine potential interaction effects between a second feature and the plotted feature.
# feature lists
selected_feature <- as.character(unique(S4Vectors::metadata(shap_se)$shap_result$variable))
# visualize SHAP values against feature values for each variable
depend_plots <- plot_shap_dependence(
shap_se, feature=selected_feature[1], shap_feature=selected_feature[2],
interaction_index=selected_feature[2])
# result summary
summary(depend_plots)
#> Length Class Mode
#> interactive_dependence_plot 8 plotly list
#> static_dependence_plot 9 gg list
#> table_dependence_plot 3 data.frame list
# view result: SHAP dependence plot
depend_plots$static_dependence_plot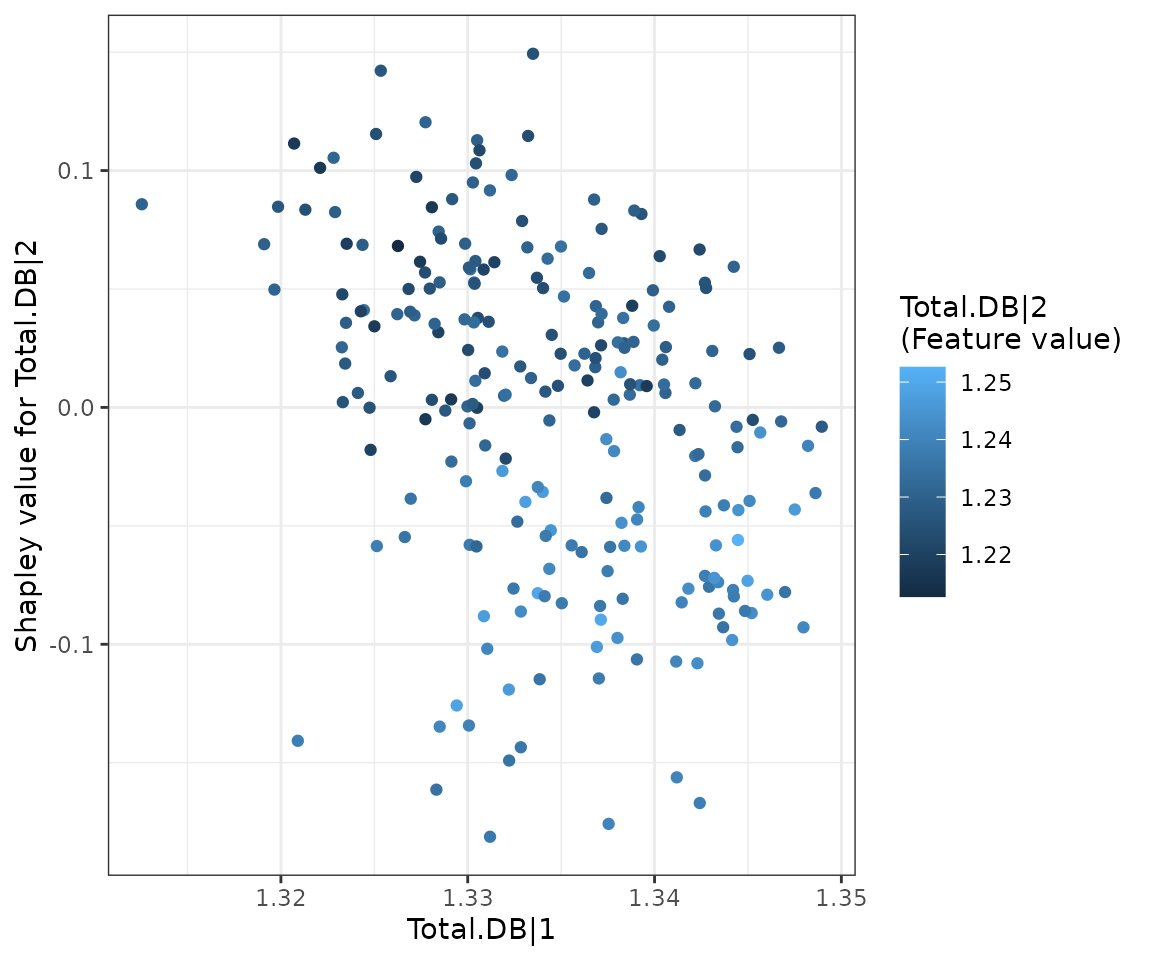
SHAP dependence plot
Network
A correlation network enables us to examine interactions between features in a machine-learning model. Based on prior cross-validation results, an optimal feature count can be selected. The features from the best-performing model (based on ROC-AUC and PR-AUC) are then used to calculate correlation coefficients between each pair of features.
Nodes (features) are shaded based on their importance in constructing the network, while line width represents the correlation coefficient value between features. Two methods, ‘Algorithm-based’ and ‘SHAP analysis,’ are available for evaluating the importance of features. Detailed information on these methods can be found in the Feature Importance section. In SHAP analysis, a positive or negative sign is assigned to feature importance based on the direction of feature values relative to the Shapley values of samples.
# compute correlation coefficients and visualize correlation network
ml_network <- ml_corr_network(
ml_se, feature_importance='Algorithm-based', correlation='pearson',
edge_cutoff=0, feature_num=10, nsim=5)
# result summary
summary(ml_network)
#> Length Class Mode
#> interactive_correlation_network 8 visNetwork list
#> static_correlation_network 10 ggraph list
#> edge_table 9 data.frame list
#> node_table 6 data.frame list
# view result: the network of feature importance
ml_network$static_correlation_network 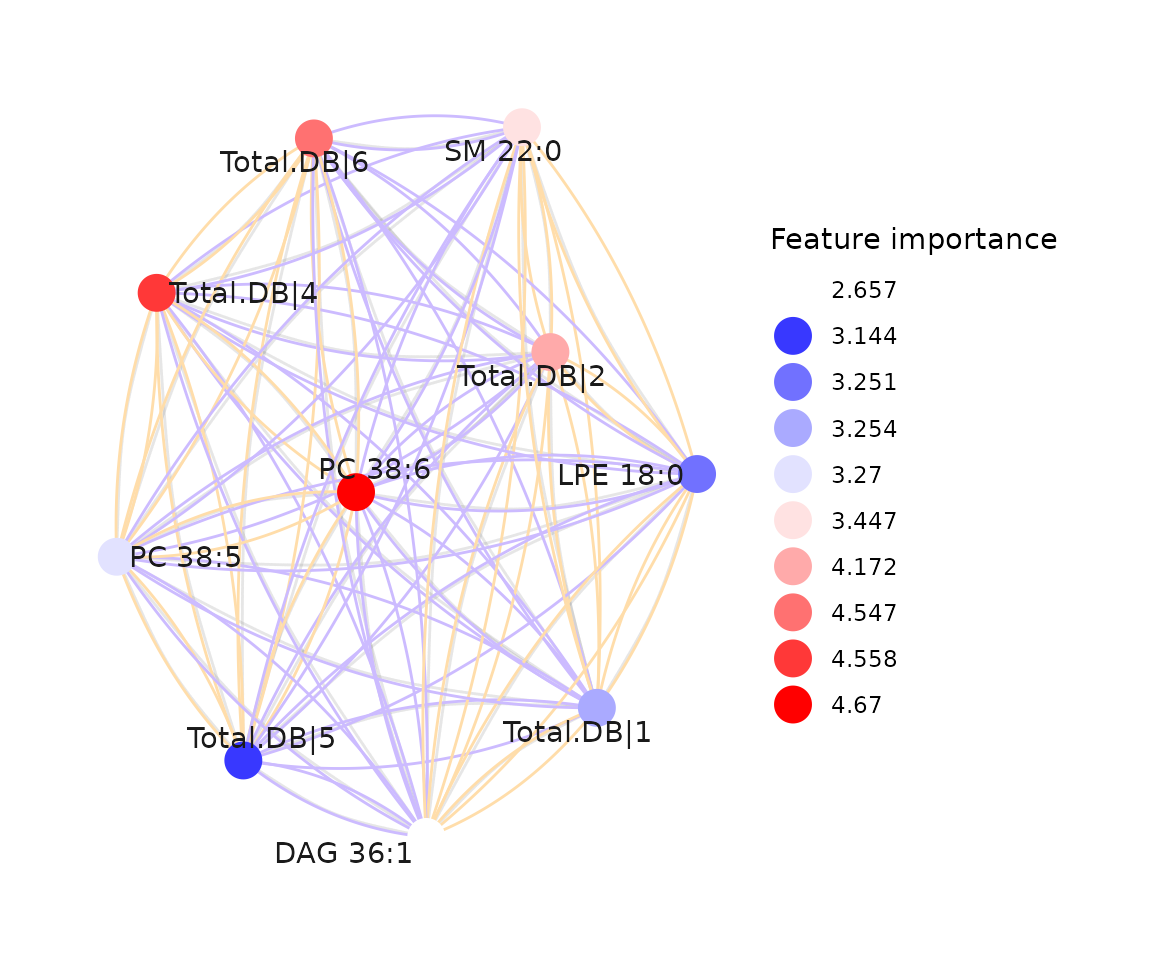
The network of feature importance
Correlation
Correlation analysis can be performed on either “lipid species” or “lipid characteristics”.
- Lipid Species Analysis: Data is analyzed at the individual lipid species level.
- Lipid Characteristics Analysis: Data is aggregated by specific lipid characteristics. The abundance of all lipid species in the same categories of a selected characteristic is summed up for analysis.
This section is designed for continuous clinical data. The
condition_col parameter specifies the column name from the
group information table that defines the clinical conditions for
analysis. Please ensure the selected columns contain only numerical data
(e.g., integers, floats). NOTE: The condition_col must include at
least two clinical conditions.
Two correlation analyses are accessible: ‘Correlation Coefficient’ and ‘Linear Regression’. Heatmaps will be shown once the correlation analysis is completed, it depicts the pattern between lipid species/lipid characteristics and clinical features.
The available clustering methods are as follows.
- Distance measurement: Pearson, Spearman, Kendall, Euclidean, Maximum, Manhattan, Canberra, Binary, and Minkowski.
- Clustering method: median, average, single, complete, Ward.D, Ward.D2, WPGMA, and UPGMC
All the analysis have to be conducted after data processing.
# data processing
processed_corr <- data_process(
corr_input, exclude_missing=TRUE, exclude_missing_pct=70,
replace_na_method='min', replace_na_method_ref=0.5,
normalization='Percentage')Correlation coefficient
The Correlation Coefficient gives a summary view of whether a
relationship exists between clinical features and lipid species, how
strong that relationship is, and whether the relationship is positive or
negative. The parameters’ cor_coef_cutoff and
p_cutoff can decide the correlation coefficient and p-value
cut-offs. The rule of thumb in medical research recommended by Mukaka
for interpreting the size of a correlation coefficient is provided below
(Mukaka 2012).
| Size of Correlation | Interpretation |
|---|---|
| 0.90 to 1.00 (-.90 to -1.00) | Very high positive (negative) correlation |
| 0.70 to .90 (-.70 to -.90) | High positive (negative) correlation |
| 0.50 to .70 (-.50 to -.70) | Moderate positive (negative) correlation |
| 0.30 to .50 (-.30 to -.50) | Low positive (negative) correlation |
| 0.00 to .30 (.00 to -.30) | negligible correlation |
First, we will conduct a correlation analysis for lipid species. Set
the type parameter to Sp. You can optionally
visualize the heatmap with side colors. To do this, specify the desired
characteristic in the side_color_char parameter. Here, we
use class as an example. If you prefer not to display side
colors, set side_color_char to NULL. NOTE: The
char parameter must be set to NULL for lipid species
correlation.
Before the analysis, we must determine the condition_col
parameter, selected from the column names from the group information
table. Follow the steps below to view all available options for
condition_col.
# extract group information table
group_info <- extract_summarized_experiment(processed_corr)$group_info
# condition_col options (choose only columns with numeric values)
condition_col_option <- str(group_info[-1])
#> 'data.frame': 129 obs. of 8 variables:
#> $ FEV1_FVC : num 0.29 0.57 0.79 0.39 0.37 0.41 0.79 0.58 0.39 0.48 ...
#> $ Emphysema : num 11.017 2.361 0.983 34.993 26.85 ...
#> $ Exacerbations: num 6 0 0 0 0 0 5 0 0 0 ...
#> $ Age : num 48.7 70.1 49.6 54.1 70.5 58.8 71.5 69.5 72.2 69.3 ...
#> $ Sex : num 0 0 0 1 0 1 0 0 1 1 ...
#> $ Smoking : num 0 0 0 0 0 0 0 0 1 0 ...
#> $ BMI : num 36.5 27.9 23.9 28.4 23.2 ...
#> $ FEV1 : num 14.9 66.7 99.9 31.2 31.6 57.7 98.1 54.3 44.4 46.3 ...
# list the available lipid characteristics for `side_color_char`
list_lipid_char(processed_corr)$common_list
#> Lipid classification Lipid classification
#> "Category" "Main.Class"
#> Lipid classification Lipid classification
#> "Sub.Class" "class"
#> Fatty acid properties Fatty acid properties
#> "FA" "FA.C"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category1" "FA.Chain.Length.Category2"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category3" "FA.DB"
#> Fatty acid properties Fatty acid properties
#> "FA.OH" "FA.Unsaturation.Category1"
#> Fatty acid properties Fatty acid properties
#> "FA.Unsaturation.Category2" "Total.C"
#> Fatty acid properties Fatty acid properties
#> "Total.DB" "Total.FA"
#> Fatty acid properties Physical or chemical properties
#> "Total.OH" "Headgroup.Charge"
#> Physical or chemical properties Physical or chemical properties
#> "Intrinsic.Curvature" "Transition.Temperature"
#> Cellular component Function
#> "Cellular.Component" "Function"
# compute correlation coefficient and visualize by heatmap
res_sp <- corr_cor_heatmap(
processed_corr, char=NULL,
condition_col=c("FEV1_FVC", "Emphysema", "Exacerbations"),
side_color_char='class', correlation='pearson', significant='pval',
p_cutoff=1, adjust_p_method='BH', cor_coef_cutoff=0,
distfun='spearman', hclustfun='average', heatmap_col='statistic',
transform='log10', type='Sp')
#> Registered S3 methods overwritten by 'registry':
#> method from
#> print.registry_field proxy
#> print.registry_entry proxy
# result summary
summary(res_sp)
#> Length Class Mode
#> all_correlation_result 9 data.frame list
#> sig_correlation_result 9 data.frame list
#> interactive_heatmap 8 plotly list
#> static_heatmap 3 recordedplot list
#> heatmap_matrix 150 -none- numeric
# view result: heatmap of clinical features and lipid species
res_sp$static_heatmap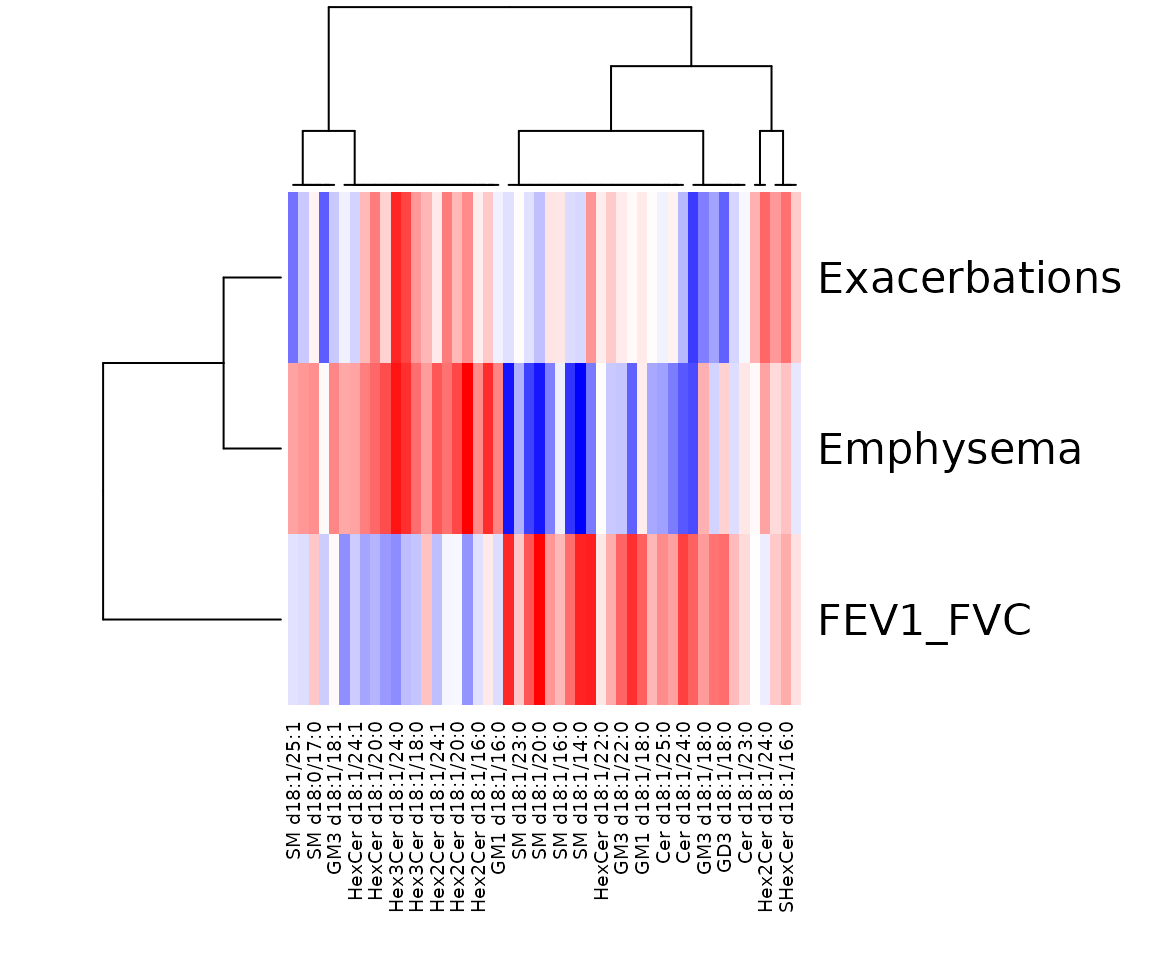
Correlation coefficient for lipid species analysis The heatmap shows only the variables that pass the defined cut-offs for the p-value and the correlation coefficient. The rows are clinical features, and the columns are the lipid species.
Next, we move on to conduct a correlation analysis of lipid
characteristics. Set the type parameter to
Char and specify a lipid characteristic for the
char parameter. You can use
LipidSigR::list_lipid_char to view a list of available
lipid characteristics. For more detailed information, please refer to
vignette("1_tool_function").
NOTE: The side_color_char parameter must be set to
NULL for lipid characteristics correlation.
# list the available lipid characteristics for `char`
list_lipid_char(processed_corr)$common_list
#> Lipid classification Lipid classification
#> "Category" "Main.Class"
#> Lipid classification Lipid classification
#> "Sub.Class" "class"
#> Fatty acid properties Fatty acid properties
#> "FA" "FA.C"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category1" "FA.Chain.Length.Category2"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category3" "FA.DB"
#> Fatty acid properties Fatty acid properties
#> "FA.OH" "FA.Unsaturation.Category1"
#> Fatty acid properties Fatty acid properties
#> "FA.Unsaturation.Category2" "Total.C"
#> Fatty acid properties Fatty acid properties
#> "Total.DB" "Total.FA"
#> Fatty acid properties Physical or chemical properties
#> "Total.OH" "Headgroup.Charge"
#> Physical or chemical properties Physical or chemical properties
#> "Intrinsic.Curvature" "Transition.Temperature"
#> Cellular component Function
#> "Cellular.Component" "Function"
# compute correlation coefficient and visualize by heatmap
res_char <- corr_cor_heatmap(
processed_corr, char="class",
condition_col=c("FEV1_FVC", "Emphysema", "Exacerbations"),
side_color_char=NULL, correlation='pearson', significant='pval',
p_cutoff=1, adjust_p_method='BH', cor_coef_cutoff=0,
distfun='spearman', hclustfun='average', heatmap_col='statistic',
transform='log10', type='Char')
# result summary
summary(res_char)
#> Length Class Mode
#> all_correlation_result 9 data.frame list
#> sig_correlation_result 9 data.frame list
#> interactive_heatmap 8 plotly list
#> static_heatmap 3 recordedplot list
#> heatmap_matrix 30 -none- numeric
# view result: heatmap of clinical features and lipid characteristics
res_char$static_heatmap
Correlation coefficient for lipid characteristics analysis The heatmap shows only the variables that pass the defined cut-offs for the p-value and the correlation coefficient. The rows are clinical features, and the columns are lipid characteristics.
Linear regression
Linear regression is a statistical method used to model the relationship between a dependent variable (e.g., lipid level) and one or more independent variables (e.g., clinical features). By analyzing these relationships, we can estimate the impact of specific clinical factors on lipid levels.
In multiple linear regression, we incorporate additional variables to
account for potential confounding factors. To do this, we specify the
adjusted_col parameter, which refers to the column names
selected from the group information table. Once the analysis is
complete, each lipid species is assigned a beta coefficient and a
corresponding t-statistic (p-value). These values can be used to
identify significant associations and group similar lipid species for
further analysis.
First, we will conduct a correlation analysis for lipid species. Set
the type parameter to Sp. You can optionally
visualize the heatmap with side colors. To do this, specify the desired
characteristic in the side_color_char parameter. Here, we
use class as an example. If you prefer not to display side
colors, set side_color_char to NULL.
NOTE: The char parameter must be set to NULL for
lipid species correlation.
Before the analysis, we must determine the condition_col
and adjusted_col parameters, selected from the column names
from the group information table. Follow the steps below to view all
available options for condition_col and
adjusted_col.
# extract group information table
group_info <- extract_summarized_experiment(processed_corr)$group_info
# condition_col options (choose only columns with numeric values)
condition_col_option <- str(group_info[-1])
#> 'data.frame': 129 obs. of 8 variables:
#> $ FEV1_FVC : num 0.29 0.57 0.79 0.39 0.37 0.41 0.79 0.58 0.39 0.48 ...
#> $ Emphysema : num 11.017 2.361 0.983 34.993 26.85 ...
#> $ Exacerbations: num 6 0 0 0 0 0 5 0 0 0 ...
#> $ Age : num 48.7 70.1 49.6 54.1 70.5 58.8 71.5 69.5 72.2 69.3 ...
#> $ Sex : num 0 0 0 1 0 1 0 0 1 1 ...
#> $ Smoking : num 0 0 0 0 0 0 0 0 1 0 ...
#> $ BMI : num 36.5 27.9 23.9 28.4 23.2 ...
#> $ FEV1 : num 14.9 66.7 99.9 31.2 31.6 57.7 98.1 54.3 44.4 46.3 ...
# adjusted_col options
adjusted_col_option <- str(group_info[-1])
#> 'data.frame': 129 obs. of 8 variables:
#> $ FEV1_FVC : num 0.29 0.57 0.79 0.39 0.37 0.41 0.79 0.58 0.39 0.48 ...
#> $ Emphysema : num 11.017 2.361 0.983 34.993 26.85 ...
#> $ Exacerbations: num 6 0 0 0 0 0 5 0 0 0 ...
#> $ Age : num 48.7 70.1 49.6 54.1 70.5 58.8 71.5 69.5 72.2 69.3 ...
#> $ Sex : num 0 0 0 1 0 1 0 0 1 1 ...
#> $ Smoking : num 0 0 0 0 0 0 0 0 1 0 ...
#> $ BMI : num 36.5 27.9 23.9 28.4 23.2 ...
#> $ FEV1 : num 14.9 66.7 99.9 31.2 31.6 57.7 98.1 54.3 44.4 46.3 ...
# list the available lipid characteristics for `side_color_char`
list_lipid_char(processed_corr)$common_list
#> Lipid classification Lipid classification
#> "Category" "Main.Class"
#> Lipid classification Lipid classification
#> "Sub.Class" "class"
#> Fatty acid properties Fatty acid properties
#> "FA" "FA.C"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category1" "FA.Chain.Length.Category2"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category3" "FA.DB"
#> Fatty acid properties Fatty acid properties
#> "FA.OH" "FA.Unsaturation.Category1"
#> Fatty acid properties Fatty acid properties
#> "FA.Unsaturation.Category2" "Total.C"
#> Fatty acid properties Fatty acid properties
#> "Total.DB" "Total.FA"
#> Fatty acid properties Physical or chemical properties
#> "Total.OH" "Headgroup.Charge"
#> Physical or chemical properties Physical or chemical properties
#> "Intrinsic.Curvature" "Transition.Temperature"
#> Cellular component Function
#> "Cellular.Component" "Function"
# compute linear regression and visualize by heatmap
res_sp <- corr_lr_heatmap(
processed_corr, char=NULL,
condition_col=c("FEV1_FVC", "Emphysema", "Exacerbations"),
adjusted_col=c("Age", "Sex", "Smoking", "BMI", "FEV1"),
side_color_char=NULL, significant='pval', p_cutoff=0.05,
adjust_p_method='BH', distfun='spearman', hclustfun='centroid',
heatmap_col='t_statistic', transform='log10', type='Sp')
# result summary
summary(res_sp)
#> Length Class Mode
#> all_correlation_result 9 data.frame list
#> sig_correlation_result 9 data.frame list
#> interactive_heatmap 8 plotly list
#> static_heatmap 3 recordedplot list
#> heatmap_matrix 14 -none- numeric
# view result: heatmap of linear regression
res_sp$static_heatmap
The heatmap of linear regression for lipid species analysis The heatmap shows only the variables that pass the user-defined cut-offs for p-value and correlation coefficient. The rows are clinical features, and the columns are lipid species.
Next, we move on to conduct a correlation analysis of lipid
characteristics. Set the type parameter to
Char and specify a lipid characteristic for the
char parameter. You can use
LipidSigR::list_lipid_char to view a list of available
lipid characteristics. For more detailed information, please refer to
vignette("1_tool_function").
NOTE: The side_color_char parameter must be set to
NULL for lipid characteristics correlation.
# list the available lipid characteristics for `char`
list_lipid_char(processed_corr)$common_list
#> Lipid classification Lipid classification
#> "Category" "Main.Class"
#> Lipid classification Lipid classification
#> "Sub.Class" "class"
#> Fatty acid properties Fatty acid properties
#> "FA" "FA.C"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category1" "FA.Chain.Length.Category2"
#> Fatty acid properties Fatty acid properties
#> "FA.Chain.Length.Category3" "FA.DB"
#> Fatty acid properties Fatty acid properties
#> "FA.OH" "FA.Unsaturation.Category1"
#> Fatty acid properties Fatty acid properties
#> "FA.Unsaturation.Category2" "Total.C"
#> Fatty acid properties Fatty acid properties
#> "Total.DB" "Total.FA"
#> Fatty acid properties Physical or chemical properties
#> "Total.OH" "Headgroup.Charge"
#> Physical or chemical properties Physical or chemical properties
#> "Intrinsic.Curvature" "Transition.Temperature"
#> Cellular component Function
#> "Cellular.Component" "Function"
# compute linear regression and visualize by heatmap
res_char <- corr_lr_heatmap(
processed_corr, char="class",
condition_col=c("FEV1_FVC", "Emphysema", "Exacerbations"),
adjusted_col=c("Age", "Sex", "Smoking", "BMI", "FEV1"),
side_color_char=NULL, significant='pval', p_cutoff=1,
adjust_p_method='BH', distfun='spearman', hclustfun='centroid',
heatmap_col='t_statistic', transform='log10', type='Char')
# result summary
summary(res_char)
#> Length Class Mode
#> all_correlation_result 9 data.frame list
#> sig_correlation_result 9 data.frame list
#> interactive_heatmap 8 plotly list
#> static_heatmap 3 recordedplot list
#> heatmap_matrix 30 -none- numeric
# view result: heatmap of linear regression
res_char$static_heatmap
The heatmap of linear regression for lipid characteristics analysis Only the variables that pass the user-defined cut-offs for p-value and correlation coefficient are shown on the heatmap. The rows of the heatmap are clinical features, and the columns are lipid characteristics.
Session info
#> R version 4.2.3 (2023-03-15)
#> Platform: x86_64-pc-linux-gnu (64-bit)
#> Running under: CentOS Stream 8
#>
#> Matrix products: default
#> BLAS/LAPACK: /usr/lib64/libopenblasp-r0.3.15.so
#>
#> locale:
#> [1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
#> [3] LC_TIME=en_US.UTF-8 LC_COLLATE=en_US.UTF-8
#> [5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
#> [7] LC_PAPER=en_US.UTF-8 LC_NAME=C
#> [9] LC_ADDRESS=C LC_TELEPHONE=C
#> [11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] visNetwork_2.1.2 LipidSigR_1.0.0 SHAPforxgboost_0.1.3
#> [4] dplyr_1.1.3
#>
#> loaded via a namespace (and not attached):
#> [1] utf8_1.2.3 tidyselect_1.2.0
#> [3] heatmaply_1.4.2 RSQLite_2.3.5
#> [5] AnnotationDbi_1.60.2 htmlwidgets_1.6.2
#> [7] TSP_1.2-4 grid_4.2.3
#> [9] ranger_0.15.1 BiocParallel_1.32.6
#> [11] Rtsne_0.16 pROC_1.18.4
#> [13] munsell_0.5.0 codetools_0.2-19
#> [15] ragg_1.3.0 xgboost_1.7.5.1
#> [17] future_1.33.0 withr_3.0.0
#> [19] colorspace_2.1-0 Biobase_2.58.0
#> [21] knitr_1.44 rstudioapi_0.15.0
#> [23] stats4_4.2.3 rgoslin_1.2.0
#> [25] ggsignif_0.6.4 ca_0.71.1
#> [27] listenv_0.9.0 MatrixGenerics_1.10.0
#> [29] labeling_0.4.3 GenomeInfoDbData_1.2.9
#> [31] polyclip_1.10-4 bit64_4.0.5
#> [33] farver_2.1.1 rprojroot_2.0.3
#> [35] parallelly_1.36.0 vctrs_0.6.3
#> [37] generics_0.1.3 ipred_0.9-14
#> [39] xfun_0.42 timechange_0.2.0
#> [41] ggthemes_4.2.4 fastcluster_1.2.3
#> [43] R6_2.5.1 GenomeInfoDb_1.34.9
#> [45] graphlayouts_1.0.1 seriation_1.5.1
#> [47] bitops_1.0-7 cachem_1.0.8
#> [49] reshape_0.8.9 fgsea_1.24.0
#> [51] DelayedArray_0.24.0 assertthat_0.2.1
#> [53] scales_1.3.0 ggraph_2.1.0
#> [55] nnet_7.3-19 gtable_0.3.4
#> [57] fastshap_0.1.0 globals_0.16.2
#> [59] tidygraph_1.2.3 timeDate_4022.108
#> [61] rlang_1.1.1 BBmisc_1.13
#> [63] systemfonts_1.0.4 splines_4.2.3
#> [65] rstatix_0.7.2 lazyeval_0.2.2
#> [67] yardstick_1.2.0 ModelMetrics_1.2.2.2
#> [69] wordcloud_2.6 broom_1.0.5
#> [71] checkmate_2.2.0 yaml_2.3.7
#> [73] reshape2_1.4.4 abind_1.4-5
#> [75] crosstalk_1.2.0 backports_1.4.1
#> [77] Hmisc_5.1-1 mwcsr_0.1.7
#> [79] caret_6.0-94 lava_1.7.2.1
#> [81] tools_4.2.3 ggplot2_3.4.3
#> [83] ellipsis_0.3.2 jquerylib_0.1.4
#> [85] RColorBrewer_1.1-3 proxy_0.4-27
#> [87] BiocGenerics_0.44.0 Rcpp_1.0.11
#> [89] plyr_1.8.8 base64enc_0.1-3
#> [91] zlibbioc_1.44.0 purrr_1.0.2
#> [93] RCurl_1.98-1.12 ggpubr_0.6.0
#> [95] rpart_4.1.19 viridis_0.6.4
#> [97] cowplot_1.1.1 S4Vectors_0.36.2
#> [99] SummarizedExperiment_1.28.0 ggrepel_0.9.3
#> [101] cluster_2.1.4 fs_1.6.3
#> [103] factoextra_1.0.7 furrr_0.3.1
#> [105] magrittr_2.0.3 data.table_1.15.2
#> [107] RSpectra_0.16-1 hwordcloud_0.1.0
#> [109] matrixStats_1.0.0 evaluate_0.21
#> [111] XML_3.99-0.14 gatom_0.99.3
#> [113] IRanges_2.32.0 gridExtra_2.3
#> [115] compiler_4.2.3 ellipse_0.5.0
#> [117] tibble_3.2.1 crayon_1.5.2
#> [119] htmltools_0.5.6 corpcor_1.6.10
#> [121] Formula_1.2-5 tidyr_1.3.0
#> [123] lubridate_1.9.2 DBI_1.2.2
#> [125] tweenr_2.0.3 MASS_7.3-60
#> [127] Matrix_1.6-3 car_3.1-2
#> [129] cli_3.6.1 pryr_0.1.6
#> [131] parallel_4.2.3 gower_1.0.1
#> [133] igraph_1.5.1 GenomicRanges_1.50.2
#> [135] pkgconfig_2.0.3 pkgdown_2.0.7
#> [137] registry_0.5-1 foreign_0.8-85
#> [139] plotly_4.10.4 recipes_1.0.8
#> [141] foreach_1.5.2 rARPACK_0.11-0
#> [143] hardhat_1.3.0 bslib_0.5.1
#> [145] webshot_0.5.5 XVector_0.38.0
#> [147] prodlim_2023.08.28 iheatmapr_0.7.0
#> [149] BioNet_1.58.0 stringr_1.5.0
#> [151] digest_0.6.33 Biostrings_2.66.0
#> [153] rmarkdown_2.25 fastmatch_1.1-4
#> [155] htmlTable_2.4.1 dendextend_1.17.1
#> [157] uwot_0.1.16 lifecycle_1.0.3
#> [159] nlme_3.1-163 jsonlite_1.8.7
#> [161] carData_3.0-5 mixOmics_6.22.0
#> [163] desc_1.4.2 viridisLite_0.4.2
#> [165] shinyCyJS_1.0.0 fansi_1.0.4
#> [167] pillar_1.9.0 lattice_0.22-5
#> [169] GGally_2.1.2 survival_3.5-7
#> [171] KEGGREST_1.38.0 fastmap_1.1.1
#> [173] httr_1.4.7 glue_1.6.2
#> [175] FNN_1.1.3.2 png_0.1-8
#> [177] iterators_1.0.14 bit_4.0.5
#> [179] class_7.3-22 ggforce_0.4.1
#> [181] stringi_1.7.12 sass_0.4.7
#> [183] blob_1.2.4 textshaping_0.3.6
#> [185] rsample_1.2.0 memoise_2.0.1
#> [187] e1071_1.7-13 future.apply_1.11.0
#> [189] irlba_2.3.5.1