LipidSig 2.0: Integrating Lipid Characteristic Insights into Advanced Lipidomics Data Analysis
FAQ 1: What is LipidSig? What is different from LipidSigv1 to v2?
-
LipidSig is the first web-based platform which integrates a comprehensive analysis for streamlined data mining of lipidomic datasets.
-
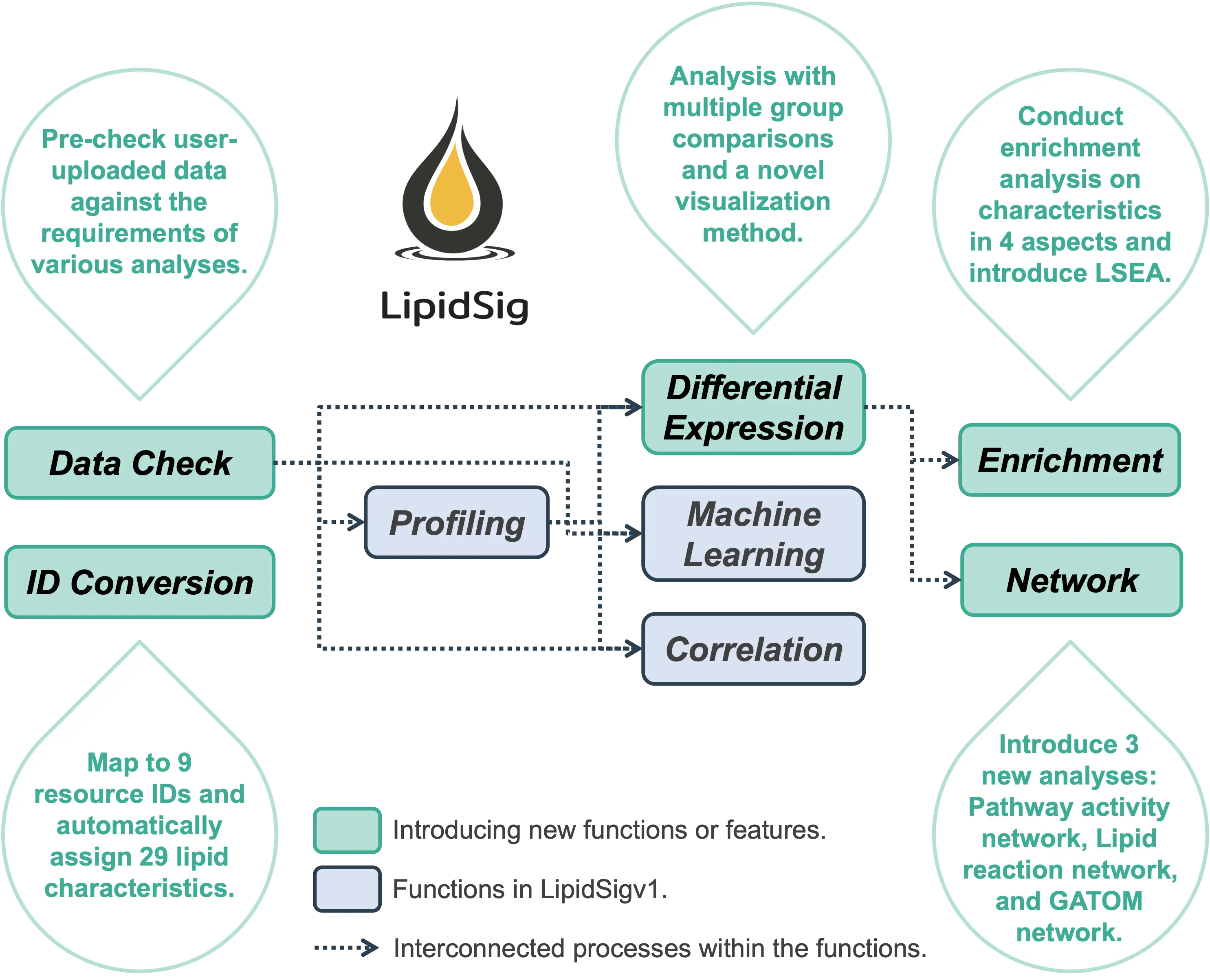
The user-friendly interface provides two helper functions, Data Check and ID Conversion, and six analytical functions: Profiling, Differential expression, Enrichment, Machine learning, Correlation, and Network.
-
The two helper functions offer format verification for user-uploaded data, map to 9 resource IDs, and automatically assign 29 lipid characteristics based on the uploaded features.
-
The six analytical functions are designed for the assessment of lipid effects on biological mechanisms and provide unique aspects to analyze the lipidome profiling data based on different characteristics, including lipid class, chain length, unsaturation, hydroxyl group, and fatty acid composition.
Users can perform intensive lipid analysis and create interactive plots with downloadable images and corresponding tables.
- Main updates in LipidSig 2.0:
- Data Check (New Function) :
Enables pre-checking of user-uploaded data to ensure compliance with the requirements of various analyses.
- ID Conversion (New Function) :
Maps user-uploaded features to 9 resource IDs and automatically assigns 29 lipid characteristics.
- Differential Expression (Updated Function) :
Now offers analysis with multiple group comparisons and introduces a novel visualization method.
- Enrichment (New Function) :
Allows enrichment analysis of characteristics across four aspects, including introducing LSEA.
- Network (Updated Function):
Adds three new types of analyses - Pathway Activity Network, Lipid Reaction Network, and GATOM Network.
- Data Check (New Function) :
Enables pre-checking of user-uploaded data to ensure compliance with the requirements of various analyses. - ID Conversion (New Function) :
Maps user-uploaded features to 9 resource IDs and automatically assigns 29 lipid characteristics. - Differential Expression (Updated Function) :
Now offers analysis with multiple group comparisons and introduces a novel visualization method. - Enrichment (New Function) :
Allows enrichment analysis of characteristics across four aspects, including introducing LSEA. - Network (Updated Function):
Adds three new types of analyses - Pathway Activity Network, Lipid Reaction Network, and GATOM Network.
FAQ 2: What is the workflow of LipidSig?
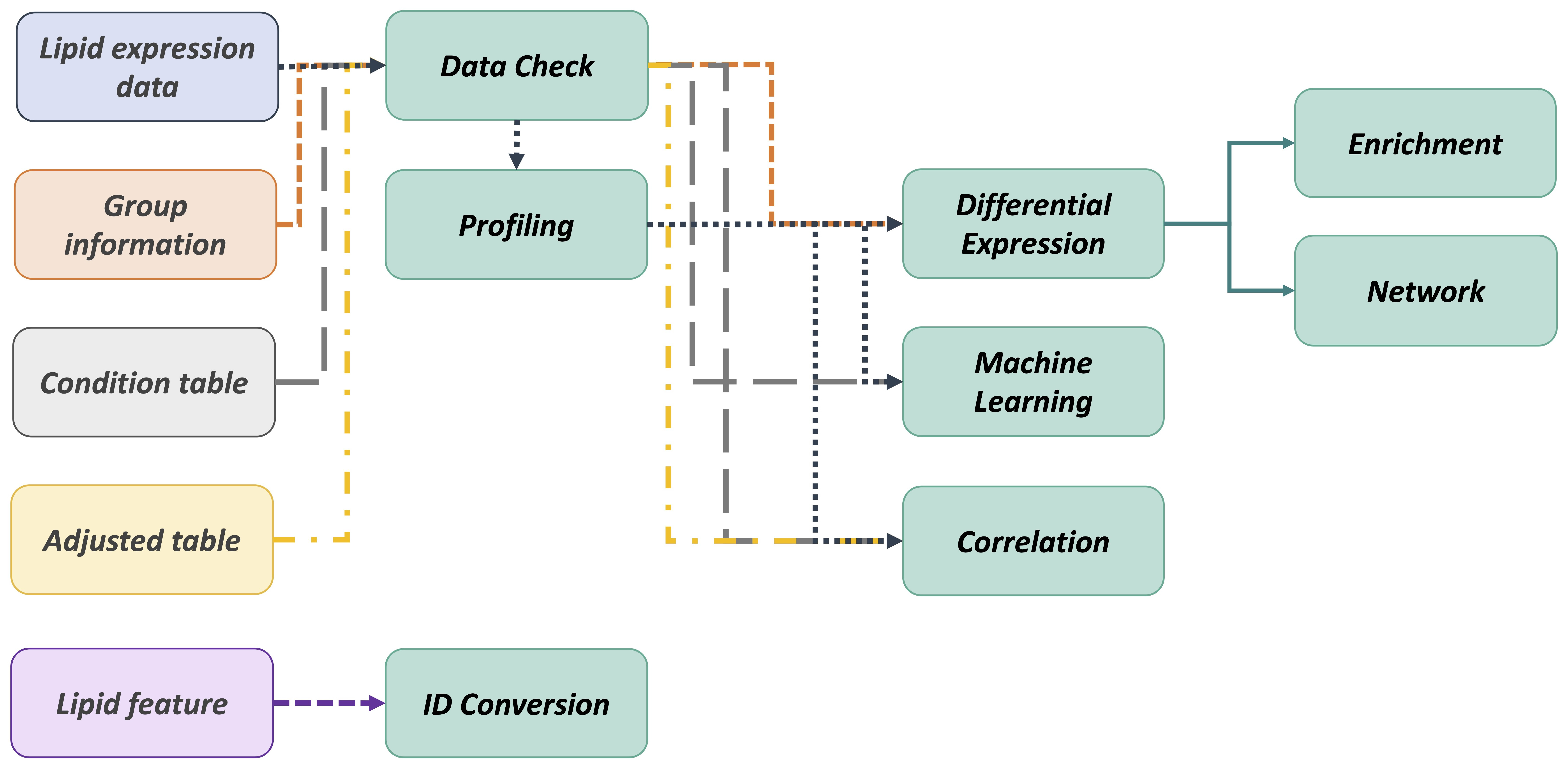
- The workflow of LipidSig is consists of four parts: (i) Data upload, (ii) Lipid characteristics transformation, (iii) Data processing, and (iv) Functionality and Visualization. After uploading the required matrices, users can select and adjust suitable parameters for following steps through a user-friendly interface. LipidSig has built-in lipid species and lipid characteristics two different pipelines that can be freely converted. LipidSig also supports six independent functions and concise visualization to profile lipid abundance, identify significant features, or construct an informative network.

FAQ 3: How do I begin using LipidSig?
-
The flowchart below outlines the recommended approach for utilizing our platform.
-
We recommend you first check your uploaded data on the Data Check webpage. It will review the data format and guide you on fixing the error.
-
After checking all the data formats are correct, you can proceed to the Profiling analysis for a comprehensive overview of your lipid abundance data.
-
Subsequently, you can continue the Differential Expression, Machine Learning, and Correlation analyses to explore and identify significant lipid species or characteristics.
-
Then, the Differential Expression analysis results can further serve as input for conducting Enrichment and Network analyses.
-
Additionally, our platform provides an ID conversion function, mapping 9 resource ID and automatically assigning 29 lipid characteristics to your input features.

FAQ 4: Does LipidSig provide demo dataset?
-
Yes, for each section, LipidSig provides various examples from previous papers for researchers to explore functions.
You can experiment with our demo dataset by selecting it from each webpage's data input control panel.
-
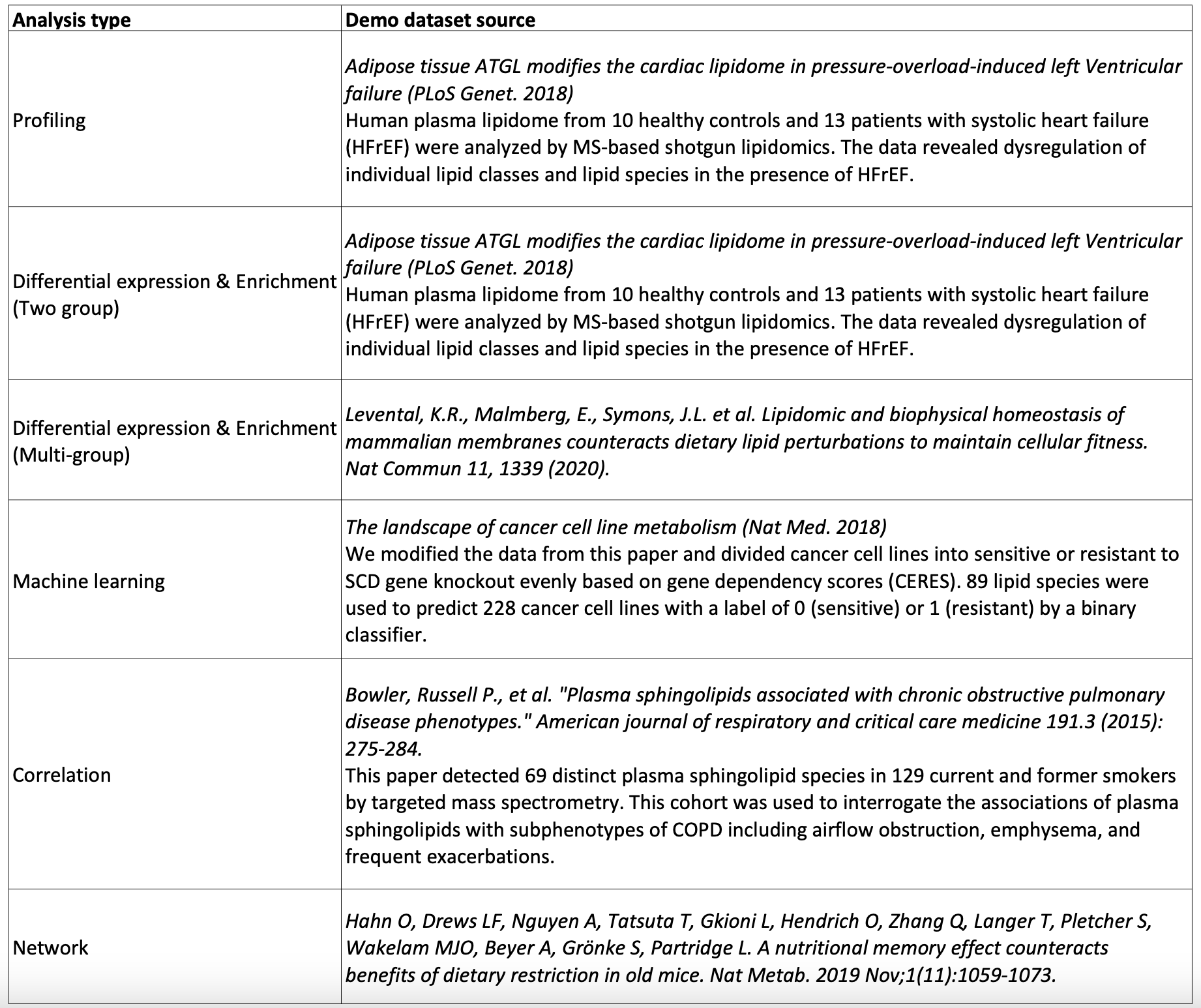
The demo datasets' sources corresponding to each analysis type are listed below.
You can experiment with our demo dataset by selecting it from each webpage's data input control panel.

FAQ 5: How do I prepare my dataset for analysis?
-
This page describes the guidance for preparing input data specifically for Profiling, Differential Expression, Machine Learning, and Correlation analyses.
For preparing input data for Enrichment and Network analyses, please refer to the next FAQ.
-
Below is a table outlining the specific data requirements for each type of analysis.
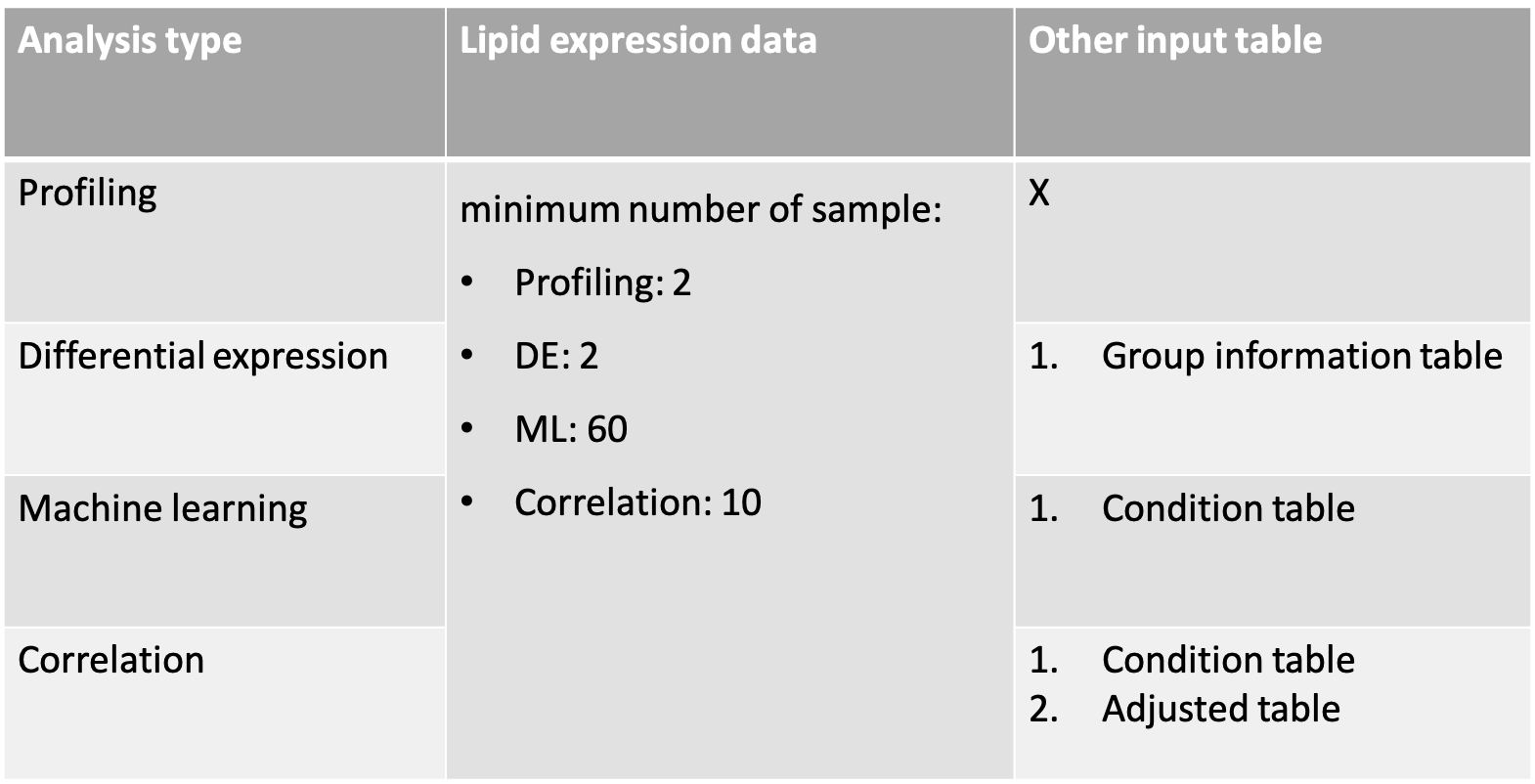
Lipid abundance data is required for all analyses, but the minimum number of samples required differs for each analysis type.
-
If you want to check your data's format accuracy, use the Data Check webpage on our platform.
It provides an overall examination of your data format. Detailed guidance on using the Data Check webpage can be found in the Tutorial.
-
In the following sections, we will describe the format requirements that must be adhered to for each dataset.
- Lipid abundance data
The lipid abundance data includes the abundance values of each feature across all samples.
The screenshot below shows an example with 3 samples in both the control and experimental groups.
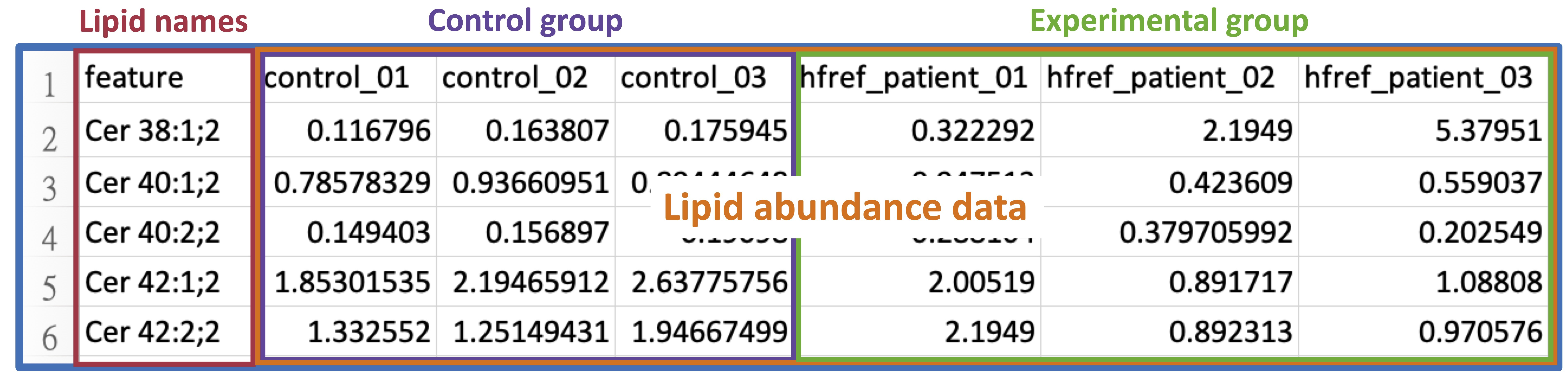
Lipid abundance data must adhere to the following format requirements.
- The file should be saved in CSV format.
- The first column of abundance data must contain a list of lipid names (features).
- Each lipid name (feature) is unique. We advise using Shorthand notation or referencing styles from HMDB, SwissLipids, and LIPID MAPS LMSD for input.
For a detailed explanation, please refer to FAQ.
- All abundance values are numeric.
- Group information table
The group information table contains the grouping details corresponding to the samples in lipid abundance data.
It comprises the sample's name, the sample's label, the group name of the sample, and the pair number (only required for two-group data), which denotes the specific pairing used for the t-test/Wilcoxon test.
Take two-group data for example. The screenshot below shows an example with 3 samples in both the control and experimental groups.

Group information table must adhere to the following format requirements. Please note that the table formats for two-group data and multi-group data have different restrictions.
Two group:
- The file should be saved in CSV format.
- The column names are arranged in order of sample_name, label_name, group, and pair.
- All sample names are unique.
- Sample names in 'sample_name' column are as same as the sample names in lipid abundance data.
- Columns of 'sample_name', 'label_name', and 'group' columns do not contain NA values.
- The column 'group' contain 2 groups.
- In the 'pair' column for paired data, each pair must be sequentially numbered from 1 to N, ensuring no missing, blank, or skipped numbers are missing; otherwise, the value should be all marked as NA.
Multi-group:
- The file should be saved in CSV format.
- The column names are arranged in order of sample_name, label_name, and group.
- All sample names are unique.
- Sample names in 'sample_name' column are as same as the sample names in lipid abundance data.
- All columns do not contain any missing value.
- The column 'group' contain more than 2 groups.
- Condition table (for Machine learning analysis)
To create the condition table, you should have lipid abundance and demographic data available.
Take the COPD dataset as an example, shown below.
The 'Lipid Abundance Data' table comprises 8 samples and their corresponding Lipid features, such as sphingolipids.

The 'Demographic' data encompasses various clinical attributes, including age, sex, BMI, clinical subphenotypes of COPD, symptoms, etc.
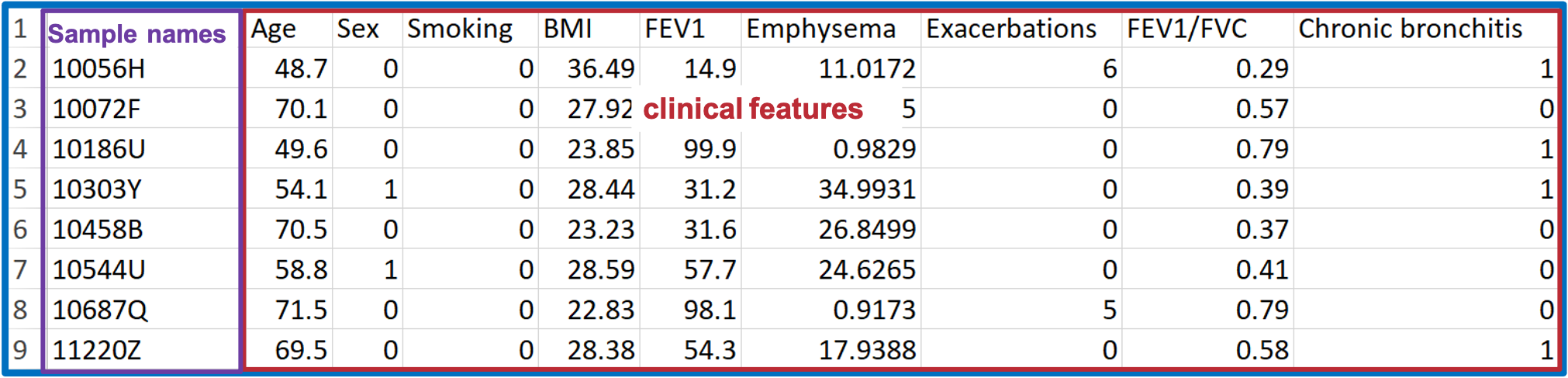
For constructing the condition table, select one clinical term (or one set of clinical terms) from the demographic data and assign a group number to each sample. This group number should be either 0 or 1.
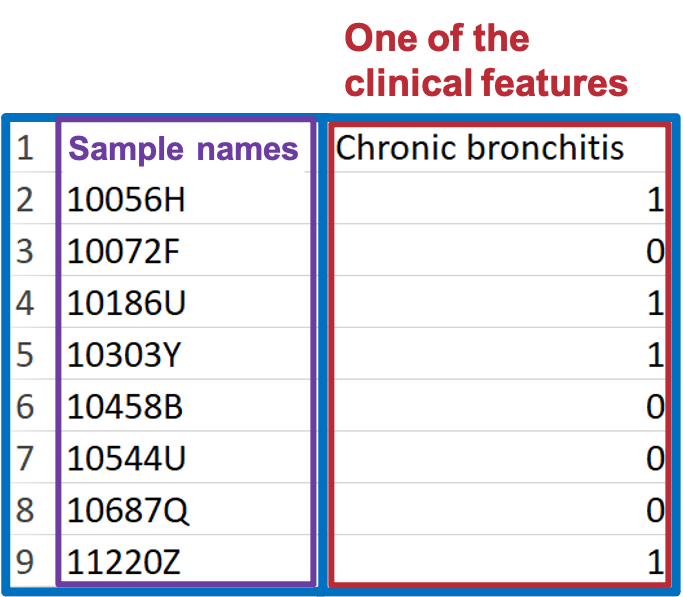
Condition table must adhere to the following format requirements.
- The file should be saved in CSV format.
- The column names must be arranged in order of 'sample_name' and 'group'.
- Sample names 'sample_name' column must be as same as the sample names in lipid abundance data.
- The column 'group' must be numeric (only be 0 or 1).
- Each group must have more than 30 samples.
- Condition table and Adjusted table (for Correlation analysis)
To create the condition table and adjusted table, you should have lipid abundance and demographic data available.
Take the COPD dataset as an example, shown below.
The 'Lipid Abundance Data' table comprises eight samples and their corresponding Lipid features, such as sphingolipids.
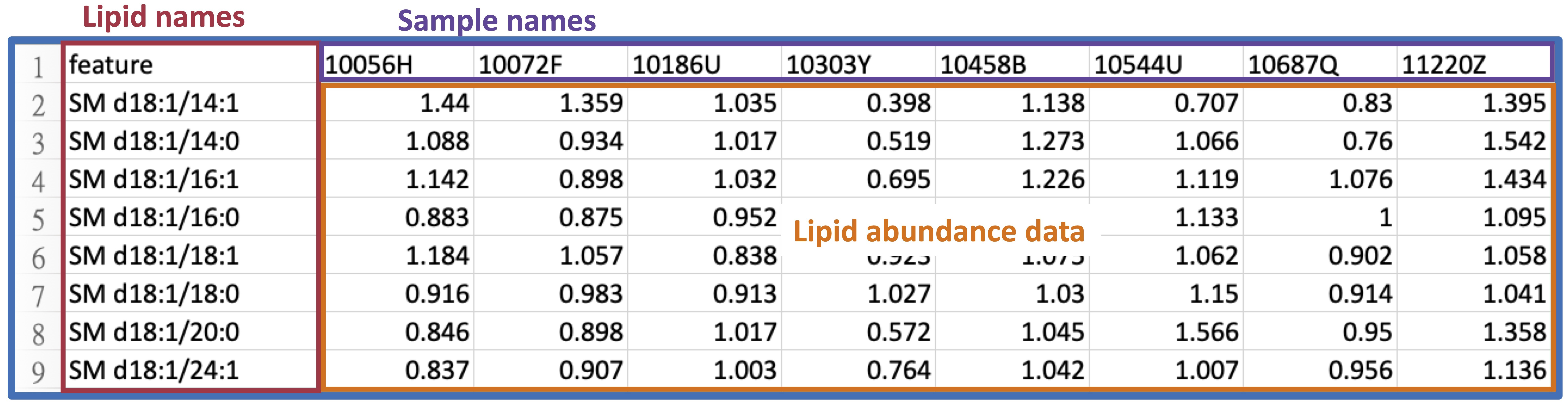
The 'Demographic' data encompasses various clinical attributes, including age, sex, BMI, clinical subphenotypes of COPD, symptoms, etc.
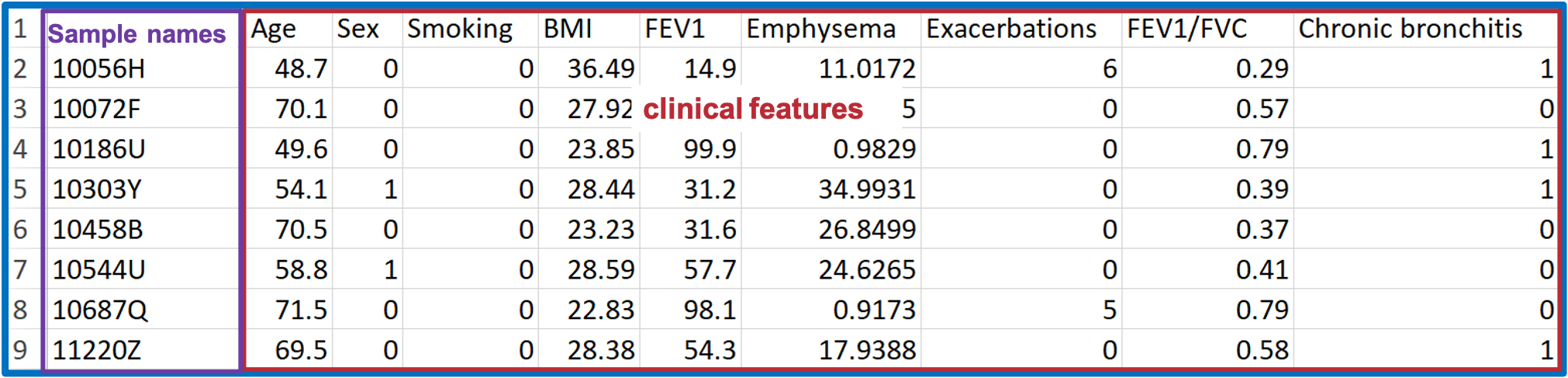
For constructing the condition table, select desired clinical terms (i.e., clinical subphenotypes of COPD) from demographic data.
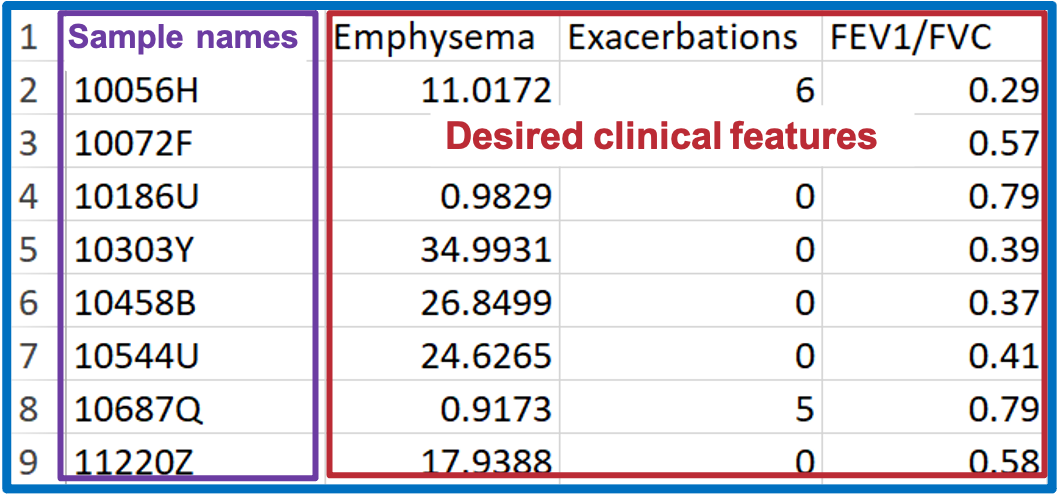
Condition table must adhere to the following format requirements.
- The file should be saved in CSV format.
- The first column name must be 'sample_name'.
- Sample names 'sample_name' column must be as same as the sample names in lipid abundance data.
- The column 'sample_name' must contain character values.
- All the columns must be numeric (except 'sample_name' column).
- Must contain at least 2 conditions.
For constructing the adjusted table, pick the clinical terms from the demographic table that will be corrected in linear or logistic regression analysis.

Adjusted table must adhere to the following format requirements.
- The file should be saved in CSV format.
- The first column name must be 'sample_name'.
- Sample names 'sample_name' column must be as same as the sample names in lipid abundance data.
- The column 'sample_name' must contain character values.

Lipid abundance data is required for all analyses, but the minimum number of samples required differs for each analysis type.
- Lipid abundance data
The lipid abundance data includes the abundance values of each feature across all samples. The screenshot below shows an example with 3 samples in both the control and experimental groups.

Lipid abundance data must adhere to the following format requirements.- The file should be saved in CSV format.
- The first column of abundance data must contain a list of lipid names (features).
- Each lipid name (feature) is unique. We advise using Shorthand notation or referencing styles from HMDB, SwissLipids, and LIPID MAPS LMSD for input. For a detailed explanation, please refer to FAQ.
- All abundance values are numeric.
- Group information table
The group information table contains the grouping details corresponding to the samples in lipid abundance data. It comprises the sample's name, the sample's label, the group name of the sample, and the pair number (only required for two-group data), which denotes the specific pairing used for the t-test/Wilcoxon test.
Take two-group data for example. The screenshot below shows an example with 3 samples in both the control and experimental groups.

Group information table must adhere to the following format requirements. Please note that the table formats for two-group data and multi-group data have different restrictions.- Two group:
- The file should be saved in CSV format.
- The column names are arranged in order of sample_name, label_name, group, and pair.
- All sample names are unique.
- Sample names in 'sample_name' column are as same as the sample names in lipid abundance data.
- Columns of 'sample_name', 'label_name', and 'group' columns do not contain NA values.
- The column 'group' contain 2 groups.
- In the 'pair' column for paired data, each pair must be sequentially numbered from 1 to N, ensuring no missing, blank, or skipped numbers are missing; otherwise, the value should be all marked as NA.
- Multi-group:
- The file should be saved in CSV format.
- The column names are arranged in order of sample_name, label_name, and group.
- All sample names are unique.
- Sample names in 'sample_name' column are as same as the sample names in lipid abundance data.
- All columns do not contain any missing value.
- The column 'group' contain more than 2 groups.
- Condition table (for Machine learning analysis)
To create the condition table, you should have lipid abundance and demographic data available.
Take the COPD dataset as an example, shown below. The 'Lipid Abundance Data' table comprises 8 samples and their corresponding Lipid features, such as sphingolipids.

The 'Demographic' data encompasses various clinical attributes, including age, sex, BMI, clinical subphenotypes of COPD, symptoms, etc.

For constructing the condition table, select one clinical term (or one set of clinical terms) from the demographic data and assign a group number to each sample. This group number should be either 0 or 1.

Condition table must adhere to the following format requirements.- The file should be saved in CSV format.
- The column names must be arranged in order of 'sample_name' and 'group'.
- Sample names 'sample_name' column must be as same as the sample names in lipid abundance data.
- The column 'group' must be numeric (only be 0 or 1).
- Each group must have more than 30 samples.
- Condition table and Adjusted table (for Correlation analysis)
To create the condition table and adjusted table, you should have lipid abundance and demographic data available.
Take the COPD dataset as an example, shown below.
The 'Lipid Abundance Data' table comprises eight samples and their corresponding Lipid features, such as sphingolipids.

The 'Demographic' data encompasses various clinical attributes, including age, sex, BMI, clinical subphenotypes of COPD, symptoms, etc.

For constructing the condition table, select desired clinical terms (i.e., clinical subphenotypes of COPD) from demographic data.

Condition table must adhere to the following format requirements.- The file should be saved in CSV format.
- The first column name must be 'sample_name'.
- Sample names 'sample_name' column must be as same as the sample names in lipid abundance data.
- The column 'sample_name' must contain character values.
- All the columns must be numeric (except 'sample_name' column).
- Must contain at least 2 conditions.
For constructing the adjusted table, pick the clinical terms from the demographic table that will be corrected in linear or logistic regression analysis.

Adjusted table must adhere to the following format requirements.- The file should be saved in CSV format.
- The first column name must be 'sample_name'.
- Sample names 'sample_name' column must be as same as the sample names in lipid abundance data.
- The column 'sample_name' must contain character values.
FAQ 6: How can I obtain the required input for network and enrichment analysis?
-
For the enrichment analysis and network analysis (pathway activity network, lipid reaction network, and GATOM network), it is essential to use results from differential expression analysis as input data.
To ensure compatibility and reduce the likelihood of format errors, we strongly recommend using results obtained from the differential expression analysis of our platform.
-
Follow the steps in the screenshot below to obtain the differential expression analysis results.
- Navigate to the 'Differential Expression' analysis webpage.
- Upload your data and allow time for the format-checking process.
- Configure the settings for data processing.
- Review the processed data and click the 'Start' button to proceed.

- Define the conditions for the differential analysis and click the 'Start' button to begin the analysis.
- Visit the results download page and download the analysis results.
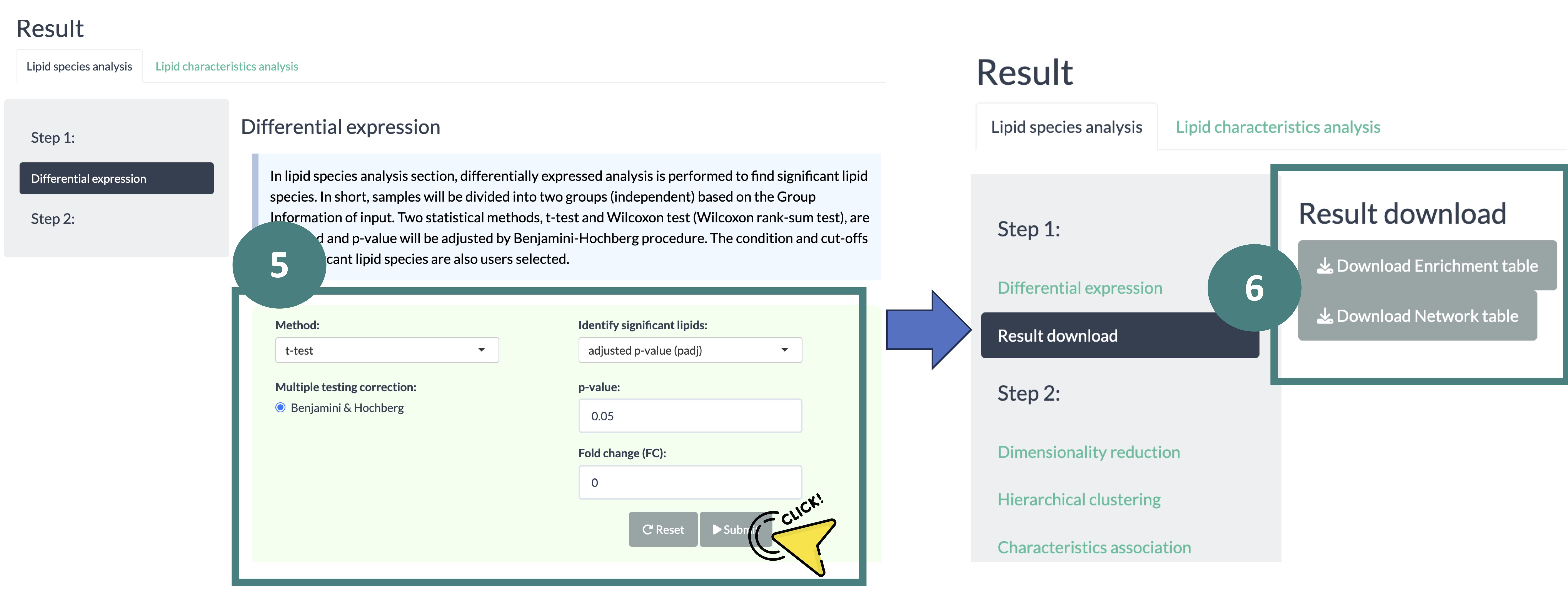
- Once you have downloaded the results, proceed to the enrichment or network analysis webpage and upload the necessary data as required.
- Navigate to the 'Differential Expression' analysis webpage.
- Upload your data and allow time for the format-checking process.
- Configure the settings for data processing.
- Review the processed data and click the 'Start' button to proceed.
- Define the conditions for the differential analysis and click the 'Start' button to begin the analysis.
- Visit the results download page and download the analysis results.


FAQ 7: How to upload my dataset?
-
For Profiling, Differential Expression, Machine Learning, and Correlation analyses, please follow the instructions below for data uploading. For Enrichment and Network analysis, refer to the earlier FAQ.
-
You will find a panel on each analysis webpage detailing the specific tables needed for those analyses.
-
Take “Differential Expression analysis” for example.
-
Click on the “Upload your data” button, upload your data, and wait for the format-checking process.
Then, the uploaded data will displayed on the right-hand side of the screen.
The format-checking results are shown below.
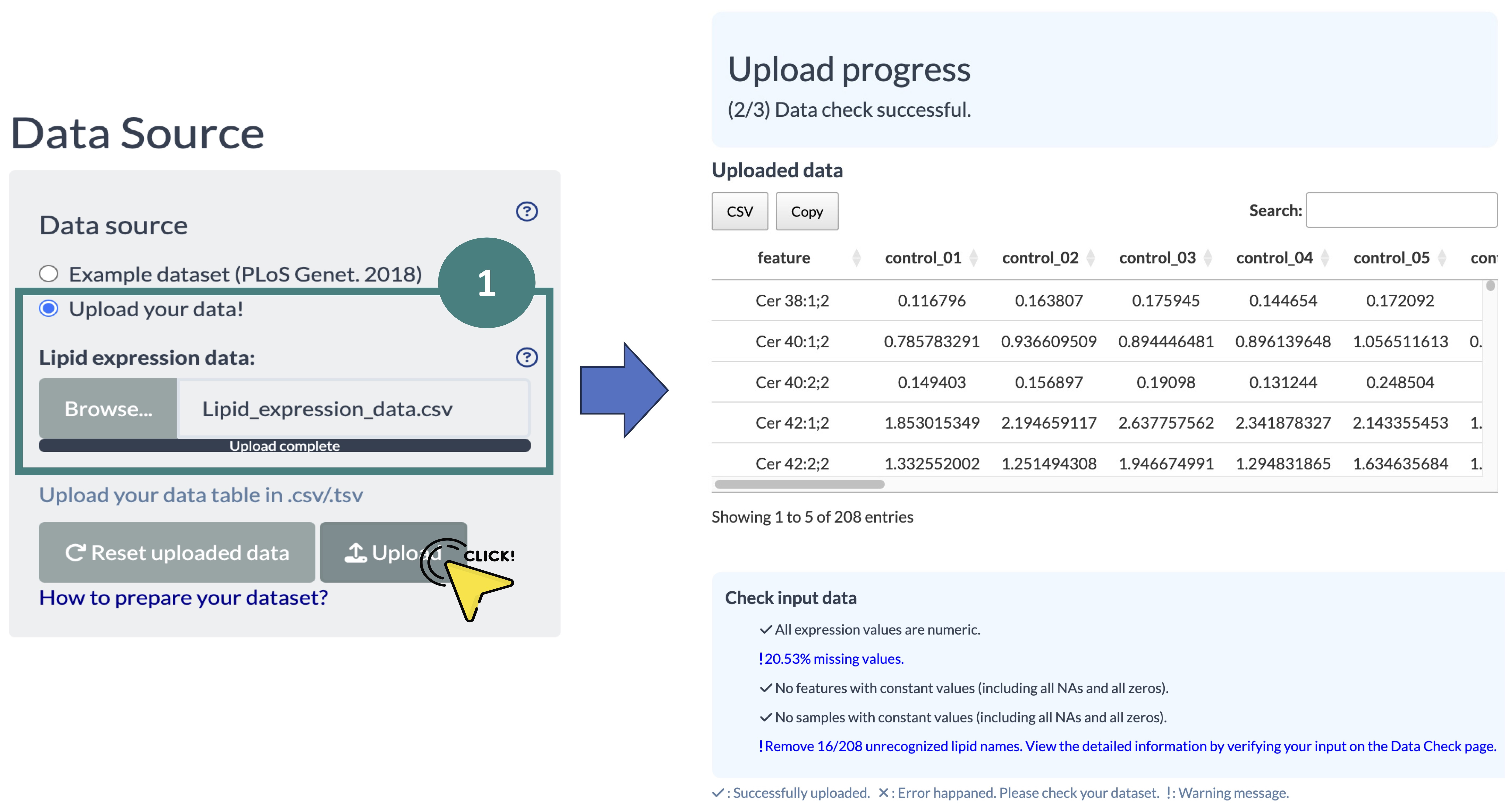
If the checking result indicates 'Incorrect data format' show as below screenshot, please refer to the Data Check webpage for a detailed examination.

-
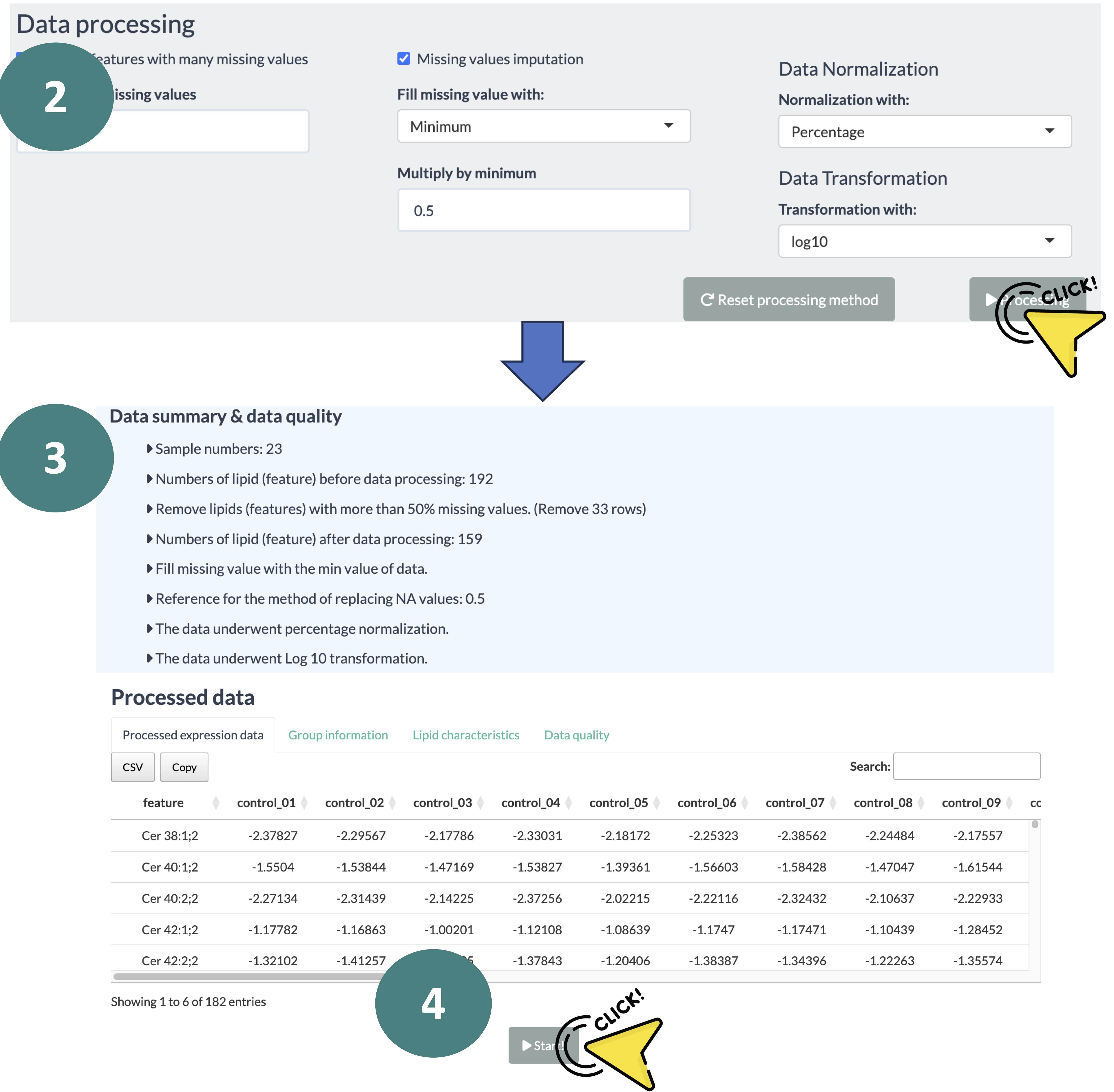
Configure the settings for data processing.
-
After data processing, you will receive a data summary about the processing details of uploaded data, the processed abundance data, and a conversed lipid characteristic table according to the features in the uploaded abundance data.
Review the data to ensure everything is correct.
-
Click the 'Start' button to begin the analysis.
-
Click on the “Upload your data” button, upload your data, and wait for the format-checking process.
Then, the uploaded data will displayed on the right-hand side of the screen.
The format-checking results are shown below.

If the checking result indicates 'Incorrect data format' show as below screenshot, please refer to the Data Check webpage for a detailed examination.
- Configure the settings for data processing.
- After data processing, you will receive a data summary about the processing details of uploaded data, the processed abundance data, and a conversed lipid characteristic table according to the features in the uploaded abundance data. Review the data to ensure everything is correct.
- Click the 'Start' button to begin the analysis.

FAQ 8: What kinds of lipidome specific analyses that LipidSig provides?
- In LipidSig 2.0, we introduce an ID conversion function that maps user-uploaded features to 9 resource IDs and automatically assigns 29 lipid characteristics. Additionally, the Differential Expression Analysis section now includes the two-characteristic analysis, offering heatmaps that depict the correlation between double bonds and chain lengths of lipid species. In the network analysis section, we have added three new networks, GATOM Network, Pathway Activity Network, and Lipid Reaction Network, to facilitate a more comprehensive exploration.
- It is easy to use these lipidome specific analyses. A simple example of using lipidome specific analyses in the ‘Differential expression’ section will be addressed as follow. Firstly, in “Step 1”, the ‘Lipid characteristics analysis’ utilise two-way ANOVA to assist users to find the significant lipid species splitting by the lipid characteristics that user-chosen, such as class, total length. After submission, the difference between these characteristics will be displayed by bar charts, line chart and box plots. Next, in “Step 2”, ‘Dimensionally reduction’ and ‘Hierarchical clustering’ help researchers to discover crucial properties of the lipid data are revealed and still close to its intrinsic characteristics.
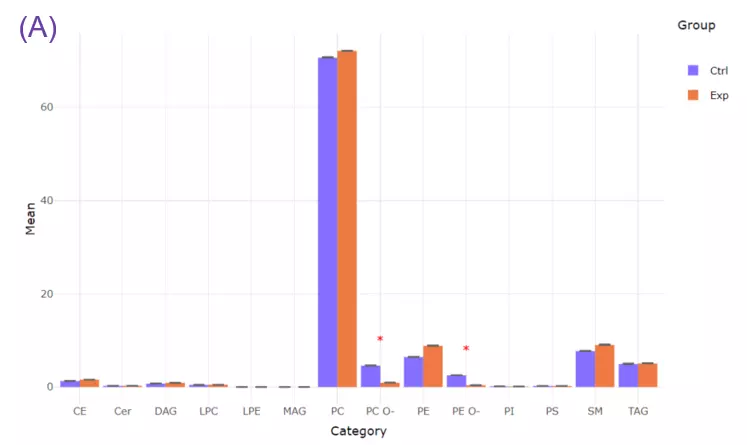
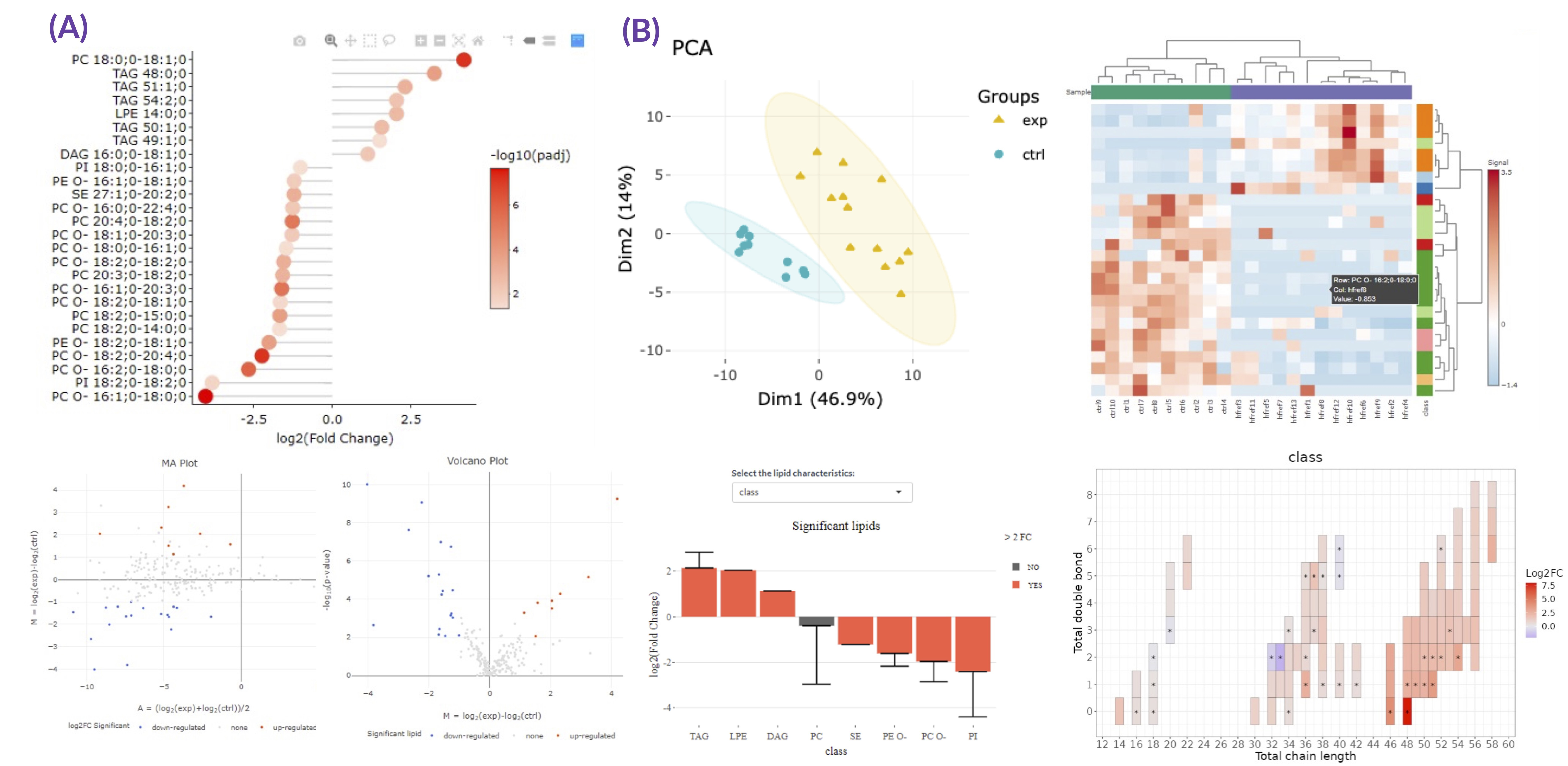
- To exemplify more specifically, lipid class and shape belong to structure-based features and provide an overview of altered lipid metabolism pathways. As shown in Figures A, downregulation of PC O- and PE O- class indicated inhibition of ether lipid biosynthesis pathway.
- On the other hand, we can calculate the numbers of the double bond, chain length, and hydroxyl group that comprise fatty acid diversity. The double bond change reflects membrane unsaturation degree or fluidity and has been connected to signaling transduction (Bi et al., 2019; Levental et al., 2017).
- Recent findings revealed C16:0 ceramide could lead to insulin resistance in obesity, unravelling a new role of specific chain length (Figures B) (Holm et al., 2019; Turpin et al., 2014).
- Moreover, LipidSig also provides an analysis focusing on individual fatty acid instead of lipid species. This allows users to examine different types of polyunsaturated fatty acids (PUFAs) that are stored in lipids and exert special functions. For instance, compared to calculation results of total double bonds in lipid species, an increase in fatty acids with 6 double bonds was more convincible by DHA supplementation (Figure C). PUFA search through fatty acid analysis can be used to explore substrate specificity of acyltransferases, too (Yamashita et al., 2014).
- Further, our web server also enables users to define lipids containing unique PUFAs directly and observe their change (Supplemental Figures S2C) (Kandice R. Levental et al., 2020; Levental et al., 2017).
- Another appealing tool in LipidSig is multiple lipid characteristics analysis. Two factors interaction can be achieved in Differential expression section and is very suitable for the studies that concentrate on specific reactions or pathways. Related applications include PC saturation remodelling catalyzed by LPCAT1 in cancers (Bi et al., 2019)
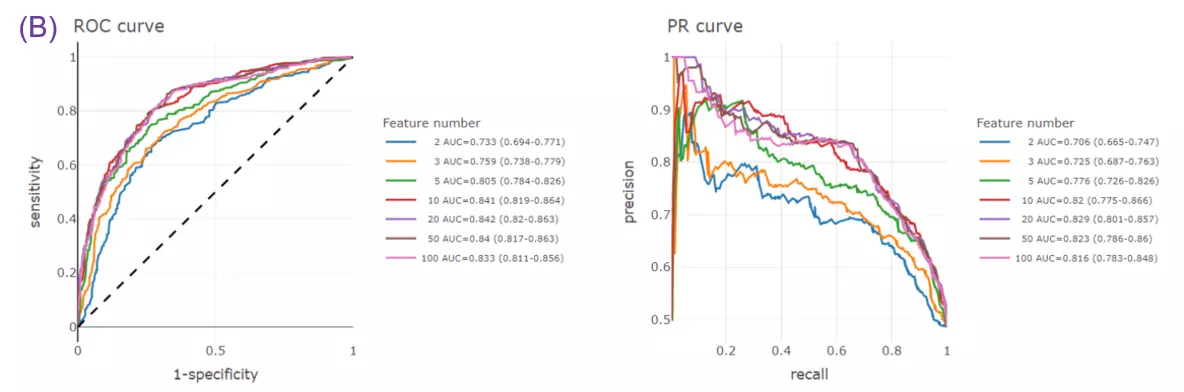
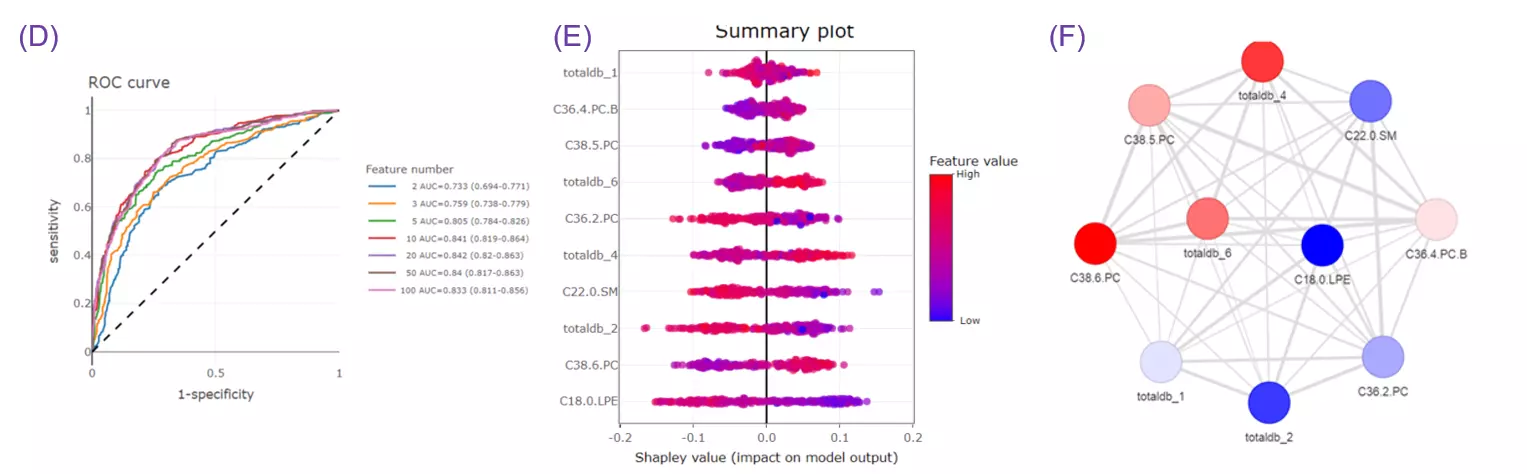
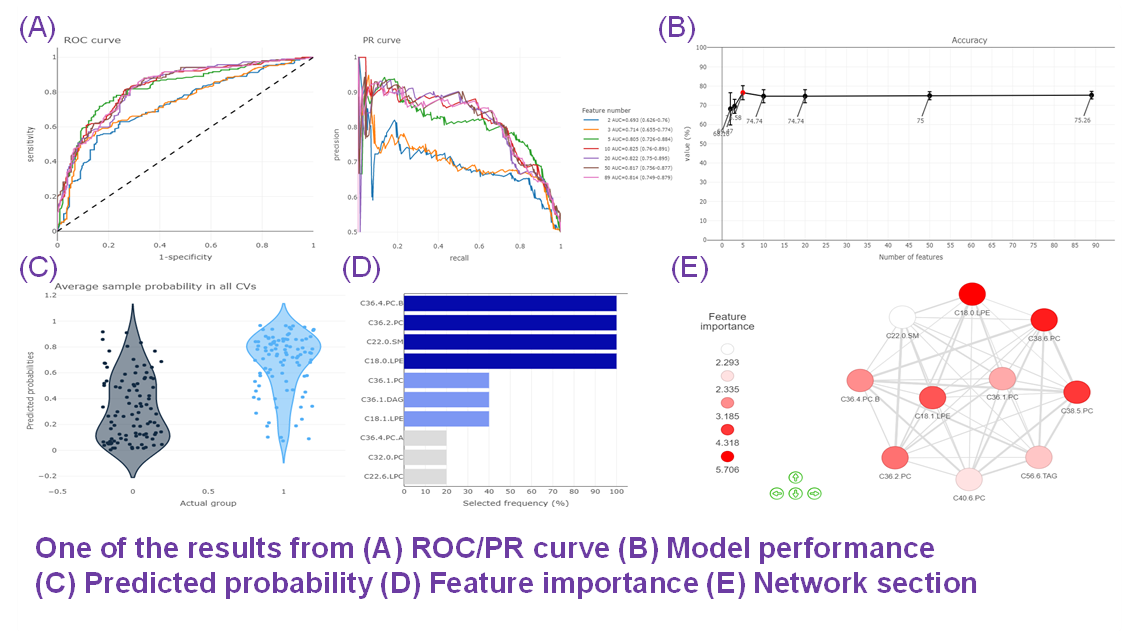
- Given more than two characteristics, users are encouraged to build different machine learning models to evaluate the importance of lipid-related variables. Characteristics introduction can increase the structural or functional resolution of the lipidome and have been used in clinical research (Gerl et al., 2019; Poss et al., 2020) and our example to further improve the model prediction (Figure D-F).


FAQ 9: When to use these analyses? What is the difference?
-
The two helper functions, Data check and ID conversion, offer format verification, resource ID mapping and lipid characteristics assignment.
-
Data Check page is specifically designed to pre-check user-uploaded data against the requirements of Profiling, Differential Expression, Machine Learning, and Correlation analyses.
It will return checking results according to the data needs of specific analysis types.
-
ID conversion function is designed to map to 9 resource IDs, and automatically assign 29 lipid characteristics. Once the input features are converted, the uploaded, recognized, and unrecognized features will displayed.
- Data Check page is specifically designed to pre-check user-uploaded data against the requirements of Profiling, Differential Expression, Machine Learning, and Correlation analyses. It will return checking results according to the data needs of specific analysis types.
- ID conversion function is designed to map to 9 resource IDs, and automatically assign 29 lipid characteristics. Once the input features are converted, the uploaded, recognized, and unrecognized features will displayed.
- The six analytical functions provide Profiling, Differential expression, Enrichment, Machine learning, Correlation, and Network analyses for assessment of lipid effects on biological mechanisms.
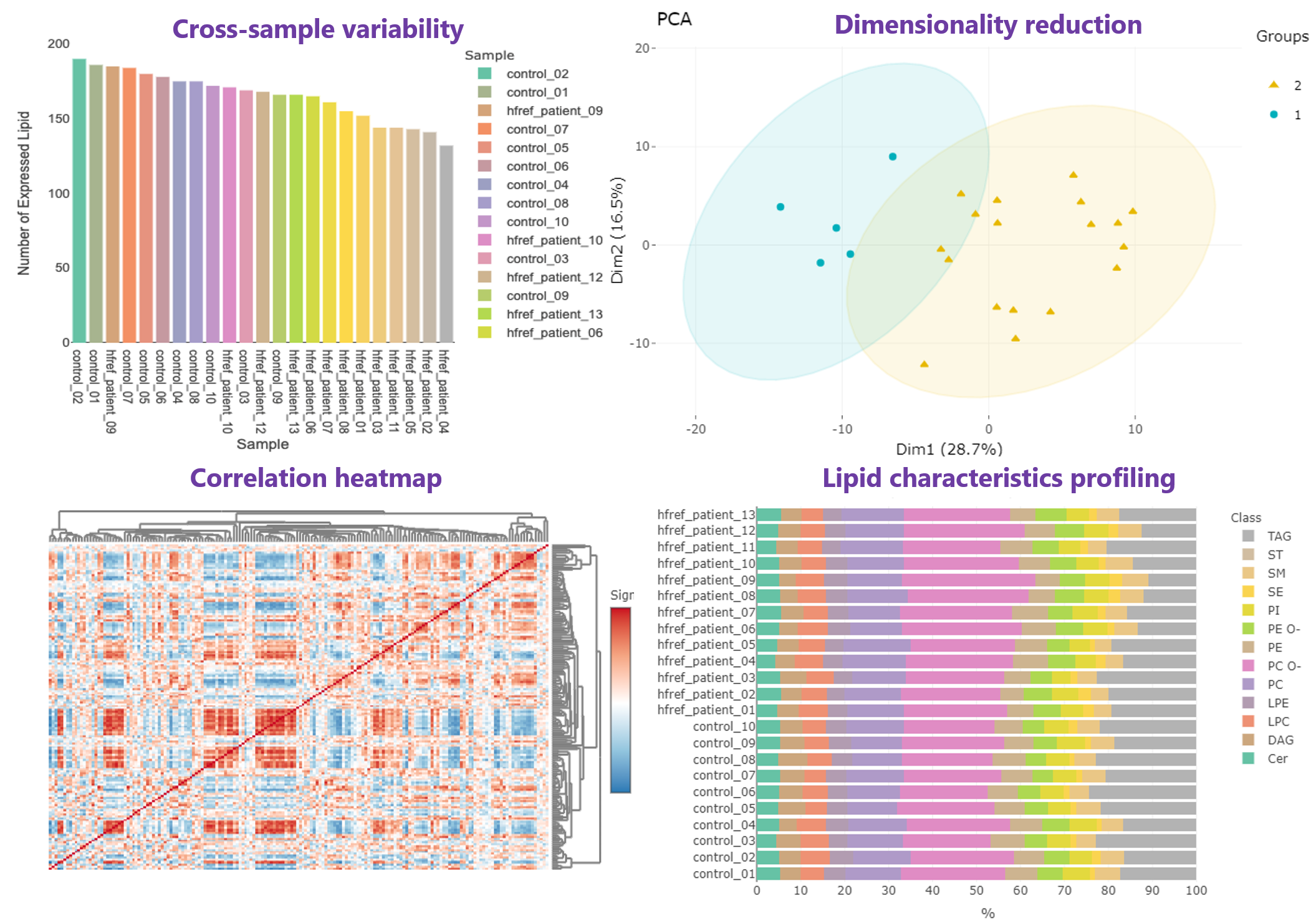
- In Profiling page, an overview gathering comprehensive analyses are offered for high-throughput screening, allowing researchers to efficiently explore the quality and the clustering of samples,correlation between lipids and samples, and the lipid abundance and composition.
- An application of lipid profiling can be found in Grzybek, Michal, et al. "Comprehensive and quantitative analysis of white and brown adipose tissue by shotgun lipidomics." Molecular metabolism 22 (2019): 12-20.
- Differential expression section assists users to identify significant lipid species or lipid characteristics (Fig.A). By utilising user-defined methods and characteristics, dimensionality reduction, hierarchical clustering, characteristics analysis, and two characteristic analysis (Fig.B) can be implemented based on the results of differential expressed analysis.
- Three examples of using differential expression analyses in lipid study:
- By Species :
- Zou, Yilong, et al. "Plasticity of ether lipids promotes ferroptosis susceptibility and evasion." Nature 585.7826 (2020): 603-608.
- By Characteristics :
- Levental, Kandice R., et al. "ω-3 polyunsaturated fatty acids direct differentiation of the membrane phenotype in mesenchymal stem cells to potentiate osteogenesis." Science advances 3.11 (2017): eaao1193.
- Hammerschmidt, Philipp, et al. "CerS6-derived sphingolipids interact with Mff and promote mitochondrial fragmentation in obesity." Cell 177.6 (2019): 1536-1552.
- Enrichment provides two main approaches: 'Over Representation Analysis (ORA)' and 'Lipid Set Enrichment Analysis (LSEA)'. ORA analysis illustrates significant lipid species enriched in the categories of lipid class. LSEA analysis is a computational method determining whether an a priori-defined set of lipids shows statistically significant, concordant differences between two biological states (e.g., phenotypes).
- In terms of the Machine learning analysis, this section comprises a broad variety of the user-defined feature selection methods and classifiers, as well as the other parameters for training the best model. It followed by a series of subsequent analyses to help users to evaluate the methods and visualise the results of machine learning.
- An example of using machine learning in lipidomics analysis:
- Gerl, Mathias J., et al. "Machine learning of human plasma lipidomes for obesity estimation in a large population cohort." PLoS biology 17.10 (2019): e3000443.
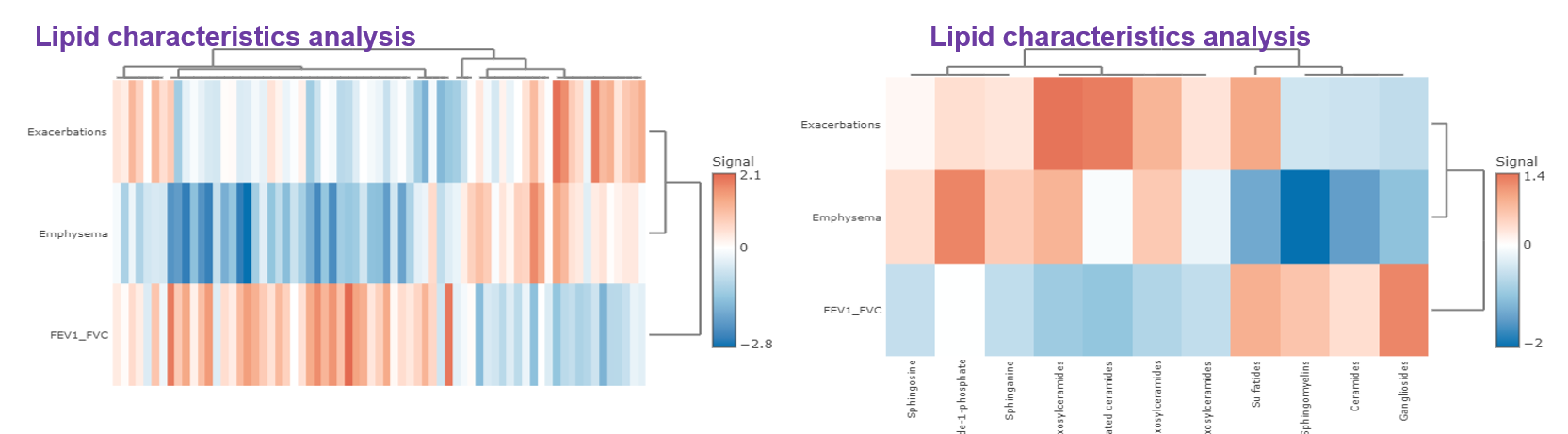
- Correlation analysis illustrates the relationship of the clinical features and the lipids species and other mechanistically relevant lipid characteristics, which has been applied to many fields of study, such as Bowler RP et al. discovering that sphingomyelins are strongly associated with emphysema and glycosphingolipids are associated with COPD exacerbations. Our platform provides diverse correlation, linear regression methods, and customised cut-offs to visualise the strength of association between clinical features and lipid species/characteristics.
-
As for
Network
, our platform constructs five distinct types of networks.
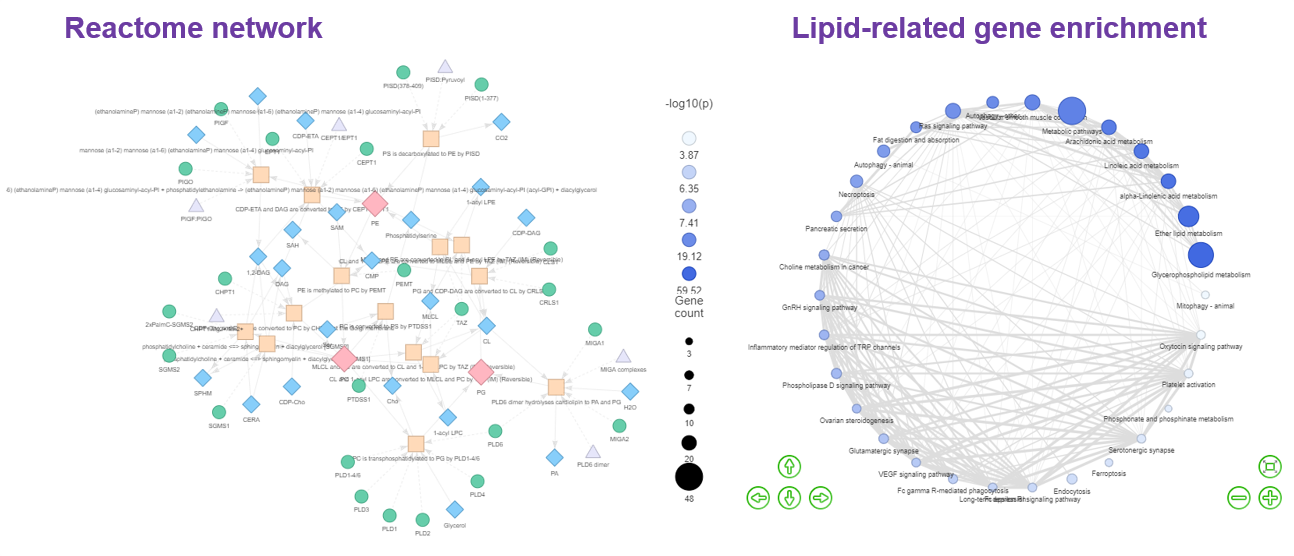
The ‘Reactome pathway’ and ‘Lipid-related gene enrichment’ to interrogate the lipid metabolism pathways and lipid-related gene enrichment. By selecting different lipid classes, researchers can discover the metabolic networks between small molecules within Reactome Network topologies and their interactions with proteins in the ‘Reactome pathway’ function. In ‘Lipid-related gene enrichment’, a multi-omics analysis is applied to display the association of the lipids with gene function and a similar method has been used to identify relevant pathways of altered metabolites. - An example of utilising Network to analyse fatty acid metabolism:
- Vantaku, Venkatrao, et al. "Multi-omics integration analysis robustly predicts high-grade patient survival and identifies CPT1B effect on fatty acid metabolism in bladder cancer." Clinical Cancer Research 25.12 (2019): 3689-3701.
- An example of utilising Network:
- A nutritional memory effect counteracts benefits of dietary restriction in old mice (Nat Metab. 2019).
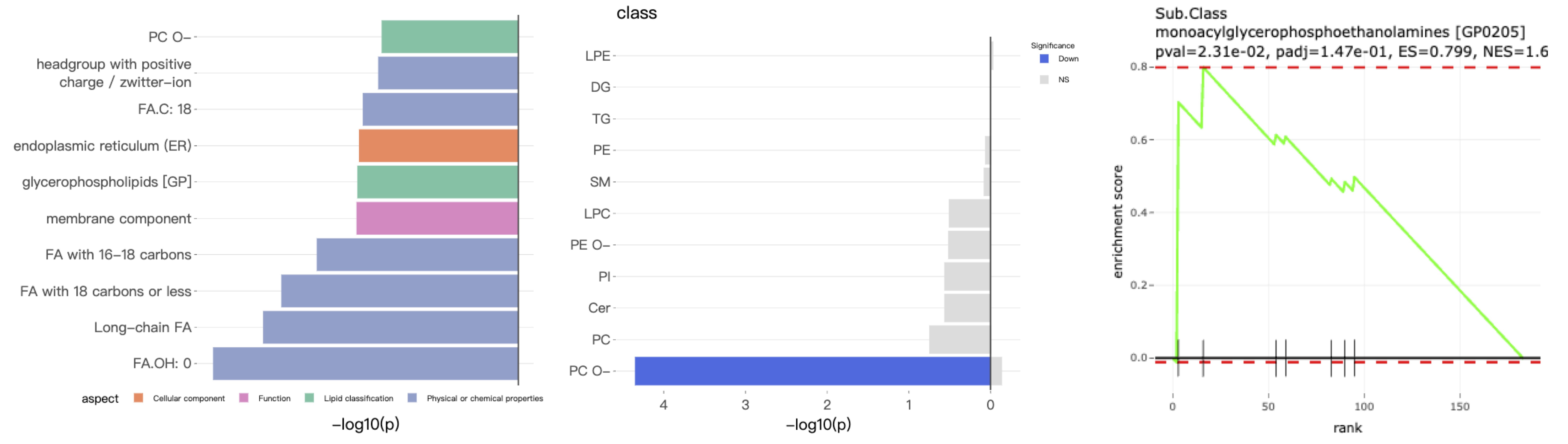
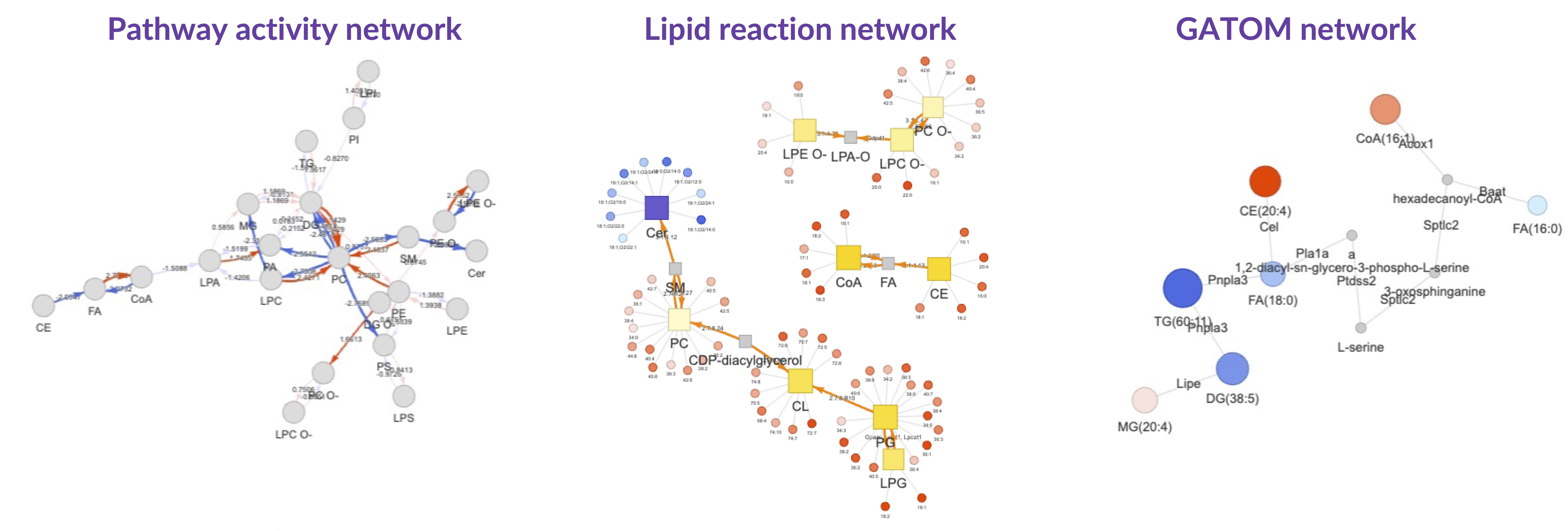
Results from "Differential Expression" are further analyzed using the "GATOM network", which isolates significant subnetworks within a constructed metabolite-level network. The "Pathway activity network" computes flux changes in the lipid reaction network, facilitating the identification of active or suppressed pathways. Lastly, the "Lipid reaction network" graphically represents significant lipid classes/species within lipid biosynthesis pathways.
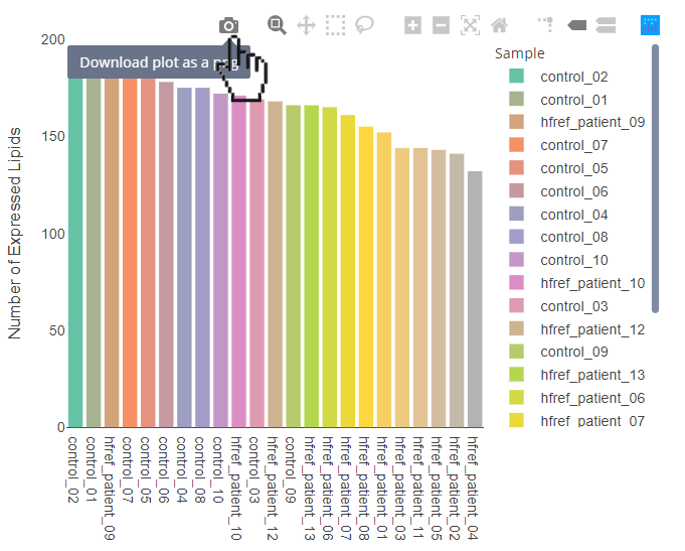
FAQ 10: Can I download these figures? How to manipulate interactive figures in LipidSig?
- Download the figure:
- Hover over the interactive figures to show tool bar. Press the camera icon on the far left.
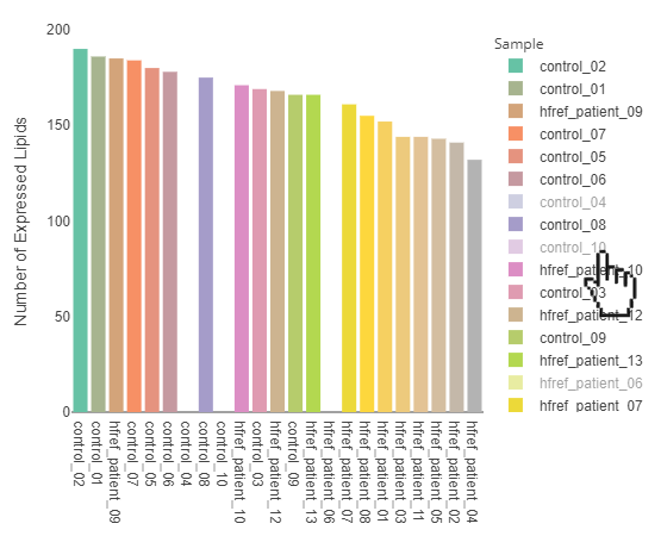
- Select specific sample types:
- By clicking the sample types of the legend, the specific sample types will be hid. By clicking the sample types again, the selected sample types will be shown on the plot.
- Adjust your zoom level:
- By clicking the second button from the left, users can circle the area that you want to zoom in.
- The ‘Plus’ button is for zoom in, while the ‘minus’ button is for zoom out.
- If you want to back to the original setting, press the house-like button to reset it.

FAQ 11: How is ID conversion performed? How can I understand the lipid characteristics converted from it?
-
LipidSig 2.0 streamlines lipid identification (ID) conversion, accommodating various ID types, including shorthand nomenclature, through its 'ID Conversion' feature.
This tool facilitates the conversion among nine distinct lipid IDs by an ID-integration table, merged from three primary sources: LIPID MAPS, SwissLipids, and MetaNetX.
It supports IDs such as shorthand notation, LIPID MAPS ID, LipidBank ID, HMDB ID, ChEBI ID, KEGG ID, and PubChem ID from LIPID MAPS, along with SwissLipids ID from SwissLipids, and MetaNetX ID from MetaNetX.
-
Leveraging Goslin, it recognizes shorthand notations, integrating more than 16,000 IDs from LIPID MAPS, more than 700,000 from MetaNetX, and more than 750,000 from SwissLipids into a unified table.
In detail, firstly, three overlapping IDs (LIPID MAPS ID, HMDB ID, and ChEBI ID) between LIPID MAPS and SwissLipids are used to integrate LIPID MAPS and SwissLipids.
The MetaNetX ID, which overlaps between SwissLipids and MetaNetX, merges MetaNetX into the integration table.
-
Uploading your data in the ID conversion function or within analysis functions (Profiling, Differential Expression, Machine Learning, and Correlation) on LipidSig will generate 29 lipid characteristics.
-
Here, we provide the table with each characteristic's aspect, characteristic, description, and source.
| Aspect | Characteristic | Description | Source | Differential expression analysis | Enrichment analysis |
|---|---|---|---|---|---|
| Lipid classification | Class | Lipid class abbreviation. | Goslin | v | v |
| Fatty acid properties | Total.FA | Specification of total fatty acid chains. | Goslin | v | v |
| Fatty acid properties | Total.C | Total number of chain lengths. | Goslin | v | v |
| Fatty acid properties | Total.DB | Total number of double bonds. | Goslin | v | v |
| Fatty acid properties | Total.OH | Total number of hydroxyl groups. | Goslin | v | v |
| Fatty acid properties | FA | Specification of fatty acid chains. | Goslin | v | v |
| Fatty acid properties | FA.C | The count of chain lengths in each specific chain. | Goslin | v | v |
| Fatty acid properties | FA.DB | The count of double bonds in each specific chain. | Goslin | v | v |
| Fatty acid properties | FA.OH | The count of hydroxyl groups in each specific chain. | Goslin | v | v |
| Lipid classification | Category | Category in the LIPIDMAPS classification system. | LION | v | v |
| Lipid classification | Main.Class | Main class in the LIPIDMAPS classification system. | LION | v | v |
| Lipid classification | Sub.Class | Sub class in the LIPIDMAPS classification system. | LION | v | v |
| Cellular component | Cellular.Component | The predominant organellar localization of lipids. | LION | v | v |
| Function | Function | The biological functions of lipids. | LION | v | v |
| Physical or chemical properties | Bond.type | The types of chemical bonds in lipids. | LION | v | v |
| Physical or chemical properties | Headgroup.Charge | The net electric charge of the lipid head group. | LION | v | v |
| Physical or chemical properties | Lateral.Diffusion | The lateral movement of lipids. | LION | v | v |
| Physical or chemical properties | Bilayer.Thickness | The thickness of a lipid bilayer. | LION | v | v |
| Physical or chemical properties | Intrinsic.Curvature | The intrinsic or spontaneous curvature of lipids. | LION | v | v |
| Physical or chemical properties | Transition.Temperature | The temperature at which a lipid undergoes a phase transition from a more ordered state (gel phase) to a more disordered state (liquid-crystalline phase), or vice versa. | LION | v | v |
| Fatty acid properties | FA.Unsaturation.Category1 | Fatty acids with <2 double bonds or >=2 double bonds. | LION | v | v |
| Fatty acid properties | FA.Unsaturation.Category2 | Fatty acids with 0, 1, 2, >2 or >5 double bonds. | LION | v | v |
| Fatty acid properties | FA.Chain.Length.Category1 | Fatty acids with <=18 carbons or >18 carbons. | LION | v | v |
| Fatty acid properties | FA.Chain.Length.Category2 | Fatty acids with <13, 13~15, 16~18, 19~21, 22~24 or >24 carbons. | LION | v | v |
| Fatty acid properties | FA.Chain.Length.Category3 | Fatty acids with 2~6 (short-chain), 7~12 (median-chain), 13~21 (long-chain) or >21 (very long-chain) carbons. | J Biochem. 2012 Nov;152(5):387-95., J Lipid Res. 2016 Jun;57(6):943-54. | v | v |
| Specific ratios | Chains Ether/Ester linked ratio | Assessing the frequency of ether-linked chains within different lipid classes. | LipidOne | v | |
| Specific ratios | Chains odd/even ratio | Evaluating the odd/even chain ratio across various lipid classes. | LipidOne | v | |
| Specific ratios | Ratio of Lysophospholipids to Phospholipids | The ratio of lysophospholipids to phospholipids, encompassing both total phospholipids and each individual phospholipid. | J Clin Invest. 2021 Apr 15;131(8):e135963. | v | |
| Specific ratios | Ratio of specific lipid class A to lipid class B | The ratio of PC/PE and TG/DG. | Dev Cell. 2018 May 21;45(4):481-495.e8., Hepatology. 2007 Oct;46(4):1081-90. | v |
FAQ 12: What formats should lipid names (features) adhere to for analysis?
-
We are integrating Goslin [1] for recognizing lipid shorthand notations, which supports various lipid dialects including LIPID MAPS, SwissLipids, HMDB, and IUPAC-IUB nomenclature for fatty acyl chains. Goslin accommodates lipid shorthand notations ranging from low-resolution levels, like species-level (sum composition), to high-resolution levels, such as isomeric subspecies-level (complete structure). Some examples of lipid shorthand notations are provided below:

-
Lipid shorthand notations follow specific conventions, beginning with the class abbreviation and specifying carbon atoms and double bond equivalents (C-atoms: DBE), e.g., TG 46:1. The number of oxygen-atoms or functional groups is separated by a semi-colon, e.g., C-atoms:DBE;O. You can access all supported lipid classes by Goslin 2.0 at the bottom.
-
Fatty acid chain positions are indicated by hyphens for known positions and underscores for unknown positions. For example, the lipid shorthand of 1-tetradecanoyl-2-hexadecanoyl-3-(9Z-hexadecenoyl)-sn-glycerol might be written as TG 14:0/16:0/16:1 (known positions) or TG 14:0_16:0_16:1 (unknown positions).
-
Double bond positions can be denoted using Δ-nomenclature or by specifying the number followed by the geometry (Z for cis, E for trans), as demonstrated in TG 14:0/16:0/16:1(9Z).
-
Additional notes:
-
Multiple lipid names on the same row: Sometimes, a lipid name may contain multiple lipid names separated by a "|". For instance, "TG 46:1|TG 14:0_16:0_16:1". Please remove one of the names to ensure clarity. In this case, you can change it to "TG 14:0_16:0_16:1".
-
Remove special markers: For structural isomers (i.e., lipids with the same annotation), annotate the end of the name with an ‘_A’, ‘_B’, etc. For example, "LPC 16:0_A" and "LPC 16:0_B" may not be recognized, please remove the ‘_A’, ‘_B’ labels.
-
Correct lipid class name: Full lipid class names are not accepted. For example, "Sphingomyelin(d18:1/24:1)" should be changed to "SM(d18:1/24:1)".
-
Insufficient resolution in fatty acid chains: Fatty acid chains that lack sufficient resolution are not accepted. For example, "TG 16:0;0_34:3;0" should be updated to reflect a proper name like "TG 50:3" for analysis.
-
Functional groups with oxygen atoms: When handling lipids with multiple oxygen-atom functional groups, position the oxygen-atom functional group before the number. For example, "SM 18:1;2O/16:0" should be modified to "SM 18:1;O2/16:0".
-
Functional group notation: For easier recognition, adjust the notation for functional groups like “(2OH)” to “O”. For example, "HexCer 20:0;O3/17:2;(2OH)" should be modified to "HexCer 20:0;O3/17:2;O".
-
Adhering to these formats ensures consistency and accuracy in lipid name representation for analysis purposes.
-
[1] Kopczynski D, Hoffmann N, Peng B, Liebisch G, Spener F, Ahrends R. Goslin 2.0 Implements the Recent Lipid Shorthand Nomenclature for MS-Derived Lipid Structures. Anal Chem. 2022 Apr 26;94(16):6097-6101.

- Multiple lipid names on the same row: Sometimes, a lipid name may contain multiple lipid names separated by a "|". For instance, "TG 46:1|TG 14:0_16:0_16:1". Please remove one of the names to ensure clarity. In this case, you can change it to "TG 14:0_16:0_16:1".
- Remove special markers: For structural isomers (i.e., lipids with the same annotation), annotate the end of the name with an ‘_A’, ‘_B’, etc. For example, "LPC 16:0_A" and "LPC 16:0_B" may not be recognized, please remove the ‘_A’, ‘_B’ labels.
- Correct lipid class name: Full lipid class names are not accepted. For example, "Sphingomyelin(d18:1/24:1)" should be changed to "SM(d18:1/24:1)".
- Insufficient resolution in fatty acid chains: Fatty acid chains that lack sufficient resolution are not accepted. For example, "TG 16:0;0_34:3;0" should be updated to reflect a proper name like "TG 50:3" for analysis.
- Functional groups with oxygen atoms: When handling lipids with multiple oxygen-atom functional groups, position the oxygen-atom functional group before the number. For example, "SM 18:1;2O/16:0" should be modified to "SM 18:1;O2/16:0".
- Functional group notation: For easier recognition, adjust the notation for functional groups like “(2OH)” to “O”. For example, "HexCer 20:0;O3/17:2;(2OH)" should be modified to "HexCer 20:0;O3/17:2;O".
FAQ 13: How to choose the appropriate data processing method? What do these methods perform?
-
In the data processing section for profiling, differential expression, machine learning, and correlation analysis, users can select missing values, sample normalization, and data transformation methods.
We provide detailed descriptions of each method to assist users in making appropriate choices.
| Aspect | Methods | Usage | Ref. |
|---|---|---|---|
| Missing values | Remove features with > 70% missing values (default threshold) | When the integrity of the dataset is paramount, removing features with a high proportion of missing values ensures that the analysis is based on more complete and reliable data. This step reduces the potential noise and bias that could be introduced by imputing a large amount of missing data for those features. For statistical analyses that require complete or near-complete data, such as multivariate analysis, correlation studies, or regression modeling, removing features with excessive missingness helps maintain the analysis's robustness. It prevents the undue influence of imputed values, which might not accurately represent the actual biological variation. | |
| Missing values | Replace with half of the minimum positive values in the original data (default threshold) | For lipid species that are known to be present in the sample but are at concentrations too low for accurate quantification, this imputation method allows for their inclusion in the analysis without artificially inflating their estimated concentrations. This can be particularly important in studies focusing on trace lipids or in comparative analyses where the presence/absence of certain lipids may be significant. | (1) |
| Missing values | Replace by mean | When the lipid concentrations across samples are approximately normally distributed without significant skewness or outliers, replacing missing values with the mean provides a reasonable estimate that maintains the overall distributional characteristics of the data. | (1) |
| Missing values | Replace by median | In lipidomics datasets where the distribution of lipid concentrations is skewed or non-normal, replacing missing values with the median is preferred over the mean. The median is less sensitive to outliers and extreme values, providing a more representative central tendency measure for skewed data. | (1) |
| Missing values | Quantile Regression Imputation of Left-Censored data (QRILC) | QRILC is a statistical method designed to handle left-censored data where observations are below measuring instruments' detecting concentrations or sensitivity threshold. This approach helps to provide a more accurate statistical analysis of the entire dataset by preserving its distributional characteristics and dealing with extreme values and asymmetric distributions. | (2) |
| Missing values | Singular Value Decomposition | When the objective is to uncover and utilize latent patterns within the lipidomics data for imputation, SVD provides a mathematical framework. SVD can capture these relationships in its decomposition, enabling a more nuanced approach to imputation that considers the multivariate structure of the data. | (1) |
| Missing values | K-Nearest Neighbours | When the dataset has a moderate to low level of missing data, KNN imputation can be effectively applied. The method requires enough complete or nearly complete cases to find neighbors with similar profiles for accurate imputation. KNN is particularly effective when missing values are randomly distributed across the dataset. The method relies on the premise that the pattern of missingness is not systematic but random. | (1) |
| Missing values | IRMI: The Iterative Robust Model-based Imputation | IRMI is designed to be an efficient and robust approach for imputing missing values, especially when dealing with datasets with outliers or irregular distributions. It is particularly useful in complex datasets where missing data are not random and might depend on other variables in the dataset. | (3) |
| Missing values | Probabilistic principal component analysis | PPCA can effectively handle dimensionality, providing a principled way to estimate missing values by capturing the major trends and patterns in the data. It models the underlying structure of the data, using a probabilistic framework to estimate missing values, making it well-suited for datasets where the relationships among variables are not straightforward. | (1) |
| Missing values | Principal Component Analysis | PCA-based imputation is most suitable for datasets where the level of missingness is not overwhelmingly high. This approach assumes that the observed data can represent the dataset's underlying structure well enough to predict missing values accurately. PCA for missing value imputation is most effective when missing values occur randomly. | (1) |
| Sample normalization | Percentage | In experiments where variations in sample volume, concentration, or extraction efficiency are expected, percentage normalization compensates for these variations. By converting lipid concentrations to percentages, the method ensures that the analysis reflects differences in lipid composition, independent of the total amount of lipids extracted. | |
| Sample normalization | Perform Probabilistic Quotient Normalization (PQN) | PQN is designed to correct for multiplicative (i.e., proportional) variations across samples, such as those due to differences in dilution, concentration, or volume. It is not intended to correct additive errors or biases. | (4) |
| Sample normalization | Normalization by sum | When the objective is to compare lipid profiles across various samples, normalization by sum ensures that differences in lipid concentrations are not merely due to variations in the total lipid content of the samples. By normalizing to the total sum, each sample is adjusted to have the same total lipid content, allowing for meaningful comparisons of individual lipid species relative abundances. In studies where lipidomics data are collected in multiple batches or from different platforms, resulting in systematic variations, normalization by sum can help mitigate these batch effects by standardizing the total lipid content across all batches. This is crucial for integrating data cohesively and ensuring that observed differences are due to biological variability rather than technical discrepancies. | (1) |
| Sample normalization | Normalization by median | When the distribution of lipid concentrations across samples is skewed, normalization by median can help mitigate the influence of extreme values or outliers. The median provides a more robust central tendency measure, making it suitable for datasets with skewed distributions. | (1) |
| Sample normalization | Quantile normalization (suggested only for > 1000 features) | Quantile normalization is utilized when systematic biases across samples that may arise from differences in sample preparation, handling, or measurement technologies need to be corrected. This normalization ensures that the overall distribution of lipid concentrations is consistent across samples, making them directly comparable. In studies comparing lipid profiles across different conditions, treatments, or time points, quantile normalization helps minimize the impact of technical variability. | (1) |
| Sample normalization | Mean centering | Mean centering is used when the objective is to emphasize the variability of each lipid species relative to the average behavior within the dataset. | (1) |
| Sample normalization | Auto scaling (mean-centered and divided by the standard deviation of each variable) | Auto-scaling is applied when variables within the dataset span different units of measurement or magnitudes, making them incomparable. By standardizing, all variables are brought to a common scale with a mean of 0 and a standard deviation of 1, facilitating direct comparisons across variables. | (1) |
| Sample normalization | Pareto scaling (mean-centered and divided by the square root of the standard deviation of each variable) | Pareto scaling is a preprocessing technique used in lipidomics data analysis under specific conditions that require a balance between retaining the data's original structure and reducing the influence of high-magnitude variables. It is chosen when an intermediate scaling level is needed between no scaling and auto-scaling | (1) |
| Sample normalization | Range scaling (mean-centered and divided by the range of each variable) | When the analysis involves comparing measurements across different lipid species that may have vastly different ranges of concentrations, range scaling ensures that all variables contribute equally to the analysis. When the goal is to highlight relative changes across samples rather than absolute concentrations, range scaling allows for identifying patterns that are not biased by the absolute magnitude of the measurements. | (1) |
| Sample normalization | Variance Stabilizing Transformation (VAST) scaling | The technique is most applicable when the data exhibit heteroscedasticity, meaning the variance differs across the range of data. VAST scaling is ideal for studies that involve comparisons across multiple groups or conditions, as it ensures that the variance within features does not unduly influence the results. | (5) |
| Sample normalization | Level scaling | It aims to adjust the measurements to be on a similar scale or magnitude. In datasets where some features have much higher magnitudes or values than others, scaling ensures that all features have an equal opportunity to influence the analysis, thereby preventing the analysis from being skewed towards high-magnitude features. | (5) |
| Data transformation | Log10 transformation | This transformation is particularly beneficial in Lipidomics data, which often exhibit non-normal (skewed) distributions due to the wide range of concentrations across different lipid species. It helps normalize the data, making it more suitable for statistical analyses that assume normality. | (1) |
| Data transformation | Square root transformation | The transformation is less drastic than logging, making it suitable for datasets where the dynamic range is not extremely wide but still presents heteroscedasticity. | (1) |
| Data transformation | Cube root transformation | For lipidomics data exhibiting slight to moderate skewness, the cube root transformation can effectively normalize distributions, making it a preferable choice when data do not require the more substantial impact of log or square root transformations. | (1) |
-
Chong, J. and Xia, J. (2018) MetaboAnalystR: an R package for flexible and reproducible analysis of metabolomics data. Bioinformatics, 34, 4313-4314.
http://www.ncbi.nlm.nih.gov/pubmed/29955821
http://dx.doi.org/10.1093/bioinformatics/bty528 -
Wei, R., Wang, J., Su, M., Jia, E., Chen, S., Chen, T. and Ni, Y. (2018) Missing Value Imputation Approach for Mass Spectrometry-based Metabolomics Data. Sci Rep, 8, 663.
http://www.ncbi.nlm.nih.gov/pubmed/29330539
http://dx.doi.org/10.1038/s41598-017-19120-0 -
Templ, M., Kowarik, A. and Filzmoser, P. (2011) Iterative stepwise regression imputation using standard and robust methods. Computational Statistics & Data Analysis, 55, 2793-2806.
http://dx.doi.org/https://doi.org/10.1016/j.csda.2011.04.012 -
Dieterle, F., Ross, A., Schlotterbeck, G. and Senn, H. (2006) Probabilistic quotient normalization as robust method to account for dilution of complex biological mixtures. Application in 1H NMR metabonomics. Anal Chem, 78, 4281-4290.
http://www.ncbi.nlm.nih.gov/pubmed/16808434
http://dx.doi.org/10.1021/ac051632c -
van den Berg, R.A., Hoefsloot, H.C., Westerhuis, J.A., Smilde, A.K. and van der Werf, M.J. (2006) Centering, scaling, and transformations: improving the biological information content of metabolomics data. BMC Genomics, 7, 142.
http://www.ncbi.nlm.nih.gov/pubmed/16762068
http://dx.doi.org/10.1186/1471-2164-7-142
FAQ 14: What is the version of all the R packages used in LipidSig2.0?
-
The versions of all R packages utilized in LipidSig2.0 are detailed in the following table.
Package
Version
base
4.2.3
dplyr
1.1.3
tibble
3.2.1
purrr
1.0.2
shiny
1.7.5
gatom
0.99.3
scales
1.2.1
visNetwork
2.1.2
igraph
1.5.1
data.table
1.14.8
tidyr
1.3.0
ggplot2
3.4.3
ggthemes
4.2.4
ggpubr
0.6.0
hwordcloud
0.1.0
wordcloud
2.6
broom
1.0.5
stats
4.2.3
stringr
1.5.0
plotly
4.10.2
rstatix
0.7.2
S4Vectors
0.36.2
grDevices
4.2.3
iheatmapr
0.7.0
SummarizedExperiment
1.28.0
readxl
1.4.3
dbscan
1.1.11
factoextra
1.0.7
Rtsne
0.16
uwot
0.1.16
mixOmics
6.22.0
tidyselect
1.2.0
Hmisc
5.1.1
pcaMethods
1.90.0
preprocessCore
1.60.2
imputeLCMD
2.1
fgsea
1.24.0
reshape2
1.4.4
| Package | Version |
|---|---|
| base | 4.2.3 |
| dplyr | 1.1.3 |
| tibble | 3.2.1 |
| purrr | 1.0.2 |
| shiny | 1.7.5 |
| gatom | 0.99.3 |
| scales | 1.2.1 |
| visNetwork | 2.1.2 |
| igraph | 1.5.1 |
| data.table | 1.14.8 |
| tidyr | 1.3.0 |
| ggplot2 | 3.4.3 |
| ggthemes | 4.2.4 |
| ggpubr | 0.6.0 |
| hwordcloud | 0.1.0 |
| wordcloud | 2.6 |
| broom | 1.0.5 |
| stats | 4.2.3 |
| stringr | 1.5.0 |
| plotly | 4.10.2 |
| rstatix | 0.7.2 |
| S4Vectors | 0.36.2 |
| grDevices | 4.2.3 |
| iheatmapr | 0.7.0 |
| SummarizedExperiment | 1.28.0 |
| readxl | 1.4.3 |
| dbscan | 1.1.11 |
| factoextra | 1.0.7 |
| Rtsne | 0.16 |
| uwot | 0.1.16 |
| mixOmics | 6.22.0 |
| tidyselect | 1.2.0 |
| Hmisc | 5.1.1 |
| pcaMethods | 1.90.0 |
| preprocessCore | 1.60.2 |
| imputeLCMD | 2.1 |
| fgsea | 1.24.0 |
| reshape2 | 1.4.4 |
FAQ 15: Data Privacy Policy for LipidSig 2.0
- Data Processing and Retention
- Data Upload and Processing:
- All user data uploaded to LipidSig 2.0 is processed exclusively within the Random Access Memory (RAM) of our system.
- Data processing commences at the initiation of each user session.
- Data Deletion:
- Upon termination of the user session, all uploaded and processed data is permanently and irrevocably deleted from the system's RAM.
- No residual user data persists beyond the duration of the active session.
- Data Upload and Processing:
- Data Storage Policy
- Absence of Persistent Storage:
- LipidSig 2.0 does not implement any "save to disk" processes throughout the entire data processing lifecycle.
- No user data is stored on permanent storage media, including but not limited to hard drives, solid-state drives, or any other form of non-volatile memory.
- Absence of Persistent Storage:
- Data Sharing and Third-Party Involvement
- Exclusive Processing:
- All data processing activities are conducted solely within the confines of a dedicated server located at China Medical University.
- No user data is shared, transmitted, or made accessible to any third parties under any circumstances.
- Absence of Third-Party Processing:
- LipidSig 2.0 does not engage or contract any external entities for data processing purposes.
- All computational and analytical processes are performed exclusively by our internal systems.
- Exclusive Processing:
- Data Transfer
- No Data Transfer:
- LipidSig 2.0 does not transfer user data to any external systems, servers, or locations.
- All data remains within the original processing environment for the duration of its existence (i.e., the user session).
- No Data Transfer:
- Security Measures
- Isolated Environment:
- The server hosting LipidSig 2.0 operates in an isolated environment to prevent unauthorized access or data interception.
- Session Isolation:
- Each user session is isolated to ensure that data from different sessions cannot intermingle or be accessed across sessions.
- Isolated Environment:
- User Rights and Responsibilities
- Data Control:
- Users retain full control over their data for the duration of their session.
- Users are responsible for maintaining the confidentiality of any sensitive information they choose to upload.
- Data Control:
- Policy Updates
- Notification of Changes:
- Any modifications to this privacy policy will be prominently displayed on the LipidSig 2.0 platform.
- Users are encouraged to review this policy periodically for any updates or changes.
- Notification of Changes:
- Contact Information
For any questions or concerns regarding this privacy policy, please contact:
Wei-Chung Cheng, Ph.D.
Professor
Program for Cancer Molecular Biology and Drug Discovery
College of Medicine
China Medical University
Taichung 404, Taiwan
Tel: +886-4-22053366 ext. 7929
Email: wccheng@mail.cmu.edu.tw
Last Updated: 2024.10.10